遗传算法 python
代码:
import numpy as np
# ---------------定义目标函数-------------------
def f(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
-x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
# ---------------DNA解码(计算x,y)-------------
def translate_DNA(animal): # 解码种群的DNA
def DNA2t10(DNA): # 带x, y范围的转换
# pop: (POP_SIZE, DNA_SIZE) * (DNA_SIZE, 1) --> (POP_SIZE, 1)完成解码
DNA = np.expand_dims(DNA, 0)
y = DNA.dot(2 ** np.arange(DNA_bit)[::-1]) / float(2 ** DNA_bit - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return y
DNA_result = []
for i in range(0, DNA_bit * DNA_num, DNA_bit):
DNA = animal[i:i + DNA_bit]
translated_DNA = DNA2t10(DNA)
DNA_result.append(translated_DNA)
return DNA_result
# ------------------计算适应度(计算误差,考虑定义域)------------
def get_fitness(animals): # 计算种群各个部分的适应度
fitness_score = np.zeros(len(animals))
for i in range(len(animals)):
x, y = translate_DNA(animals[i])
fitness_score[i] = f(x, y)
fitness_score = (fitness_score - np.min(fitness_score)) + 1e-5
return fitness_score
# -------------适者生存(挑选误差较小的答案)---------------
# 根据之前的适应度的结果,误差越小适应度大,可以转换为概率,因此被留下的概率也就越大。
# 轮盘赌法
def select_animal(animals, fitness): # 按照适应度选择留下的种群
idx = np.random.choice(np.arange(animal_num), size=animal_num, replace=True, p=(fitness) / (fitness.sum() + 1e-8))
return animals[idx]
# -----生殖、变异(更改部分二进制位,取反部分二进制位,可能生成误差更小的答案)--------
def variation(children, variation_rate, per_gene_variation=True): # 模拟编译
"""
Args:
children: 交叉后的基因
variation_rate: 突变概率
per_gene_variation: 是否逐个基因点突变
Returns:
"""
if per_gene_variation:
gene_size = len(children)
for i in range(gene_size):
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
children[i] = children[i] ^ 1 # 这一位取反
return children
else:
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_bit * 2) # 随机产生一个实数,代表要变异基因的位置
children[mutate_point] = children[mutate_point] ^ 1 # 这一位取反
return children
def crossover_and_variation(animals, cross_rate, is_randomise=True): # 模拟生殖过程(包括交配和变异)
new_animals = []
for father in animals:
child = father # 选择父亲
if np.random.rand() < cross_rate: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = animals[np.random.randint(animal_num)] # 再选择母亲
if is_randomise:
cross_points = np.random.randint(low=0, high=2, size=DNA_bit * DNA_num) # 随机产生交叉的点
index = np.argwhere(cross_points == 1) # 找到交叉点
child[index] = mother[index] # 交叉互换,模拟生殖
else:
cross_points = np.random.randint(low=0, high=DNA_bit * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
variation(child, variation_rate) # 变异
new_animals.append(child)
return np.array(new_animals)
def get_result(animals): # 获取结果
fitness = get_fitness(animals)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translate_DNA(animals[max_fitness_index])
print("最优的基因型:", animals[max_fitness_index])
print("x: {} y: {} 函数值: {}".format(x, y, f(x, y)))
return
if __name__ == '__main__':
# -----------初始化参数-----------------
DNA_bit = 13 # 一个DNA的二进制位数,(第一维表示符号位)
Int_bit = 2 # DNA_bit-1(符号位bit)之后整数占的bit位
DNA_num = 2 # DNA的个数
animal_num = 200 # 开始种群的数量
cross_rate = 0.8 # 生殖交叉概率
variation_rate = 0.005 # 变异的概率
generator_n = 50 # 种群演变的次数
X_BOUND = [-3, 3] # x取值范围
Y_BOUND = [-3, 3] # y取值范围
# 初始化种群,需要判断开始的种群是否符合值域
animals = np.array([np.random.randint(0, 2, size=(DNA_bit * DNA_num)) for i in range(animal_num)])
# 模拟进化选择generator_n轮
for i in range(generator_n):
fitness_score = get_fitness(animals)
selected_animals = select_animal(animals, fitness_score)
animals = crossover_and_variation(selected_animals, cross_rate)
print("第 {} 次迭代".format(i))
get_result(animals)带交互模式的代码:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
# ---------------定义目标函数-------------------
def f(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
-x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
# ---------------DNA解码(计算x,y)-------------
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, 1::2] # 奇数列表示X
y_pop = pop[:, ::2] # 偶数列表示y
# pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x = x_pop.dot(2 ** np.arange(DNA_bit)[::-1]) / float(2 ** DNA_bit - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
y = y_pop.dot(2 ** np.arange(DNA_bit)[::-1]) / float(2 ** DNA_bit - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return x, y
# ------------------计算适应度(计算误差,考虑定义域)------------
def get_fitness(pop):
x, y = translateDNA(pop)
pred = f(x, y)
# 减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],
# 最后在加上一个很小的数防止出现为0的适应度
return (pred - np.min(pred)) + 1e-5
# -------------适者生存(挑选误差较小的答案)---------------
# 根据之前的适应度的结果,误差越小适应度大,可以转换为概率,因此被留下的概率也就越大。
# 轮盘赌法
def select_animal(animals, fitness): # 按照适应度选择留下的种群
idx = np.random.choice(np.arange(animal_num), size=animal_num, replace=True, p=(fitness) / (fitness.sum() + 1e-8))
return animals[idx]
# -----生殖、变异(更改部分二进制位,取反部分二进制位,可能生成误差更小的答案)--------
def variation(children, variation_rate, per_gene_variation=True): # 模拟编译
"""
Args:
children: 交叉后的基因
variation_rate: 突变概率
per_gene_variation: 是否逐个基因点突变
Returns:
"""
if per_gene_variation:
gene_size = len(children)
for i in range(gene_size):
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
children[i] = children[i] ^ 1 # 这一位取反
return children
else:
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_bit * 2) # 随机产生一个实数,代表要变异基因的位置
children[mutate_point] = children[mutate_point] ^ 1 # 这一位取反
return children
def crossover_and_variation(animals, cross_rate, is_randomise=True): # 模拟生殖过程(包括交配和变异)
new_animals = []
for father in animals:
child = father # 选择父亲
if np.random.rand() < cross_rate: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = animals[np.random.randint(animal_num)] # 再选择母亲
if is_randomise:
cross_points = np.random.randint(low=0, high=2, size=DNA_bit * DNA_num) # 随机产生交叉的点
index = np.argwhere(cross_points == 1) # 找到交叉点
child[index] = mother[index] # 交叉互换,模拟生殖
else:
cross_points = np.random.randint(low=0, high=DNA_bit * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
variation(child, variation_rate) # 变异
new_animals.append(child)
return np.array(new_animals)
def get_result(animals): # 获取结果
fitness = get_fitness(animals)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translateDNA(animals)
x, y = x[max_fitness_index], y[max_fitness_index]
print("最优的基因型:", animals[max_fitness_index])
print("x: {} y: {} 函数值: {}".format(x, y, f(x, y)))
return
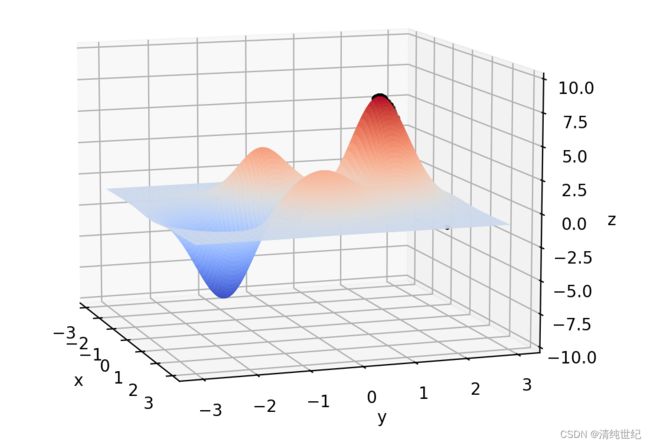
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X,Y = np.meshgrid(X, Y)
Z = f(X, Y)
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
ax.set_zlim(-10,10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(1)
plt.show()
if __name__ == '__main__':
# -----------初始化参数-----------------
DNA_bit = 13 # 一个DNA的二进制位数,(第一维表示符号位)
Int_bit = 2 # DNA_bit-1(符号位bit)之后整数占的bit位
DNA_num = 2 # DNA的个数
animal_num = 200 # 开始种群的数量
cross_rate = 0.8 # 生殖交叉概率
variation_rate = 0.005 # 变异的概率
generator_n = 200 # 种群演变的次数
X_BOUND = [-3, 3] # x取值范围
Y_BOUND = [-3, 3] # y取值范围
# 初始化种群,需要判断开始的种群是否符合值域
animals = np.random.randint(0, 2, size=(animal_num, DNA_bit * DNA_num))
# ----------------绘图-----------
fig = plt.figure()
ax = Axes3D(fig)
plt.ion() # 将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
# 模拟进化选择generator_n轮
for i in range(generator_n):
x, y = translateDNA(animals)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, f(x, y), c='black', marker='.')
plt.show()
plt.pause(0.1)
fitness_score = get_fitness(animals)
selected_animals = select_animal(animals, fitness_score)
animals = crossover_and_variation(selected_animals, cross_rate)
print("第 {} 次迭代".format(i))
get_result(animals)
plt.ioff()
plot_3d(ax)输出所有迭代中最优值代码:
import numpy as np
# ---------------定义目标函数-------------------
def f(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
-x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
# ---------------DNA解码(计算x,y)-------------
def translate_DNA(animal): # 解码种群的DNA
def DNA2t10(DNA): # 带x, y范围的转换
# pop: (POP_SIZE, DNA_SIZE) * (DNA_SIZE, 1) --> (POP_SIZE, 1)完成解码
DNA = np.expand_dims(DNA, 0)
y = DNA.dot(2 ** np.arange(DNA_bit)[::-1]) / float(2 ** DNA_bit - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return y
DNA_result = []
for i in range(0, DNA_bit * DNA_num, DNA_bit):
DNA = animal[i:i + DNA_bit]
translated_DNA = DNA2t10(DNA)
DNA_result.append(translated_DNA)
return DNA_result
# ------------------计算适应度(计算误差,考虑定义域)------------
def get_fitness(animals): # 计算种群各个部分的适应度
fitness_score = np.zeros(len(animals))
for i in range(len(animals)):
x, y = translate_DNA(animals[i])
fitness_score[i] = f(x, y)
fitness_score = (fitness_score - np.min(fitness_score)) + 1e-5
return fitness_score
# -------------适者生存(挑选误差较小的答案)---------------
# 根据之前的适应度的结果,误差越小适应度大,可以转换为概率,因此被留下的概率也就越大。
# 轮盘赌法
def select_animal(animals, fitness): # 按照适应度选择留下的种群
idx = np.random.choice(np.arange(animal_num), size=animal_num, replace=True, p=(fitness) / (fitness.sum() + 1e-8))
return animals[idx]
# -----生殖、变异(更改部分二进制位,取反部分二进制位,可能生成误差更小的答案)--------
def variation(children, variation_rate, per_gene_variation=True): # 模拟编译
"""
Args:
children: 交叉后的基因
variation_rate: 突变概率
per_gene_variation: 是否逐个基因点突变
Returns:
"""
if per_gene_variation:
gene_size = len(children)
for i in range(gene_size):
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
children[i] = children[i] ^ 1 # 这一位取反
return children
else:
if np.random.rand() < variation_rate: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_bit * 2) # 随机产生一个实数,代表要变异基因的位置
children[mutate_point] = children[mutate_point] ^ 1 # 这一位取反
return children
def crossover_and_variation(animals, cross_rate, is_randomise=True): # 模拟生殖过程(包括交配和变异)
new_animals = []
for father in animals:
child = father # 选择父亲
if np.random.rand() < cross_rate: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = animals[np.random.randint(animal_num)] # 再选择母亲
if is_randomise:
cross_points = np.random.randint(low=0, high=2, size=DNA_bit * DNA_num) # 随机产生交叉的点
index = np.argwhere(cross_points == 1) # 找到交叉点
child[index] = mother[index] # 交叉互换,模拟生殖
else:
cross_points = np.random.randint(low=0, high=DNA_bit * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
variation(child, variation_rate) # 变异
new_animals.append(child)
return np.array(new_animals)
def get_result(animals): # 获取结果
fitness = get_fitness(animals)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translate_DNA(animals[max_fitness_index])
print("最优的基因型:", animals[max_fitness_index])
print("x: {} y: {} 函数值: {}".format(x, y, f(x, y)))
return f(x, y), animals[max_fitness_index]
if __name__ == '__main__':
# -----------初始化参数-----------------
np.random.seed(0)
DNA_bit = 13 # 一个DNA的二进制位数,(第一维表示符号位)
Int_bit = 2 # DNA_bit-1(符号位bit)之后整数占的bit位
DNA_num = 2 # DNA的个数
animal_num = 200 # 开始种群的数量
cross_rate = 0.8 # 生殖交叉概率
variation_rate = 0.005 # 变异的概率
generator_n = 50 # 种群演变的次数
X_BOUND = [-3, 3] # x取值范围
Y_BOUND = [-3, 3] # y取值范围
best = {}
index = []
# 初始化种群,需要判断开始的种群是否符合值域
animals = np.array([np.random.randint(0, 2, size=(DNA_bit * DNA_num)) for i in range(animal_num)])
# 模拟进化选择generator_n轮
for i in range(generator_n):
fitness_score = get_fitness(animals)
selected_animals = select_animal(animals, fitness_score)
animals = crossover_and_variation(selected_animals, cross_rate)
print("第 {} 次迭代".format(i))
va,ind = get_result(animals)
best[i] = ind
index.append(va)
inde = np.argmax(np.array(index))
print("函数最大值:",index[inde], "该值下最优基因:",best[inde])附录:适应度
假设求函数最大值。在选择过程中需要根据个体适应度确定每个个体被保留下来的概率,而概率不能是负值,所以减去预测中的最小值把适应度值的最小区间提升到从0开始,但是如果适应度为0,其对应的概率也为0,表示该个体不可能在选择中保留下来,这不符合算法思想,遗传算法不绝对否定谁也不绝对肯定谁,所以最后加上了一个很小的正数。代码如下:
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return -(pred - np.max(pred)) + 1e-3对此,最小值适应度函数类似。在求最小值问题上,函数值越小的可能解对应的适应度应该越大,同时适应度也不能为负值,先将适应度减去最大预测值,将适应度可能取值区间压缩为 [ n p . m i n ( p r e d ) − n p . m a x ( p r e d ) , 0 ] [np.min(pred)-np.max(pred), 0] [np.min(pred)−np.max(pred),0],然后添加个负号将适应度变为正数,同理为了不出现0,最后在加上一个很小的正数。代码如下:
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return -(pred - np.max(pred)) + 1e-3交叉和突变:
需要说明的是交叉和变异不是必然发生,而是有一定概率发生。先考虑交叉,最坏情况,交叉产生的子代的DNA都比父代要差(这样算法有可能朝着优化的反方向进行,不收敛),如果交叉是有一定概率不发生,那么就能保证子代有一部分基因和当前这一代基因水平一样;而变异本质上是让算法跳出局部最优解,如果变异时常发生,或发生概率太大,那么算法到了最优解时还会不稳定。交叉概率,范围一般是0.6~1,突变常数(又称为变异概率),通常是0.1或者更小。
2D的交互模式:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,6,200)
def f(x):
return np.sin(x)
plt.ion() # 开启交互模式
plt.show()
for i in range(10):
plt.cla() # 清除axes,即当前 figure 中的活动的axes,但其他axes保持不变。
index = np.argwhere(np.random.randint(0,2,200)==1)
y = x[index]
plt.plot(x, f(x))
plt.scatter(y,f(y))
plt.pause(0.1)
plt.ioff() # 关闭交互模式