使用遗传算法计算神经网络的超参数
遗传算法是基于种群的思想,将问题的解通过编码的方式转化为种群中的个体,并让这些个体不断地通过选择、交叉和变异算子模拟生物的进化过程,然后利用“优胜劣汰”法则选择种群中适应性较强的个体构成子种群,然后让子种群重复类似的进化过程,直到找到问题的最优解或者到达一定的进化(运算)时间。
个体(染色体):自然界中一个个体(染色体)代表一个生物,在GA算法中,个体(染色体)代表了具体问题的一个解。
基因:在GA算法中,基因代表了具体问题解的一个决策变量。
种群:多个个体即组成一个种群。GA算法中,一个问题的多组解即构成了问题的解的种群。
Step 1. 种群初始化。首先随机生成一些个体。然后通过编码的方式,编码为一个向量表示。这里是为了方便后面的种群的交叉变异。将个体(可能解)编码后的二进制串叫做染色体,染色体(或者有人叫DNA)就是个体(可能解)的二进制编码表示。
Step 2. 评估种群。利用启发式算法对种群中的个体(矩形件的排入顺序)生成排样图并依此计算个体的适应函数值(利用率),然后保存当前种群中的最优个体作为搜索到的最优解。
Step 3. 选择操作。根据种群中个体的适应度的大小,通过轮盘赌或者期望值方法,将适应度高的个体从当前种群中选择出来。
Step 4. 交叉操作。将上一步骤选择的个体,用一定的概率阀值Pc控制是否利用单点交叉、多点交叉或者其他交叉方式生成新的交叉个体。
Step 5. 变异操作。用一定的概率阀值Pm控制是否对个体的部分基因执行单点变异或多点变异。
Step 6. 终止判断。若满足终止条件,则终止算法,否则返回Step 2。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 4
POP_SIZE = 100
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 10
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]
def F(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
-x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X, Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_zlim(-10, 10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
def get_fitness(pop):
x, y = translateDNA(pop)
pred = F(x, y)
return (pred - np.min(
pred)) + 1e-3 # 减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, 1::2] # 奇数列表示X
y_pop = pop[:, ::2] # 偶数列表示y
# pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return x, y
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 2) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
if __name__ == "__main__":
fig = plt.figure()
ax = Axes3D(fig)
plt.ion() # 将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2)) # matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS): # 迭代N代
x, y = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, F(x, y), c='black', marker='o');
plt.show();
plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
# F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
fitness = get_fitness(pop)
pop = select(pop, fitness) # 选择生成新的种群
print_info(pop)
plt.ioff()
plot_3d(ax)
上面的代码来自:遗传算法详解 附python代码实现_重学CS的博客-CSDN博客_python遗传算法
用遗传算法来判断神经网络中的参数
网络结构
import torch
from sklearn import datasets
import torch.nn.functional as Fun
from torch import nn
# 2. 定义BP神经网络
class Net(torch.nn.Module):
def __init__(self, num,n_hidden,n_feature=4, n_output=3):
super(Net, self).__init__()
self.n_feature=n_feature
self.n_hidden=int(n_hidden) ##隐藏层神经元的个数
self.num=int(num) ###中间隐藏层的层数
self.input=torch.nn.Linear(n_feature,n_hidden)
self.hidden = self.make_layer(torch.nn.Linear,self.num) # 定义隐藏层网络
self.out = torch.nn.Linear(n_hidden, n_output) # 定义输出层网络
self.data,self.label=self.precess_data()
def make_layer(self, block, num_of_layer):
layers = []
for _ in range(num_of_layer):
layers.append(block(self.n_hidden,self.n_hidden))
return nn.Sequential(*layers)
def forward(self, x):
x = Fun.relu(self.input(x))# 隐藏层的激活函数,采用relu,也可以采用sigmod,tanh
x=Fun.relu(self.hidden(x))
x = self.out(x) # 输出层不用激活函数
return x
def precess_data(self):
# 1. 数据准备
dataset = datasets.load_iris()
data = torch.FloatTensor(dataset['data'])
label = torch.LongTensor(dataset['target'])
return data,label
def train(self):
# 3. 定义优化器损失函数
self.net = Net(num=self.num,n_hidden=self.n_hidden,n_feature=4, n_output=3) #n_feature:输入的特征维度,n_hiddenb:神经元个数,n_output:输出的类别个数
optimizer = torch.optim.SGD(self.net.parameters(), lr=0.02) # 优化器选用随机梯度下降方式
loss_func = torch.nn.CrossEntropyLoss() # 对于多分类一般采用的交叉熵损失函数,
# 4. 训练数据
for t in range(500):
out = self.net(self.data) # 输入data,输出out
loss = loss_func(out, self.label) # 输出与label对比
optimizer.zero_grad() # 梯度清零
loss.backward() # 前馈操作
optimizer.step() # 使用梯度优化器
# 5. 得出结果
def test(self):
self.train()
out = self.net(self.data) #out是一个计算矩阵,可以用Fun.softmax(out)转化为概率矩阵
prediction = torch.max(out, 1)[1] # 返回index 0返回原值
pred_y = prediction.data.numpy()
target_y = self.label.data.numpy()
# 6.衡量准确率
accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
# print("莺尾花预测准确率",accuracy)
return accuracy这里我们需要调节的参数是神经网络隐藏层个数,和隐藏层神经元个数。
因为这里两个变量都是整数,所以不可以用上文例子中的编码和解码方法。这里我们使用的是将一个二进制转换为十进制进行解码。
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, :2]
y_pop = pop[:, 2:]
# 解码 将一个个体解码为一个解
x=np.sum(np.power(2, np.arange(x_pop.shape[-1] - 1, -1, -1)) * x_pop, axis=1).reshape((-1, 1))
y = np.sum(np.power(2, np.arange(y_pop.shape[-1] - 1, -1, -1)) * y_pop, axis=1).reshape((-1, 1))
return x, y完整代码
import torch
from sklearn import datasets
import torch.nn.functional as Fun
from torch import nn
import numpy as np
from matplotlib import pyplot as plt
DNA_SIZE = 4
POP_SIZE = 20
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 5
num = [0, 4] ##2**2
n_hidden = [0, 50] ##2**6
# 2. 定义BP神经网络
class Net(torch.nn.Module):
def __init__(self, num,n_hidden,n_feature=4, n_output=3):
super(Net, self).__init__()
self.n_feature=n_feature
self.n_hidden=int(n_hidden) ##隐藏层神经元的个数
self.num=int(num) ###中间隐藏层的层数
self.input=torch.nn.Linear(n_feature,n_hidden)
self.hidden = self.make_layer(torch.nn.Linear,self.num) # 定义隐藏层网络
self.out = torch.nn.Linear(n_hidden, n_output) # 定义输出层网络
self.data,self.label=self.precess_data()
def make_layer(self, block, num_of_layer):
layers = []
for _ in range(num_of_layer):
layers.append(block(self.n_hidden,self.n_hidden))
return nn.Sequential(*layers)
def forward(self, x):
x = Fun.relu(self.input(x))# 隐藏层的激活函数,采用relu,也可以采用sigmod,tanh
x=Fun.relu(self.hidden(x))
x = self.out(x) # 输出层不用激活函数
return x
def precess_data(self):
# 1. 数据准备
dataset = datasets.load_iris()
data = torch.FloatTensor(dataset['data'])
label = torch.LongTensor(dataset['target'])
return data,label
def train(self):
# 3. 定义优化器损失函数
self.net = Net(num=self.num,n_hidden=self.n_hidden,n_feature=4, n_output=3) #n_feature:输入的特征维度,n_hiddenb:神经元个数,n_output:输出的类别个数
optimizer = torch.optim.SGD(self.net.parameters(), lr=0.02) # 优化器选用随机梯度下降方式
loss_func = torch.nn.CrossEntropyLoss() # 对于多分类一般采用的交叉熵损失函数,
# 4. 训练数据
for t in range(500):
out = self.net(self.data) # 输入data,输出out
loss = loss_func(out, self.label) # 输出与label对比
optimizer.zero_grad() # 梯度清零
loss.backward() # 前馈操作
optimizer.step() # 使用梯度优化器
# 5. 得出结果
def test(self):
self.train()
out = self.net(self.data) #out是一个计算矩阵,可以用Fun.softmax(out)转化为概率矩阵
prediction = torch.max(out, 1)[1] # 返回index 0返回原值
pred_y = prediction.data.numpy()
target_y = self.label.data.numpy()
# 6.衡量准确率
accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
# print("莺尾花预测准确率",accuracy)
return accuracy
def F(num, n_hidden):
accuracy=[]
for i in range(len(num)):
model=Net(int(num[i]),int(n_hidden[i]))
score=model.test()
accuracy.append(score)
return accuracy
def get_fitness(pop):
x, y = translateDNA(pop)
pred = F(x, y)
# 减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
return (pred - np.min(pred)) + 1e-3,pred
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, :2]
y_pop = pop[:, 2:]
# 解码 将一个个体解码为一个解
x=np.sum(np.power(2, np.arange(x_pop.shape[-1] - 1, -1, -1)) * x_pop, axis=1).reshape((-1, 1))
y = np.sum(np.power(2, np.arange(y_pop.shape[-1] - 1, -1, -1)) * y_pop, axis=1).reshape((-1, 1))
return x, y
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 2) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
def print_info(pop):
fitness,pred = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
return (x[max_fitness_index], y[max_fitness_index]),fitness[max_fitness_index],pred[max_fitness_index]
if __name__ == "__main__":
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2)) # matrix (POP_SIZE, DNA_SIZE)
point=[]
score=[]
accuracy=[]
for i in range(N_GENERATIONS): # 迭代N代
print('第{}代'.format(i))
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
# F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
fitness,_= get_fitness(pop)
pop = select(pop, fitness) # 选择生成新的种群
(x,y),output,acc=print_info(pop)
point.append((x,y))
score.append(output)
accuracy.append(acc)
for i in point:
print(i)
##绘制准确率随迭代次数的变换曲线
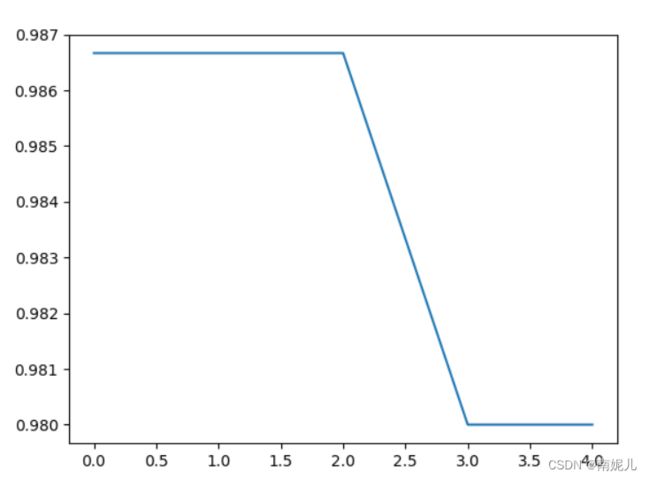
plt.plot(accuracy)
plt.show()上面的曲面是准确率随迭代次数的关系,可以看到在第一代和第二代的结果是比较好的。至于为什么迭代的越多,准确率下降的问题还需要研究。
参考文献:
遗传算法详解 附python代码实现_重学CS的博客-CSDN博客_python遗传算法
python遗传算法解简单整数规划与原理探究_m0_51810505的博客-CSDN博客_遗传算法整数规划
搭建简单的神经网络——使用pytorch实现鸢尾花的分类_yuekangwei的博客-CSDN博客_pytorch 鸢尾花