【pytorch】使用numpy实现pytorch的softmax函数与cross_entropy函数

1. torch.nn.functional.F.softmax

公式

$$Softmax(x_i)=\frac{\exp (x_i)}{{\sum }_j\exp (x_j)}$$

使用numpy实现

import numpy as np
import torch
import torch.nn.functional as F


def my_softmax(x):
    exp_x = np.exp(x)
    return exp_x/np.sum(exp_x)

x = np.array([1.5, 2.2, 3.1, 0.9, 1.2, 1.7])
xt = torch.from_numpy(x)


print('F.softmax:', F.softmax(xt))
print('my_softmax', my_softmax(x))

结果一致

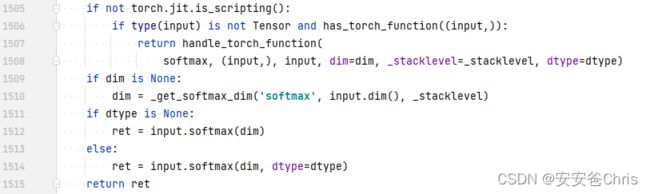
pytorch源码

从源码上来看，torch.nn.functional.F.softmax实际上调用的是Tensor自身的softmax函数

2. torch.nn.functional.F.log_softmax

公式

$$\begin{gathered} Log\_softmax(x_i)=ln\frac{\exp (x_i)}{{\sum }_j\exp (x_j)}(1) \\ =x_i-ln\sum _j\exp (x_j)(2) \end{gathered}$$

使用numpy实现

import numpy as np
import torch
import torch.nn.functional as F



def my_softmax(x):
    exp_x = np.exp(x)
    return exp_x/np.sum(exp_x)

def my_log_softmax1(x):
    return np.log(my_softmax(x))

def my_log_softmax2(x):
    return x-np.log(np.sum(np.exp(x)))

x = np.array([1.5, 2.2, 3.1, 0.9, 1.2, 1.7])
xt = torch.from_numpy(x)


print('F.softmax:', F.log_softmax(xt))
print('my_softmax', my_log_softmax1(x))
print('my_softmax', my_log_softmax2(x))

结果一致

---

3. torch.nn.functional.F.nll_loss

nll的全称是The negative log likelihood loss

公式

首先nll_loss并不是深度学习里独有的，它是个数学公式如下：
假设p和q两组概率集合
$$nll(p,q)=-\sum _{k}p(k)log(q(k))$$
换到我们的上下文中，Y是标签， P是观测概率集合，则有下面
$$nll(P，Y)=-\sum _{k}Y(k)log(P(k))$$
Y实际上是会转为one hot形式的向量，所以 对于y=k的情况下，Y(k) = 1;其他都是 Y(k) =0,则有如下，
$$nll(P，Y)=-\sum _{k}log(P(k))$$

所以这里要注意：

1. P和Y是有顺序的，不可以填反
2. Y是one hot编码的；但是实际上在使用时，只需要传入分类数组即可。在函数内，torch会把分类的组数做one-hot编码

pytorch源码

这里只贴关键部分：
从源码可见，nll_loss的计算实际上是调用c（torch）的代码。 这里发现其实输入Tensor维度不一定为2，如果4就是nll_loss2d。
这里是什么？有知道的小伙伴可以留言告知。

使用numpy实现

import numpy as np
import torch
import torch.nn.functional as F

def my_nll_loss(P, Y, reduction='mean'):
    loss = []
    for n in range(len(Y)):
        p_n = P[n][Y[n]]
        loss.append(p_n.item())

    if reduction == 'mean':
        return -np.mean(loss)

    if reduction == 'sum':
        return -np.sum(loss)

    return -np.mean(loss)

p = np.array([0.1, 0.4, 0.8, 0.2, 0.9, 0.2, 0.7, 0.1, 0.6]).reshape(3, 3)
y = np.array([1, 0, 2])
P = torch.from_numpy(p)
# class不需要做one_hot
# Y = F.one_hot(torch.from_numpy(y).long(), num_classes=3)
Y = torch.from_numpy(y).long()

print(my_nll_loss(p, y))
print(F.nll_loss(P, Y))

print(my_nll_loss(p, y, reduction='sum'))
print(F.nll_loss(P, Y, reduction='sum'))

结果一致

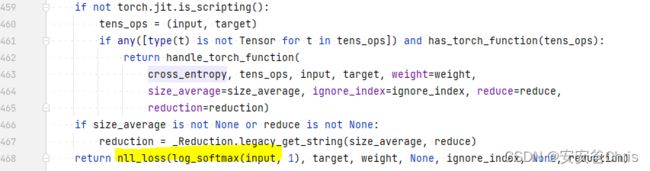
4. torch.nn.functional.F.cross_entropy

This criterion combines log_softmax and nll_loss in a single function

官网的公式如下：
$$\begin{gathered} \ell (x,y)=L=\{l_1,\dots ,l_N{\}}^{\top }, \\ {l}_n=-w_{y_n}\log \frac{\exp (x_{n,y_n})}{{\sum }_{c=1}^C\exp (x_{n,c})}\cdot 1\{y_n\ne \text{ignore\_index}\} \end{gathered}$$

这里有权重参数weights（其实这个权重是nll_loss中的），我们简单来看先省去这个weights。即
$$l_n=-\log \frac{\exp (x_{n,y_n})}{{\sum }_{c=1}^C\exp (x_{n,c})}\cdot 1\{y_n\ne \text{ignore\_index}\}$$

但是一般而言，这里的P(y)都会使用softmax来计算，所以有
$$cross\_entropy(P，Y)=-\sum _{k}log\_softmax(P(k)))$$

这就是cross_entropy, 即log_softmax and nll_loss

使用numpy实现

import numpy as np
import torch
import torch.nn.functional as F


def my_softmax(x):
    output = np.zeros(x.shape)
    for n in range(x.shape[0]):
        exp_x = np.exp(x[n, :])
        output[n] = (exp_x / np.sum(exp_x))

    return output


def my_log_softmax(x):
    return np.log(my_softmax(x))

def my_nll_loss(P, Y, reduction='mean'):
    loss = []
    for n in range(len(Y)):
        p_n = P[n][Y[n]]
        loss.append(p_n.item())

    if reduction == 'mean':
        return -np.mean(loss)

    if reduction == 'sum':
        return -np.sum(loss)

    return -np.mean(loss)


p = np.array([0.1, 0.4, 0.8, 0.2, 0.9, 0.2, 0.7, 0.1, 0.6]).reshape(3, 3)
y = np.array([1, 0, 2])
P = torch.from_numpy(p)
# Y = F.one_hot(torch.from_numpy(y).long(), num_classes=3)
Y = torch.from_numpy(y).long()

print('my_nll_loss:', my_nll_loss(my_log_softmax(p), y))
print('F.cross_entropy:', F.cross_entropy(P, Y))

print('my_nll_loss:', my_nll_loss(my_log_softmax(p), y, reduction='sum'))
print('F.cross_entropy:', F.cross_entropy(P, Y, reduction='sum'))

结构一致

pytorch源码

其实现逻辑如注释所示，

5. torch.nn.functional.F.binary_cross_entropy

另外提一下BCE， 即binary_cross_entropy。

有的初学者可能会误以为是两个class分类的cross_entropy。其实这是一个很大的误解。

它实际上是P集合中每一个概率是true/false中一种的概率，跟cross_entropy不同的是，P中每一个子维度是每个class的分布概率。

公式

$$\begin{gathered} \ell (x,y)=L=\{l_1,\dots ,l_N{\}}^{\top }, \\ {l}_n=-w_n\left[y_n\cdot \log x_n+(1-y_n)\cdot \log (1-x_n)\right] \end{gathered}$$
首先，Y不再是分类index数组，而它是一组概率，即表示是某一种（两种中某一种分类）的概率；所以在输入时，如果按照F.cross_entropy的index数组输入的话，会有如下错误。

ValueError: Using a target size (torch.Size([3])) that is different to the input size (torch.Size([3, 2])) is deprecated. Please ensure they have the same size

其次，它的Y输入是同P的维度

使用numpy实现

import numpy as np
import torch
import torch.nn.functional as F

def my_bce(P, Y, reduction='mean'):
    loss = []
    for i in range(P.shape[0]):
        l = Y[i] * np.log(P[i]) + (1 - Y[i]) * np.log((1 - P[i]))
        loss.append(l)

    if reduction == 'mean':
        return -np.mean(loss)

    if reduction == 'sum':
        return -np.sum(loss)

    return -np.mean(loss)


p = np.array([0.1, 0.9, 0.8, 0.2, 0.9, 0.1, 0.3, 0.4, 0.5]).reshape(3, 3)
y = np.array([1, 0, 1, 0, 0, 1, 1, 1, 1]).reshape(3, 3)
P = torch.from_numpy(p)
Y = torch.from_numpy(y).double()

print('my_bce:', my_bce(p, y))
print('F.binary_cross_entropy:', F.binary_cross_entropy(P, Y))

结果一致

---

参考文档

1. https://zhuanlan.zhihu.com/p/145341251
2. https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss
3. https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/