DFS搜索和输出所有路径
文章目录
- 1、DFS搜所有路径
- 2、用栈记录和输出路径
- 3、例题
-
- 3.1 C++代码
- 3.2 Python代码
- 4、真题
-
- 4.1 C++代码
- 4.2 Python代码
2022.12将出版蓝桥杯大赛用书《蓝桥杯大赛-程序设计竞赛专题挑战教程》,作者:蓝桥杯组委会、罗勇军。
这本书解析了蓝桥杯大赛的常见考点,所有例题用C/C++、Python两种语言给出代码,适合C/C++组和Python组入门。
本文的内容摘抄自这本书。
1、DFS搜所有路径
DFS是一种暴力搜索,它能搜所有可能的情况。
蓝桥杯大赛常常涉及到路径问题,需要用DFS寻找路径和输出路径,一般是输出一条符合要求的路径。
DFS的特点是“一路到底”,遇到终点时,就得到了从起点到终点的一条路径。所以搜所有路径用DFS写代码最方便。下面看DFS如何找到所有的路径。
图中,'@‘表示起点,’*‘表示终点,’.‘是可以走的点,’#'是墙壁不能走。
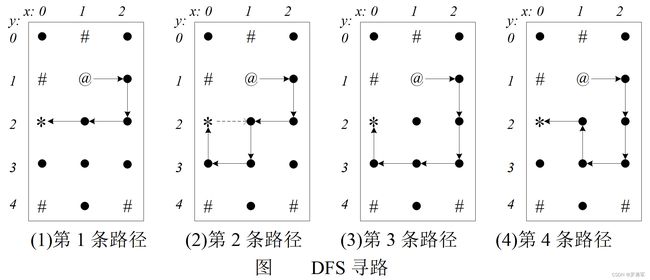
图(1)是搜到的第一条路径。从起点(1, 1)出发,查询它的“左-上-右-下”哪个方向能走,发现“左-上”不能走,可以走“右”。第一步走到右边的(2,1)。然后从(2, 1)继续走,它可以向上走到(2, 0),但是后面就走不通了,退回来改走下面的(2, 2)。按这个方法,逐步深入走到终点,最后得到一条从起点(1, 1)到终点(0, 2)的路径“(1,1)->(2,1)->(2,2)->(1,2)->(0,2)”。后面C++代码中的a[nx][ny] = '#'的作用是“保存现场”。在这次DFS深入过程中,这条路径上曾经路过的点被“保存现场”,不允许再次经过。到达终点后,从终点退回,回溯寻找下一个路径。代码中的a[nx][ny] = '.'的作用是退回后“恢复现场”。
图(2)是搜到的第二条路径。在图(1)搜到一条路径后,从终点(0, 2)退回到(1, 2),继续向下走到(1, 3)、(0, 3)、(0, 2)。
图(3)是搜到的第三条路径。从终点(0, 2)一路退回到(2, 2)后,才找到新路径。在退回的过程中,原来被“保存现场的”(0, 3)、(1, 3)、(0, 2),重新被“恢复现场”,允许被经过。例如(1, 3),在第二条路径中曾用过,这次再搜新路径时,在第三条路径中重新经过了它。如果不“恢复现场”,这个点就不能在新路径中重新用了。
总结“保存现场”和“恢复现场”的作用:
(1)“保存现场”的作用,是禁止重复使用。当搜索一条从起点到终点的路径时,这条路径上经过的点,不能重复经过,否则就兜圈子了,所以路径上的点需要“保存现场”,禁止再经过它。没有经过的点,或者碰壁后退回的点,都不能“保存现场”,这些点可能后面会进入这条路径。
(2)“恢复现场”的作用。当重新搜新的路径时,方法是从终点(或碰壁的点)沿着旧路径逐步退回,每退回一个点,就对这个点“恢复现场”,允许新路径重新经过这个点。例如图(2)和图(3)的点(1, 3)。
2、用栈记录和输出路径
在DFS中,用栈来跟踪DFS的过程,记录走过的路径,是最方便的。DFS到某个格子时,把这个格子放到栈里,表示路径增加了这个格子。DFS回溯的时候,退出了这个格子,表示路径上不再包括这个格子,需要从栈中弹走这个格子。
3、例题
下面是本文自创的例题,演示上述的两个功能:
(1)用DFS搜索从起点到终点的所有路径;
(2)用栈记录路径。
例题:输出所有路径
【题目描述】给出一张格子图,输出从起点到终点的所有路径。
【输入描述】第一行是整数n,m,分别是行数和列数。后面n行,每行m个符号。只有两种符号:’•’能走,’#’是墙壁不能走。在每一步,都按左-上-右-下的顺序搜索。左上角是起点,坐标(0, 0),右下角是终点,坐标(n-1, m-1)。
【输出描述】输出所有的路径。为了方便表示,约定每个小格子用一个数字代表,从西北角(左上角)开始编号: 0, 1, 2, 3…
【样例输入1】
3 2
..
..
..
【样例输出1】
0 2 4 5
0 2 3 5
0 1 3 2 4 5
0 1 3 5
【样例输入2】
3 4
....
..#.
....
【样例输出2】
0 4 8 9 5 1 2 3 7 11
0 4 8 9 10 11
0 4 5 1 2 3 7 11
0 4 5 9 10 11
0 1 5 4 8 9 10 11
0 1 5 9 10 11
0 1 2 3 7 11
3.1 C++代码
下面代码中的函数dfs()搜索出所有代码,并打印出来。
vector
#include3.2 Python代码
下面的Python代码和上面的C++代码逻辑一样。注意它使用栈的方法,用一个list数组 path=[]模拟栈。
def dfs(x,y):
if x==n-1 and y==m-1: #到达终点
for i in range(len(path)): print(path[i],end=' ')
print() #换行
return
dir = ((-1, 0), (0, -1),(1, 0), (0, 1)) #4个方向:左、上、右、下
for u,v in dir: #遍历4个方向的邻居
nx = x+u; ny = y+v #邻居的坐标
if 0<=nx<n and 0<=ny<m and a[nx][ny]=='.':
a[nx][ny]='#' #保存现场:这个点在这次更深的dfs中不能再用
path.append(nx*m + ny) #进栈,把这个点记录到路径里
dfs(nx, ny)
path.pop(); #出栈,释放这个点
a[nx][ny]='.' #恢复现场:回溯后这个点可以再次用
n,m = map(int, input().split()) #n行、m列
a=[]
for i in range(n): #读图,存到二维矩阵a[n][m],n行m列
a.append(list(input()))
path = [] #用栈记录路径
path.append(0)
a[0][0]='#'
dfs(0,0)
4、真题
下面的真题,是上面讲解的知识点的直接应用。
路径之谜 2016年第七届决赛,lanqiaoOJ第89题 https://www.lanqiao.cn/problems/89/learning/
【题目描述】小明冒充X星球的骑士,进入了一个奇怪的城堡。城堡里边什么都没有,只有方形石头铺成的地面。假设城堡地面是n×n个方格。按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有n个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
【输入格式】第一行一个整数N(0
又是一道格子搜索题,这种题在蓝桥杯大赛中很常见。
题目要求输出一条路径,用DFS是很合适的,DFS搜索过程中,自然生成一条路径。
每走到一个格子,对应的靶子上箭多一支,靶子上的箭等于给定的数字后,就不用再DFS下去了。这是一个简单的剪枝。
注意DFS时记录路径的技巧。根据题目的要求,用栈来跟踪DFS的过程,记录DFS走过的路径,是最方便的。DFS到某个格子时,把这个格子放到栈里,表示路径增加了这个格子。DFS回溯的时候,退出了这个格子,表示路径上不再包括这个格子,需要从栈中弹走这个格子。
4.1 C++代码
#include4.2 Python代码
def dfs(x,y):
if a[x]<0 or b[y]<0: return
if x==n-1 and y==n-1:
ok=1
for i in range(n):
if a[i]!=0 or b[i]!=0: ok=0; break
if ok==1:
for i in range(len(path)): print(path[i],end=' ')
for d in [(1,0),(-1,0),(0,1),(0,-1)]:
tx = x+d[0]; ty = y+d[1]
if 0 <= tx < n and 0 <= ty < n and vis[tx][ty] == 0:
vis[tx][ty] = 1
path.append(tx*n + ty) #进栈,记录路径
a[tx] -= 1; b[ty] -= 1
dfs(tx, ty)
path.pop(); #出栈,DFS回溯
a[tx] += 1; b[ty] += 1
vis[tx][ty] = 0
n = int(input())
vis = [[0]*n for i in range(n)]
path = [] #用栈记录路径
path.append(0)
b = list(map(int,input().split()))
a = list(map(int,input().split()))
vis[0][0]=1
a[0] -= 1; b[0] -= 1
dfs(0,0)