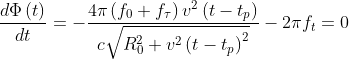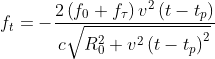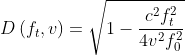SAR学习笔记-SAR成像算法系列（一）

SAR系列文章目录

最近想把自己对SAR了解的有关内容整理成一个系列：

《SAR学习笔记》简单介绍了SAR技术发展历程，并以尽量简洁的语言描述了SAR的基本原理，并与其他雷达技术做了简单对比，介绍了SAR的巧妙之处；

《SAR学习笔记-代码部分》承接《SAR学习笔记》介绍了雷达领域一些常见场景的仿真，对于初学或者学习一段时间雷达的学者，这部分简单易上手；

《SAR学习笔记后续-phased工具箱介绍》针对对传统相控阵雷达场景，利用MATLAB自带工具箱进行构建，这部只是对phased工具结合简单的仿真场景做了介绍，只是对想要深入研究雷达的学者起到抛砖引玉的作用；

       上述文章可以作为SAR系列文章的前言导读部分，接下来将分别介绍SAR成像核心公式推导、后向投影算法（BPA）、距离多普勒算法（RDA）、线性调频变标算法（CSA）、距离徙动算法（wKA）、极坐标格式算法（PFA）、星载模式下的机载等效、干涉SAR、极化SAR等。这些内容将会是我最近一段时间更新的主线内容，当然也会根据情况更新一些其他内容：傅里叶变换、分数傅里叶变换等信号处理工具。

---

目录

SAR系列文章目录

前言

一、信号建模

二、信号模型的四域表示

2.1.距离时域-方位时域

2.2.距离频域-方位时域

2.3.距离频域-方位频域（二维频域）

2.4.距离时域-方位频域（距离多普勒域）

总结

---

前言

       SAR成像算法本质是对二维信号的脉冲压缩：距离维靠设计大时宽带宽积脉冲信号实现快时间维脉冲压缩；方位维靠多普勒信号展宽实现慢时间维脉冲压缩。

       脉冲压缩理论只是对SAR成像原理轮廓的简单直观勾勒，对于初学者，想要进一步熟悉SAR成像算法甚至实现SAR成像，一个关键内容就是对SAR成像场景中信号模型的理解。

       SAR成像场景中的信号模型是各类SAR成像算法的基础，也是各类成像算法针对实现信号模型中某些操作（如脉冲压缩）过程中所遇到问题所用方法的基础。为此，需要单独介绍SAR成像中的信号模型。

---

一、信号建模

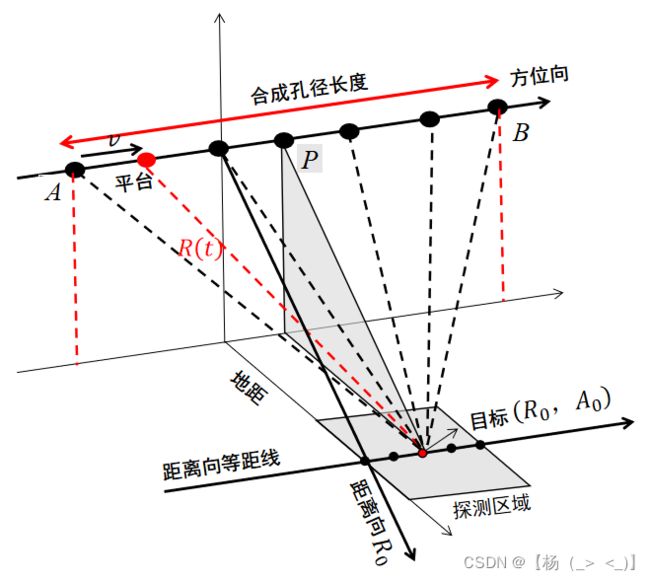
       SAR成像是对一个区域的散射特性进行成像，这个区域的地形一般比较复杂，区域内不同位置处的物体散射特性各不相同，最后SAR接收的是探测区域内所有物体后向散射信号的叠加，整个探测区域散射的回波信号模型非常复杂。直接构造整个探测区域的散射信号模型十分困难，也没有必要。为了简化信号模型，信号模型的建立运用了两个离散化：探测区域的离散化；平台飞行的离散化。

       探测区域离散化：将探测区域认为是若干散射点的集合，由此对区域回波信号模型的建立转化为对这些散射点回波信号模型的建立。这样只需构建任意散射点的回波信号模型即可表示整个探测区域的回波信号模型。该离散化的准则是：离散间隔内的物体散射特性基本不变。

      平台飞行离散化：将平台的飞行过程认为是一个“走停”模式，即在一个脉冲时间（脉冲重复周期）内，平台是“停”（静止）的状态，平台发射一个脉冲信号，并在该位置处接收该脉冲照射目标的回波信号；在下一个脉冲时间内，平台“走”（瞬移）到另一个位置（按照原来匀速运动应该走到的位置处），并在下一个位置重复上一个脉冲时间内平台的操作。该离散化的准则是：电磁波传播速度远大于平台速度，即SAR一次发射、接收过程中，雷达的位置基本不变。（星载SAR，由于星地距离远，雷达发射接收信号的时间间隔超过了一个脉冲时间宽度，但通过合理设计脉冲重复周期，还是能适用的）

      上图为SAR探测场景图，针对红点目标，SAR波束正视照射，从A点开始照射目标，到P点离目标最近，并在B点刚好离开红点目标。平台从A到B都能接收到红点目标的回波信号，假设平台时刻飞行到红点位置，雷达发射脉冲信号，此时接收的回波信号为：

       其中表示处目标的散射面积，表示合成孔径时长。理想情况可以认为是矩形窗，实际上是由实孔径天线的方向图构成，考虑信号往返，函数为天线方向图的平方。  

      考虑平台每次停留发射的信号相干（每次发射的信号相位一致），不失一般性，参数可以认为是变量，即针对红点目标，任意时刻（慢时间时刻）的回波信号为：

         

其中距离。

       从图示不难发现，与红点目标相比，距离向等距的黑点目标多普勒历程一致，只是对应的方位向时延不一样，反映在表达式上，即距离目标最短的时刻不同。对接收的回波信号进一步化简可得：

其中：

       将SAR（信号发射到接收的过程）看成一个系统，则为对应的系统函数，该系统函数包含了目标位置处的散射面积，由此，SAR成像问题等效为：根据发射信号从回波信号中反卷积出系统函数。所以SAR成像最终所成的像是物体雷达散射面积的像。

       从统函数中可以看出，重建函数的快时间维存在慢时间维的耦合项，为此SAR成像算法一个关键的步骤是去除这个耦合项，称为距离徙动校正，通过距离徙动校正，将SAR系统函数校正成，此时快时间维与慢时间维相互独立，可以分别对快时间维和慢时间信号做脉冲压缩处理，得到SAR图像。

       上述是SAR回波信号模型的建立过程以及对所得回波信号模型的简单分析，在建立信号模型的过程中，运用了雷达领域经常用到了两个概念，这里简单说明一下，不做细节的讲解。简单理解，慢时间是对脉冲间时间的标记，即慢时间表示发射的是第几个脉冲信号，所以慢时间本身是离散的，离散间隔为脉冲重复周期；快时间是对脉冲内时间的标记，即快时间显示的是任意一个脉冲内的时刻，相比慢时间，快时间是连续的，需要通过信号的采样来离散。

二、信号模型的四域表示

       上节主要推导了SAR回波信号的时域模型，在实际SAR成像处理中，为了处理效率的提升，诸如脉冲压缩、距离徙动校正以及相位补偿等不只是在时域进行，下面简单介绍SAR信号的四域表达式。为了进行实质性的信号模型的四域表达，发射信号以chirp信号为例，表达式为

其中为发射信号的调频率，为信号时宽，为发射载波频率。

2.1.距离时域-方位时域

       将式（2）代入（1）得回波信号：

      回波信号下变频得：

      式（3）即为SAR成像处理用到的信号模型距离时域-方位时域表达式。从表达式可以看出，慢时间维的多普勒信号主要由载波信号产生。

2.2.距离频域-方位时域

        对信号的快时间维进行傅里叶变换，得：

       基于驻定相位原理POSP（在相位变化缓慢的地方积分有值，在相位变化剧烈的地方积分正负相抵，积分为零，所以最终积分的结果为驻定相位处的函数值），相位表达式为：

令

则：

由此：

化简得：

      式（4）即为SAR成像处理用到的信号模型距离频域-方位时域表达式。从表达式可以看出，多普勒信号是载频和快时间频率共同作用的结果，即快时间维的chirp信号也对方位维多普信号产生做出了贡献。

2.3.距离频域-方位频域（二维频域）

         对信号的慢时间维进行傅里叶变换，得：

       基于POSP，相位表达式为：

令

则：

其中

由此：

其中

      式（5）即为SAR成像处理用到的信号模型距离频域-方位频域表达式。从表达式可以看出，显示了距离徙动现象。

2.4.距离时域-方位频域（距离多普勒域）

         理论上可以直接对信号的慢时间维进行傅里叶变换得其距离多普勒域表达式，但是由于距离与方位之间的相位耦合，直接利用POSP求解困难，因此可以对信号的慢时间维进行逆傅里叶变换，得：

       基于POSP，相位表达式为：

为了求导的简便，将上述相位进行二阶泰勒展开得：

其中

令

则

其中

其中

由此：

其中

      式（6）即为SAR成像处理用到的信号模型距离时域-方位频域表达式。从表达式可以看出，多普勒现象也会作用于距离维，导致距离维chirp信号的调频发生变化，虽然变化很小，但是对最终成像影响很大。

       本节主要分析SAR正视下的回波信号建模，斜视情况类似，只是方位向（慢时间维）的时延为波束中心时刻。

---

总结

        本章核心公式为（3）（4）（5）（6），这四个公式为后面SAR成像算法的基础。这四个公式本质上都是SAR的回波信号（基带信号），只是从不同变换域来描述。以chirp类型的发射信号为例，四个域变换的计算主要用到POSP原理，为推导距离多普勒表达式时对积分相位做了近似处理，该近似处理使得信号的适用范围为小斜视角的成像场景。