ICLR2022系列解读之四：更有效的图像压缩概率模型Entroformer

本文解读我们ICLR2022上发表的论文《Entroformer: A Transformer-based Entropy Model for Learned Image Compression》。这篇文章针对图像压缩中的全局信息冗余，提出一种基于Transformer的概率模型：Entroformer。它使用Transformer中的Attention机制来实现全局相关性和局部相关性的联合学习。针对图像压缩任务，该方法提出了一种Top-k过滤机制和一种新的相对位置模块，使得该概率模型能够更有效地预测特征的概率分布。同时，该方法又将单向的串行上下文模型扩展到双向的并行上下文模型，来加速解码过程。该方法不仅得到了更优的压缩效果，同时保证了解压过程的高效性。

论文地址：http://arxiv.org/abs/2202.05492

开源代码：https://github.com/mx54039q/entroformer

一、前言

图像压缩是计算机视觉领域较为基础性的一个课题。随着近些年深度学习的发展，基于深度学习的图像压缩算法逐渐超越了传统方法，具有较大的研究价值。卷积神经网络（CNN）能够学习到更好的压缩特征表达，而且基于深度学习的概率模型也能够更好地估计压缩特征的概率。虽然基于CNN的方法有较强的局部相关性建模能力，但是建模全局相关性的能力较弱。图1展示了图像中的全局信息冗余。因此，在图像压缩中建模全局相关性能够进一步提升压缩性能。

图1 图像中的全局信息冗余

为了更好地提取图像中的全局冗余性，我们将Transformer的结构融合到图像压缩任务中来。Transformer的网络结构天然契合图像压缩任务，能够较好地学习特征的相关性。基于Transformer的基础结构，我们提出了针对图像压缩任务的改进点，来提升图像压缩的性能。

二、背景

图像压缩的目标是在保证关键信息的不丢失的前提下，减小储存或传输的码率。主流的图像压缩标准，比如JPEG、JPEG2000、HEVC/H.265、VVC，通过精细设计的手工特征和复杂的处理得到了较好的性能。随着近些年深度学习的发展，基于深度学习的图像压缩算法逐渐超越了传统方法，具有较大的研究价值。目前比较主流的深度学习图像压缩模型主要包含三个部分，编码网络（Encoder）、概率模型（Entropy Model）、解码网络（Decoder）。如图2所示，基于学习的方法先将输入图片经过Encoder得到压缩特征 y ，将进行量化到得到 y^1。 概率模型(Entropy Model)的作用是估计出压缩特征的熵概率模型，从而可以对压缩特征进行编解码。这里的熵概率模型一般以高斯分布作为先验，然后用模型去估计高斯分布的均值和方差，压缩特征基于该高斯分布得到的概率表用作编解码。概率模型估计得越准确，则消耗的码率越小。经过编解码后的 y^ 输入到Decoder中得到恢复的解压缩图像。现有的深度学习方法基本都是使用卷积神经网络，主要对局部相邻特征进行学习。但是在图像压缩任务中，还有一部分的全局冗余性没有被挖掘，这部分重复的特征会造成码率的重复消耗。

图2 基于深度学习的图像压缩算法框架

三、方法

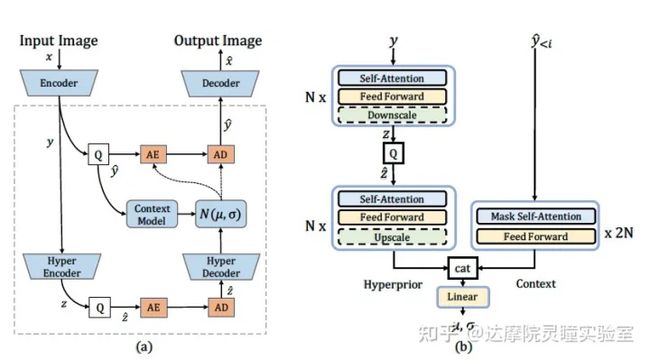
本文提出的方法旨在学习一个性能更好的概率模型，通过对图像中的全局冗余性进行建模，从而进一步提升压缩性能。整体结构图如图3，

图3 (a) 基于学习的图像压缩模型的网络结构. 虚线框内展示了概率模型, 由context model和hyperprior model组成. (b) 概率模型的具体网络结构.

主体的Encoder和Decoder我们沿用了之前的方法 encoder和decoder都是4层卷积。概率模型我们使用了纯Transformer的结构，结合了上下文预测模块（Context Model）和超先验概率模块（Hyperprior）。对于模型整体的优化目标，是在更少的压缩特征的码率消耗下提升输出图像的重建质量。这里，码率消耗是指压缩特征基于概率模型给出的最小平均码长，由估计的高斯分布和压缩特征的边缘分布之间的香农交叉熵给出。图像的重建质量一般为Mean Square Error (MSE) 或者MS-SSIM两种图像相似度的评价指标。整体的损失函数如下

L=R+λD=Ex∼px[−log2⁡py^(y^)]⏟rate (latents)+Ex∼px[−log2⁡pz^(z^)]⏟rate (hyper-latents)+λ⋅Ex∼px||x−x^||22⏟distortion,

Transformer中使用Self-attention模块来进行特征的学习，形式如下：

Attention(X)=softmax(XWQ(XWK)Tdk)XWV

其中， X 为模块的输入特征，WQ,WK,WV 分别为Query, Key, Value的参数矩阵。

3.1 针对图像压缩的相对位置编码

为了探究位置信息在图像压缩任务中的影响，我们设计了一个验证性实验。我们去除了Transformer中的位置信息模块，在训练中对Self-attention加入了随机mask，然后测试每个相对位置对于压缩性能的影响。结果如图4所示：

图4 特征的相对位置对于压缩性能的影响

可以看到，位置对于图像压缩性能的影响呈现出与L1距离正相关的情形，并且在相对距离大于一定值后对于压缩性能的影响较小。基于这个实验现象，我们构建了L1边界约束的相对位置编码：

eij=xiWQ(xjWK+pijK)Tdk

pijK=wclip(ai−j,h)Kclip(ai−j,h)={ai−j‖ai−j‖1<=h(h,h)otherwise.

pijK 为可学习的相对位置编码， ai−j 为二维相对坐标， h 为L1边界的值。当L1距离大于 h ，我们使用同一个位置编码。

3.2 Top-k机制

引入Transformer之后，虽然对全局相关性能够更好地建模，但也引入了很多不相关的噪声。为了过滤这部分噪声，我们改进了Self-attention，只选择相似度最高的k个特征，

V′=softmax(fk(Q(K+P)Tdk))V

fk(eij)={eijif eij is within the top-k largest elements in row j−∞otherwise.

该操作提升了模型的性能，并且提升了模型的训练稳定性。

3.3 并行双向Context Model加速

由于原始的单向Context Model是存在因果关系的，所以在解压时需要串行操作，该方法在GPU上的速度较慢。我们借鉴了CVPR21的方法（Checkerboard Context Model），在压缩效果和速度性能上进行平衡。基于Transformer的并行双向Context Model能更有效地学习双向context信息，使得我们的模型比Checkerboard Context Model有更好的平衡性能。并行双向的Context Model如下图所示，

图5 压缩特征被分为两部分。第一部分只用hyperprior进行参数的估计。然后第二部分特征用第一部分特征作为context，结合hyperprior进行参数的估计。由于预测第二部分参数时所有context都已可见，所以可以并行计算。

四、实验结果

我们主要在Kodak数据集上进行了各个模块的对比实验。

(1) 位置编码

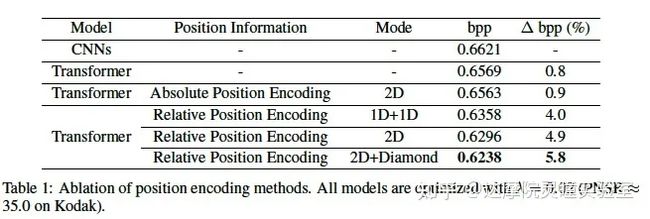
我们分别比较了不同的位置编码方法，其中CNN方法以及没有位置编码的Transformer方法作为对照组。可以看到在图像压缩任务上，相对位置编码的效果优于绝对位置编码。本文提出的Diamond RPE还有0.9%压缩率的提升。

(2) Top-k过滤机制

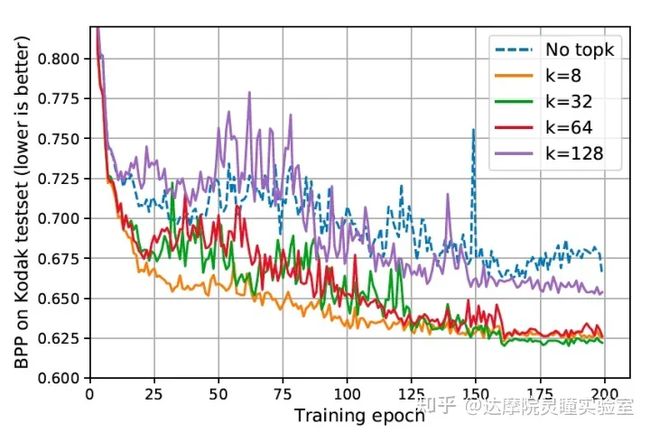
图6 Tok-k过滤机制的收敛曲线。

我们对比了不同k值下模型的训练bpp曲线来验证Top-k过滤机制的影响，并且以去除top-k作为对照组。可以看到，引入Top-k过滤机制后，Entroformer模型不仅提升了稳定性，对最终的压缩性能也有较高的提升。

(3) 并行双向Context Model

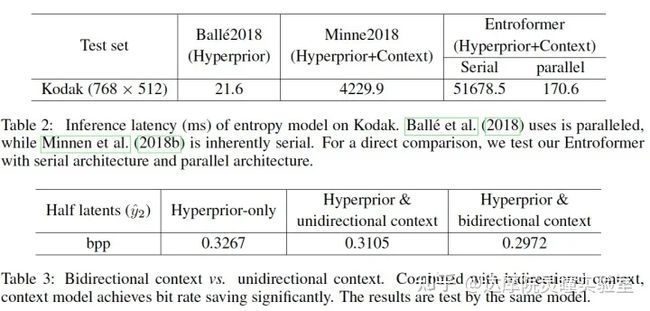
我们在表2中对比了不同模型的解码速度（GPU下）。可以看到，并行双向Context Model比串行单向context model方法更快。另外，我们在表3中比较了双向Context和单向context的压缩效果。相对于单向context，双向context可以利用更丰富的上下文信息，所以能够获得更好的压缩效果。

(4) Comparison of State-of-the-Arts

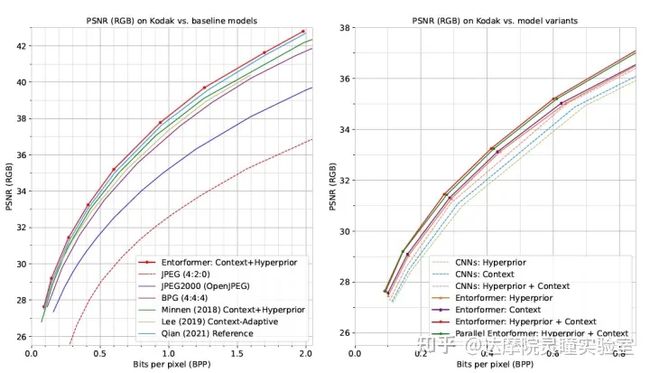
​图7 左图为本方法与SOTA方法的Rate-Distortion (RD)曲线对比；右图为CNN方法与Entroformer方法在不同的entropy model设置下的RD曲线对比。

我们在Kodak数据集上验证了本文方法Entroformer的性能。图6左图展示了与SOTA方法的Rate-Distortion (RD)曲线对比，我们的方法比CNN方法有5.2%的码率节省，比BPG（H264的帧内压缩方法）有20.5%的码率节省。图6右图展示了CNN方法与Entroformer方法在不同的entropy model设置下的RD曲线对比。可以看到我们的Entroformer方法相对于CNN方法有较大的优势。另外，我们还对比了并行双向Context Model和串行单向context model方法的效果，并行双向Context Model在大幅加速的前提下，效果略微下降（不到1%）。

(5) 可视化

图8 Attention map的可视化。

图9 Tok-k过滤机制的可视化。