【模型代码】STFGNN(未完)
STFGNN(spatial-temporal fusion graph neural networks)
文章解读:《csdn-STFGNN阅读笔记》
克服的问题:
它们通常利用独立的模块来实现空间和时间相关性,或者它们只使用独立的组件来捕获局部或全局的异构依赖关系
细节捕捉:
通过对不同时间周期的不同时空图进行并行处理,SFTGNN可以有效地学习隐藏的时空相关性。
一、模型def construct_model(config)
- 参数以及为数据的模型参数
def construct_model(config):
from models.stsgcn_4n_res import stsgcn # 导入stsgcn
module_type = config['module_type'] # 模型类型:'individual'
act_type = config['act_type'] # 激活函数:'GLU'
temporal_emb = config['temporal_emb'] # 时间嵌入:'true'
spatial_emb = config['spatial_emb'] # 空间嵌入:'true'
use_mask = config['use_mask'] # 使用mask:'true'
batch_size = config['batch_size'] # :32
num_of_vertices = config['num_of_vertices'] # 顶点个数:358
num_of_features = config['num_of_features'] # 特征个数:1
points_per_hour = config['points_per_hour'] # 每小时的时间点个数:12
num_for_predict = config['num_for_predict'] # 预测个数:12
adj_filename = config['adj_filename'] # 邻接矩阵csv文件名
id_filename = config['id_filename'] # 数据txt文件名
二、生成邻接矩阵get_adjacency_matrix
- 参数及案例对应值
def get_adjacency_matrix(distance_df_filename, num_of_vertices,
type_='connectivity', id_filename=None):
'''
Parameters
----------
distance_df_filename: str, path of the csv file contains edges information 文件路径
num_of_vertices: int, the number of vertices 顶点个数 358
type_: str, {connectivity, distance} 矩阵的含义:连接性,距离
Returns
----------
A: np.ndarray, adjacency matrix
提示:文件中的节点的index是从0开始的,因为numpy的索引是从0开始的,要一致啊
'''
- 代码解析
用numpy创建(顶点个数*顶点个数)的全0矩阵,用于存储邻接矩阵
import csv
A = np.zeros((int(num_of_vertices), int(num_of_vertices)),
dtype=np.float32)
如果是txt文件读取
A = np.zeros((int(num_of_vertices), int(num_of_vertices)),
dtype=np.float32)
# 读取csv文件,两个节点之间,如果有距离,则其邻接矩阵对应元素为1,无向的
if id_filename:
with open(id_filename, 'r') as f:
id_dict = {int(i): idx
for idx, i in enumerate(f.read().strip().split('\n'))} # 字符串.strip()默认删除开头结尾的空白符
with open(distance_df_filename, 'r') as f:
f.readline() # readline() 是python的内置函数,每次读取一行,返回一个字符串对象 # 这行应该没用
reader = csv.reader(f) # csv.reader 是将每行的数据当作列表(list)返回,读取全部行的数据
for row in reader:
if len(row) != 3: # 确定每行有三个元素,否则用continue跳过该行
continue
i, j, distance = int(row[0]), int(row[1]), float(row[2]) # 字符改为数字
A[id_dict[i], id_dict[j]] = 1
A[id_dict[j], id_dict[i]] = 1
return A
读取csv的距离文件,分两类:connectivity and distance
# Fills cells in the matrix with distances.
with open(distance_df_filename, 'r') as f:
f.readline()
reader = csv.reader(f)
for row in reader:
if len(row) != 3:
continue
i, j, distance = int(row[0]), int(row[1]), float(row[2])
if type_ == 'connectivity':
A[i, j] = 1
A[j, i] = 1
elif type == 'distance':
A[i, j] = 1 / distance
A[j, i] = 1 / distance0
else:
raise ValueError("type_ error, must be "
"connectivity or distance!")
return A
三、生成两个大矩阵
3.1 生成空间4N的矩阵def construct_adj(A, steps)
def construct_adj(A, steps):
'''
construct a bigger adjacency matrix using the given matrix
Parameters
----------
A: np.ndarray, adjacency matrix, shape is (N, N)
steps: how many times of the does the new adj mx bigger than A
Returns
----------
new adjacency matrix: csr_matrix, shape is (N * steps, N * steps)
'''
N = len(A)
adj = np.zeros([N * steps] * 2) # 生成4N* 4N 的矩阵
# 主对角线上的矩阵 为 A
for i in range(steps):
adj[i * N: (i + 1) * N, i * N: (i + 1) * N] = A
# 次对角线上的矩阵 为E
for i in range(N):
for k in range(steps - 1):
adj[k * N + i, (k + 1) * N + i] = 1
adj[(k + 1) * N + i, k * N + i] = 1
# 设置大矩阵的主对角线的元素 为1
for i in range(len(adj)):
adj[i, i] = 1
return adj
3.2 生成融合的4N矩阵``def construct_adj_fusion`
def construct_adj_fusion(A, A_dtw, steps):
'''
construct a bigger adjacency matrix using the given matrix
Parameters
----------
A: np.ndarray, adjacency matrix, shape is (N, N)
steps: how many times of the does the new adj mx bigger than A
Returns
----------
new adjacency matrix: csr_matrix, shape is (N * steps, N * steps)
----------
This is 4N_1 mode:
[T, 1, 1, T
1, S, 1, 1
1, 1, S, 1
T, 1, 1, T]
'''
N = len(A)
adj = np.zeros([N * steps] * 2) # "steps" = 4 !!! # 4N*4N 的全零矩阵
# 设置主对角线上的元素
for i in range(steps):
if (i == 1) or (i == 2):
adj[i * N: (i + 1) * N, i * N: (i + 1) * N] = A # 对角线上两个 S
else:
adj[i * N: (i + 1) * N, i * N: (i + 1) * N] = A_dtw # 对角线上两个 T
# 设置次对角线上的元素 ,应为单位矩阵
for i in range(N):
for k in range(steps - 1):
# 下面两行索引相反,为对称
adj[k * N + i, (k + 1) * N + i] = 1 # 大矩阵【0,1】,大矩阵【1,2】,大矩阵【2,3】
adj[(k + 1) * N + i, k * N + i] = 1
# 设置反对角线上的两个 T
adj[3 * N: 4 * N, 0: N] = A_dtw #adj[0 * N : 1 * N, 1 * N : 2 * N] 应该注释错了
adj[0 : N, 3 * N: 4 * N] = A_dtw #adj[0 * N : 1 * N, 1 * N : 2 * N]
# 设置third对角线上的4个 E
adj[2 * N: 3 * N, 0 : N] = adj[0 * N : 1 * N, 1 * N : 2 * N]
adj[0 : N, 2 * N: 3 * N] = adj[0 * N : 1 * N, 1 * N : 2 * N]
adj[1 * N: 2 * N, 3 * N: 4 * N] = adj[0 * N : 1 * N, 1 * N : 2 * N]
adj[3 * N: 4 * N, 1 * N: 2 * N] = adj[0 * N : 1 * N, 1 * N : 2 * N]
# 将大矩阵的主对角线设为1
for i in range(len(adj)):
adj[i, i] = 1
return adj
四、数据模型搭建
4.1 生成序列def generate_seq
def generate_seq(data, train_length, pred_length):
seq = np.concatenate([np.expand_dims(
data[i: i + train_length + pred_length], 0)
for i in range(data.shape[0] - train_length - pred_length + 1)],
axis=0)[:, :, :, 0: 1]
return np.split(seq, 2, axis=1)
- 看列表推导式中的循环范围:
data.shape[0] (样本个数)-train_length(训练长度)-pred_length(预测长度)+1=test+val的总样本的最大索引+1(range取左不取右)
- 看列表推导式中的循环元素:
data[i:i+train_length+pred_length] 切片的长度为train_length+pred_lenght
- 升维、合并示意图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hE9GDkUG-1619751230295)(C:\Users\hp\Pictures\文截图\生成序列示意图.png)]

- 查看切片范围
【:,:,:,0:1】可以看到前三维的索引都全取,而最后一维的索引只取index=0
对于4维数组,在模型中,我们一般会改变后两维的数组。将后两维构成的表格单独拿出来看,也就是表格中的列
- 数据的均分
np.split(seq, 2, axis=1 ) # 显然在 axis=1 均匀割裂,会返回一个列表,列表中有2个元素
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jrXmol77-1619751230298)(C:\Users\hp\Pictures\文截图\split_axis=1.png)]
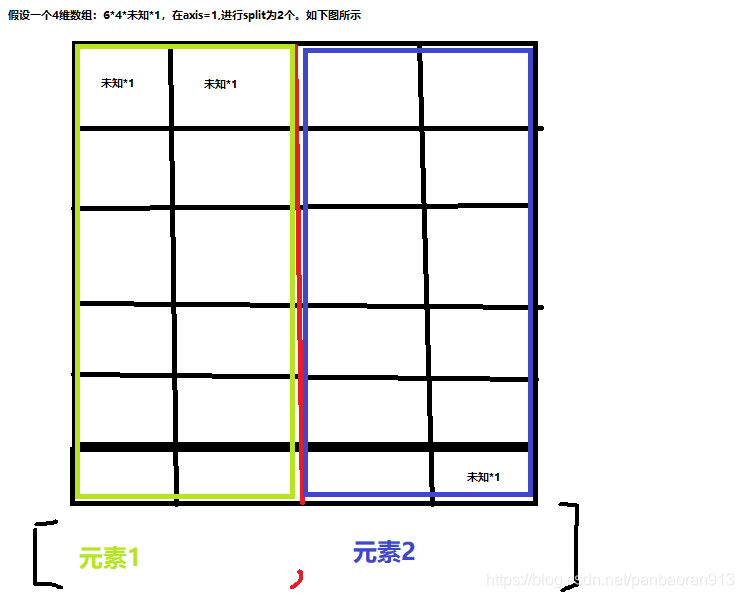
会通过两种关键字来生成数据,一种是train_val_test,另一种是data
4.2 通过关键字train-val-test生成数据
def generate_from_train_val_test(data, transformer):
mean = None
std = None
for key in ('train', 'val', 'test'):
x, y = generate_seq(data[key], 12, 12)
if transformer:
x = transformer(x)
y = transformer(y)
if mean is None:
mean = x.mean()
if std is None:
std = x.std()
yield (x - mean) / std, y
-
如果 transformer 不是none(即一个转换函数,没找到),则对特征x,标签y进行转换
-
之后,求特征x的均值和标准差,对x进行标准化
-
yield是函数返回迭代器,返回3个次,分别为train,val,test
4.3 通过关键字data生成数据
def generate_from_data(data, length, transformer):
mean = None
std = None
train_line, val_line = int(length * 0.7), int(length * 0.8) # 训练分界线,验证分界线,下可以看到三个集合不重叠
for line1, line2 in ((0, train_line),
(train_line, val_line),
(val_line, length)):
x, y = generate_seq(data['data'][line1: line2], 12, 12)
if transformer:
x = transformer(x)
y = transformer(y)
if mean is None:
mean = x.mean()
if std is None:
std = x.std()
yield (x - mean) / std, y
- 划分训练集、验证集、测试集,三个集合不重叠
- 判断是否对特征x,标签y进行转换
- 求特征x的均值和标准差,对x进行标准化
- yield是函数返回迭代器,返回3个次,分别为train,val,test
4.4 两种生成数据的方式打包
def generate_data(graph_signal_matrix_filename, transformer=None):
'''
shape is (num_of_samples, 12, num_of_vertices, 1)
'''
data = np.load(graph_signal_matrix_filename) # 加载图信号矩阵文件
keys = data.keys() # 获取关键字列表,下面判断两种生成数据的方式
if 'train' in keys and 'val' in keys and 'test' in keys:
for i in generate_from_train_val_test(data, transformer):
yield i
elif 'data' in keys:
length = data['data'].shape[0]
for i in generate_from_data(data, length, transformer):
yield i
else:
raise KeyError("neither data nor train, val, test is in the data")
五、生成train-val-test数据
- 拼接路径,读取数据,选取数据
- 对数据集分别用均值对0值进行替换,数据再归一化
def generate_data_train_val_test(dataset_dir_h5, data_dir, transformer=None):
'''
shape is (num_of_samples, 12, num_of_vertices, 1)
achieve data from train/val/test.npz separately.
pd.read_hdf('文件名',key='关键字’) 读入hdf5格式的压缩文件,是pandas库默认支持的
'''
df = pd.read_hdf(dataset_dir_h5) # 文件路径字符串为"data/pems-bay.h5"
df_mean = df[df != 0].mean() # (207, )
df_std = df[df !=0].std() # (207, )
# 下:加载拼接路径获取数据,然后数据选取
data_train = np.load(os.path.join(data_dir, 'train.npz')) # data_dir:"data/PEMS-BAY/" 路径拼接
train_x, train_y = data_train['x'][:,:,:,0], data_train['y'][:,:,:,0] # metr-la: (23974, 12, 207), (23974, 12, 207)
data_val = np.load(os.path.join(data_dir, 'val.npz'))
val_x, val_y = data_val['x'][:,:,:,0], data_val['y'][:,:,:,0] # metr-la: (3425, 12, 207), (3425, 12, 207)
data_test = np.load(os.path.join(data_dir, 'test.npz'))
test_x, test_y = data_test['x'][:,:,:,0], data_test['y'][:,:,:,0]# metr-la: (6850, 12, 207), (6850, 12, 207)
for road_ix in range(df.shape[1]):
road_mean = df_mean.tolist()[road_ix]
road_std = df_std.tolist()[road_ix]
# Padding zero value of Training set to mean value, Train_x normalization... 用均值去填充0值,训练x 归一化
train_x_block = train_x[:,:,road_ix] #(23974, 12)
train_x_block_pad = pd.DataFrame(train_x_block)
train_x_block_pad.replace(0, road_mean, inplace=True)
train_x_block_pad = (np.array(train_x_block_pad) - road_mean) / road_std
train_x[:,:,road_ix] = train_x_block_pad
train_y_block = train_y[:,:,road_ix] #(23974, 12)
train_y_block_pad = pd.DataFrame(train_y_block)
train_y_block_pad.replace(0, road_mean, inplace=True)
train_y[:,:,road_ix] = train_y_block_pad
# Padding zero value of Validation set to mean value, valid_x normalization...
val_x_block = val_x[:,:,road_ix] #(3425, 12)
val_x_block_pad = pd.DataFrame(val_x_block)
val_x_block_pad.replace(0, road_mean, inplace=True)
val_x_block_pad = (np.array(val_x_block_pad) - road_mean) / road_std
val_x[:,:,road_ix] = val_x_block_pad
val_y_block = val_y[:,:,road_ix] #(3425, 12)
val_y_block_pad = pd.DataFrame(val_y_block)
val_y_block_pad.replace(0, road_mean, inplace=True)
val_y[:,:,road_ix] = val_y_block_pad
# Padding zero value of Test set(test_x) to mean value, test_x normalization...
test_x_block = test_x[:,:,road_ix] #(6850, 12)
test_x_block_pad = pd.DataFrame(test_x_block)
test_x_block_pad.replace(0, road_mean, inplace=True)
test_x_block_pad = (np.array(test_x_block_pad) - road_mean) / road_std
test_x[:,:,road_ix] = test_x_block_pad
# Test y keep "0" for fair comparison with previous baselines
# test_y keep the same....
return train_x[:,:,:,np.newaxis], train_y, val_x[:,:,:,np.newaxis], val_y, test_x[:,:,:,np.newaxis], test_y