ASTGCN(二)函数解析
ASTGCN(二)函数解析
数据来源:
数据来自于https://github.com/Davidham3/ASTGCN,PEMS04和08都在其中有下载。
整体框架:
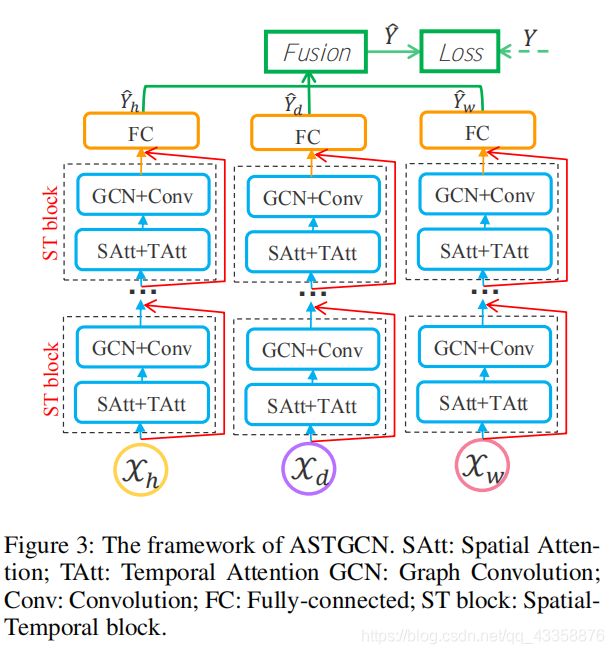
原文中作者的思路是通过xh,xd和xw分别经过三个步骤最后卷积求和。所以在文章的实现上,作者首先分别设计SAtt和TAtt(这里我觉得就是叫空间注意力和时间注意力),然后经过图卷积和卷积核函数(本文中是ReLU),最后经过全链接之后Final fusion得到最终预测流量数据,再计算损失函数。
(PS:有不对的地方望纠正^^)
SAtt(空间注意力)与TAtt(时间注意力):
也就是原文中Spatial-Temporal Attention这一部分,原文中以Th(recent)为例介绍空间注意力权值的计算:
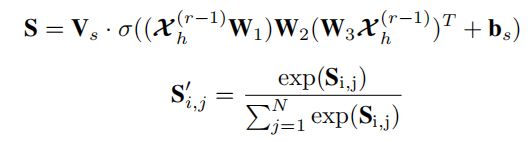
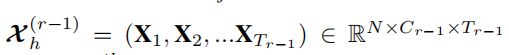
这一部分我认为主要需要理解的是这几个量的维数的定义。
涉及的主要是N,Cr-1和Tr-1。
N:文章中解释的是节点个数,通俗一点就是传感器数量。
Cr-1:第r-1层的特征维数,第0层卷积就是三个维度(occupy,flow,speed)
Tr-1:第r-1层时间片的长度,第0层对应三个时间片(hour,day,week)分别就是Th,Td和Tw。
然后几个学习参数明确:Vs,W1,W2,W3,bs。这几个都是学习的参数。
class Spatial_Attention_layer(nn.Block): #空间注意力机制层
#使用Block无需定义求导或反传函数,MXNet会使用autograd对forward自动生成相应的backward函数
def __init__(self, **kwargs):
super(Spatial_Attention_layer, self).__init__(**kwargs)
with self.name_scope():
self.W_1 = self.params.get('W_1', allow_deferred_init=True)
self.W_2 = self.params.get('W_2', allow_deferred_init=True)
self.W_3 = self.params.get('W_3', allow_deferred_init=True)
self.b_s = self.params.get('b_s', allow_deferred_init=True)
self.V_s = self.params.get('V_s', allow_deferred_init=True)
def forward(self, x):
'''
Parameters
----------
x: mx.ndarray, x^{(r - 1)}_h,
shape is (batch_size, N, C_{r-1}, T_{r-1})
Returns
----------
S_normalized: mx.ndarray, S', spatial attention scores
shape is (batch_size, N, N)
'''
# get shape of input matrix x
_, num_of_vertices, num_of_features, num_of_timesteps = x.shape
# defer the shape of params
self.W_1.shape = (num_of_timesteps, )
self.W_2.shape = (num_of_features, num_of_timesteps)
self.W_3.shape = (num_of_features, )
self.b_s.shape = (1, num_of_vertices, num_of_vertices)
self.V_s.shape = (num_of_vertices, num_of_vertices)
for param in [self.W_1, self.W_2, self.W_3, self.b_s, self.V_s]:
param._finish_deferred_init()
# compute spatial attention scores
# shape of lhs is (batch_size, V, T)
lhs = nd.dot(nd.dot(x, self.W_1.data()), self.W_2.data()) #x^{(r - 1)}_h*W1*W2
# shape of rhs is (batch_size, T, V)
rhs = nd.dot(self.W_3.data(), x.transpose((2, 0, 3, 1))) #x^{(r - 1)}_h*W3
# shape of product is (batch_size, V, V)
product = nd.batch_dot(lhs, rhs)
S = nd.dot(self.V_s.data(),
nd.sigmoid(product + self.b_s.data())
.transpose((1, 2, 0))).transpose((2, 0, 1))
# normalization
S = S - nd.max(S, axis=1, keepdims=True)
exp = nd.exp(S)
S_normalized = exp / nd.sum(exp, axis=1, keepdims=True)
return S_normalized
我们看到前面的几个都很好理解,在归一化的时候文章也提到用了一个softmax function,就是代码中 S = S - nd.max(S, axis=1, keepdims=True)来保证权值问题。
时间注意力和空间注意力类似,不再赘述。
引入图卷积:
在这里文章考虑到计算量的问题用了一个切比雪夫多项式来近似拉普拉斯矩阵特征值分解,也就是我们看到的下列这个表达式:
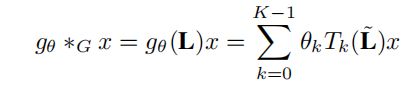
其中涉及四个参数的问题:
首先最简单的K:切比雪夫多项式的次数,这个在setting这一块给出实验使用的K的值为3。configurations里面可以看到K=3。
θ:切比雪夫多项式向量系数参数,看完后我觉得还是训练的参数(有不对望纠正)
Tk:这个就是切比雪夫多项式,递归公式定义为:
![]()
其中:
![]()
最后就是L~:
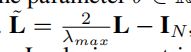
其中λmax是拉普拉斯矩阵的最大特征值,也就是L矩阵分解的最大特征值,L=D-A,其中D是度矩阵,A是邻接矩阵。项目中有一个distance的csv文件保存了传感器节点之间的距离,文章认为存在这一条距离信息则认为两点相互连接。IN就是一个单位矩阵。
引入注意力权值本文中是通过卷积实现。
![]()
堆叠时间维度标准卷积层,将x换成引入时间注意力之后的,个人觉得就是单纯的卷积运算堆叠。代码中实现是通过下述堆叠实现的:
spatial_At = self.SAt(x_TAt)
综合的公式如下:
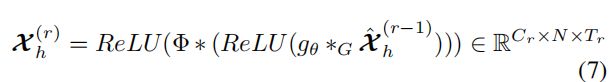
实现部分代码如下:
(一)切比雪夫多项式定义
#定义切比雪夫多项式中的L~
def scaled_Laplacian(W):
assert W.shape[0] == W.shape[1]
D = np.diag(np.sum(W, axis=1))
L = D - W
lambda_max = eigs(L, k=1, which='LR')[0].real
return (2 * L) / lambda_max - np.identity(W.shape[0])
#切比雪夫多项式递归
def cheb_polynomial(L_tilde, K):
N = L_tilde.shape[0]
cheb_polynomials = [np.identity(N), L_tilde.copy()]
for i in range(2, K):
cheb_polynomials.append(
2 * L_tilde * cheb_polynomials[i - 1] - cheb_polynomials[i - 2]) #L_tilde即公式中的x
return cheb_polynomials
(二)空间注意力权值
class Spatial_Attention_layer(nn.Block): #空间注意力机制层
#使用Block无需定义求导或反传函数,MXNet会使用autograd对forward自动生成相应的backward函数
'''
compute spatial attention scores
'''
def __init__(self, **kwargs):
super(Spatial_Attention_layer, self).__init__(**kwargs)
with self.name_scope():
self.W_1 = self.params.get('W_1', allow_deferred_init=True)
self.W_2 = self.params.get('W_2', allow_deferred_init=True)
self.W_3 = self.params.get('W_3', allow_deferred_init=True)
self.b_s = self.params.get('b_s', allow_deferred_init=True)
self.V_s = self.params.get('V_s', allow_deferred_init=True)
def forward(self, x):
# get shape of input matrix x
_, num_of_vertices, num_of_features, num_of_timesteps = x.shape
# defer the shape of params
self.W_1.shape = (num_of_timesteps, )
self.W_2.shape = (num_of_features, num_of_timesteps)
self.W_3.shape = (num_of_features, )
self.b_s.shape = (1, num_of_vertices, num_of_vertices)
self.V_s.shape = (num_of_vertices, num_of_vertices)
for param in [self.W_1, self.W_2, self.W_3, self.b_s, self.V_s]:
param._finish_deferred_init()
# compute spatial attention scores
# shape of lhs is (batch_size, V, T)
lhs = nd.dot(nd.dot(x, self.W_1.data()), self.W_2.data()) #x^{(r - 1)}_h*W1*W2
# shape of rhs is (batch_size, T, V)
rhs = nd.dot(self.W_3.data(), x.transpose((2, 0, 3, 1))) #x^{(r - 1)}_h*W3
# shape of product is (batch_size, V, V)
product = nd.batch_dot(lhs, rhs)
S = nd.dot(self.V_s.data(),
nd.sigmoid(product + self.b_s.data())
.transpose((1, 2, 0))).transpose((2, 0, 1))
# normalization
S = S - nd.max(S, axis=1, keepdims=True)
exp = nd.exp(S)
S_normalized = exp / nd.sum(exp, axis=1, keepdims=True)
return S_normalized
(三)图卷积结合
class ASTGCN_block(nn.Block):
def __init__(self, backbone, **kwargs):
super(ASTGCN_block, self).__init__(**kwargs)
K = backbone['K']
num_of_chev_filters = backbone['num_of_chev_filters']
num_of_time_filters = backbone['num_of_time_filters']
time_conv_strides = backbone['time_conv_strides']
cheb_polynomials = backbone["cheb_polynomials"]
with self.name_scope():
self.SAt = Spatial_Attention_layer()
self.cheb_conv_SAt = cheb_conv_with_SAt(
num_of_filters=num_of_chev_filters,
K=K,
cheb_polynomials=cheb_polynomials)
self.TAt = Temporal_Attention_layer()
self.time_conv = nn.Conv2D(
channels=num_of_time_filters, #64
kernel_size=(1, 3), #卷积核1*3
padding=(0, 1), #右边补0(?)
strides=(1, time_conv_strides))
self.residual_conv = nn.Conv2D(
channels=num_of_time_filters,
kernel_size=(1, 1),
strides=(1, time_conv_strides))
self.ln = nn.LayerNorm(axis=2)
def forward(self, x):
(batch_size, num_of_vertices,
num_of_features, num_of_timesteps) = x.shape
# shape is (batch_size, T, T)
temporal_At = self.TAt(x)
x_TAt = nd.batch_dot(x.reshape(batch_size, -1, num_of_timesteps),
temporal_At)\
.reshape(batch_size, num_of_vertices,
num_of_features, num_of_timesteps)
# cheb gcn with spatial attention
spatial_At = self.SAt(x_TAt)
spatial_gcn = self.cheb_conv_SAt(x, spatial_At)
# convolution along time axis
time_conv_output = (self.time_conv(spatial_gcn.transpose((0, 2, 1, 3)))
.transpose((0, 2, 1, 3)))
# residual shortcut
x_residual = (self.residual_conv(x.transpose((0, 2, 1, 3)))
.transpose((0, 2, 1, 3)))
return self.ln(nd.relu(x_residual + time_conv_output))