Python实现Feature selection for multi-label classification using multivariate mutual information文章算法

本博客实验代码源自如下文章所提算法思想：

 LEE J，KIM D W． Feature Selection for Multi-label Classification
Using Multivariate Mutual Information． Pattern Recognition Letters，
2013，34(3): 349 －357．

该算法的核心是下面这个公式：

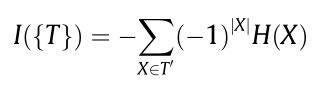
就是通过这个公式可以计算出三元变量的互信息。再通过对高维联合熵进行近似计算，结合前向贪心搜索，过滤出特征子集。
由于有大量的重复计算，算法的计算量极其巨大，所以我在复现代码的时候，把一些需要重复计算的保存下来，后面再计算的时候直接调用，但后面计算的过程中仍然有大量重复计算的步骤，这里就没有继续优化了。
该文章给出了源代码，源代码地址：（需要）

http://ml.cau.ac.kr/?f=softwares&m=pmu

另外，这也是他们实验室的地址，他们实验室所发表的文章代码及数据集都在那个地址里，需要的自己去找。

源代码是MATLAB语言，本人机器上无法运行，所以用Python重写了一遍，经过测试，结果是可以对的上的。（性能可能不如MATLAB下优秀，没有用矩阵计算）
代码如下，需要的自取，转载请注明原创，如有错误，请及时告知本人，谢谢！

"""
    Author: wzk
    Date:   2020-10-28
    theme:  多元变量互信息多标签特征选择
"""
from settings.setting import *
from sklearn.preprocessing import KBinsDiscretizer
import numpy as np
import math
import scipy.io as si


class PMU:

    def __init__(self, train_data, train_target, info):
        """
        初始化类的成员
        """
        self.train_data = train_data
        self.train_target = train_target
        self.info = info
        self.k_num = 30
        pass

    def dis_efi(self, data):
        """
        对数据离散化，暂时是2折离散，返回结果的数据集中元素为1或者2
        :return:
        """
        segmentation = 2
        after_sort_data = np.sort(data, axis=0)
        dis_seg = np.linspace(0, data.shape[0]-1, segmentation + 1)
        dis_data = np.zeros([segmentation, data.shape[1]])
        for i in range(data.shape[1]):
            for j in range(segmentation):
                dis_data[j, i] = after_sort_data[int(dis_seg[j + 1] + 0.5), i]
        # todo:未做去重，因为暂时用到的几个数据集没有需要去重的。源代码中有去重这一行
        res = np.ones([data.shape[0], data.shape[1]])
        for i in range(data.shape[1]):
            for j in range(data.shape[0]):
                for k in range(segmentation):
                    if data[j, i] > dis_data[k, i]:
                        res[j, i] += 1

        return res
        pass

    def p_entropy(self, data):
        """
        计算数据的信息熵
        :return:
        """
        # res_data = self.dis_efi(data)
        # 按行统计数据中重复的次数
        a = list([tuple(i) for i in data])
        b = dict((i, a.count(i)) for i in a)
        c = list(b.values())

        ent = 0
        for i in c:
            ent += -(i/data.shape[0])*(math.log(i/data.shape[0], 2))

        return ent
        pass

    def get_ent(self):
        """
        如果是第一次运行一个数据集，先执行这里，计算出该数据集的基本信息，存入mat文件中
        后面执行时，不需要再花费大量时间重复计算，减少程序运行时间
        :return:
        """
        dis_train_data = self.dis_efi(self.train_data)
        # 记录每个特征自己的信息熵
        ent_f = list()
        for i in range(self.train_data.shape[1]):
            ent_f.append(self.p_entropy(dis_train_data[:, i].reshape(-1, 1)))
        # 记录每个标签自己的信息熵
        ent_l = list()
        for i in range(self.train_target.shape[1]):
            ent_l.append(self.p_entropy(self.train_target[:, i].reshape(-1, 1)))
        # 记录特征与标签间的信息熵
        ent_f_with_l_array = np.zeros([self.train_data.shape[1], self.train_target.shape[1]])
        for i in range(self.train_data.shape[1]):
            for j in range(self.train_target.shape[1]):
                join_data = np.insert(dis_train_data[:, i].reshape(-1, 1), 1, self.train_target[:, j], axis=1)
                ent_f_with_l_array[i, j] += self.p_entropy(join_data)
        # 记录标签与标签间的信息熵
        ent_l_with_l_array = np.zeros([self.train_target.shape[1], self.train_target.shape[1]])
        for i in range(self.train_target.shape[1]):
            for j in range(i, self.train_target.shape[1]):
                join_target = np.insert(self.train_target[:, i].reshape(-1, 1), 1, self.train_target[:, j], axis=1)
                ent_l_with_l_array[i, j] += self.p_entropy(join_target)

        # 记录新添加特征与标签间的信息熵
        ent_f_with_l_list = list()
        for i in range(self.train_data.shape[1]):
            ent = 0
            for j in range(self.train_target.shape[1]):
                ent += ent_f[i] + ent_l[j] - ent_f_with_l_array[i, j]
            ent_f_with_l_list.append(ent)

        # 记录新添加特征与整体标签间的三元信息熵
        ent_f_with_l_and_l_list = list()
        for i in range(self.train_data.shape[1]):
            ent = 0
            for j in range(self.train_target.shape[1]):
                for k in range(j, self.train_target.shape[1]):
                    join_target = np.insert(self.train_target[:, j].reshape(-1, 1), 1, self.train_target[:, k],
                                            axis=1)
                    join_target = np.insert(join_target, 2, dis_train_data[:, i], axis=1)
                    ent_f_l_l = self.p_entropy(join_target)
                    ent += ent_f[i] + ent_l[j] + ent_l[k] - ent_f_with_l_array[i, j] - ent_f_with_l_array[
                        i, k] - \
                           ent_l_with_l_array[j, k] + ent_f_l_l
            ent_f_with_l_and_l_list.append(ent)

        file_path = 'excels/' + self.info.get('basic_settings').get('data') + '/' + self.info.get('basic_settings').get(
            'data') + '_ent.mat'
        si.savemat(file_path, {
            'ent_f': ent_f,
            'ent_l': ent_l,
            'ent_f_with_l_list': ent_f_with_l_list,
            'ent_f_with_l_and_l_list': ent_f_with_l_and_l_list,
            'ent_f_with_l_array': ent_f_with_l_array,
            'ent_l_with_l_array': ent_l_with_l_array,
            'dis_train_data': dis_train_data
        })
        pass

    def pmu(self):
        """
        过滤式特征选择
        :return:
        """
        try:
            file_path = 'excels/' + self.info.get('basic_settings').get('data') + '/' + self.info.get(
                'basic_settings').get('data') + '_ent.mat'
            ent_f = si.loadmat(file_path).get('ent_f')[0]
            ent_l = si.loadmat(file_path).get('ent_l')[0]
            ent_f_with_l_list = si.loadmat(file_path).get('ent_f_with_l_list')[0]
            ent_f_with_l_and_l_list = si.loadmat(file_path).get('ent_f_with_l_and_l_list')[0]
            ent_f_with_l_array = si.loadmat(file_path).get('ent_f_with_l_array')
            ent_l_with_l_array = si.loadmat(file_path).get('ent_l_with_l_array')
            dis_train_data = si.loadmat(file_path).get('dis_train_data')
        except Exception as e:
            print("先执行get_ent方法！")
            exit()

        evaluate_list = [ent_f_with_l_and_l_list[i] - ent_f_with_l_list[i] for i in range(self.train_data.shape[1])]
        index_list = list()
        index_list.append(np.argsort(np.array(evaluate_list))[0])

        # 找到第一个特征之后，在剩下的特征中依次循环
        for p in range(self.k_num - 1):
            # 计算新添加特征与原有特征子集以及标签集间的信息熵大小
            ent_f_with_f_and_l_list = list()
            for i in range(self.train_data.shape[1]):
                if i in index_list:
                    # 不能缺失，缺失之后，无法准确定位特征索引；所以加入负无穷，不管怎么样都不会影响
                    ent_f_with_f_and_l_list.append(float('-inf'))
                    continue
                print("正在选取第%d" % (p + 2) + "轮特征,当前循环第%d" % i + "个特征")
                ent = 0
                for j in range(len(index_list)):
                    for k in range(self.train_target.shape[1]):
                        join_data = np.insert(dis_train_data[:, i].reshape(-1, 1), 1, dis_train_data[:, index_list[j]],
                                              axis=1)
                        ent_join_data = self.p_entropy(join_data)
                        join_data_with_data_with_target = np.insert(join_data, 1, self.train_data[:, k], axis=1)
                        ent_j = self.p_entropy(join_data_with_data_with_target)
                        ent += ent_f[i] + ent_f[index_list[j]] + ent_l[k] - ent_f_with_l_array[i, k] - \
                               ent_f_with_l_array[index_list[j], k] - ent_join_data + ent_j
                ent_f_with_f_and_l_list.append(ent)

            # 计算新添加特征与原有标签间的信息熵大小
            f_evaluate_list = [evaluate_list[i] - ent_f_with_f_and_l_list[i] for i in range(self.train_data.shape[1])]
            index_list.append(np.argsort(np.array(f_evaluate_list))[0])

        return index_list
        pass