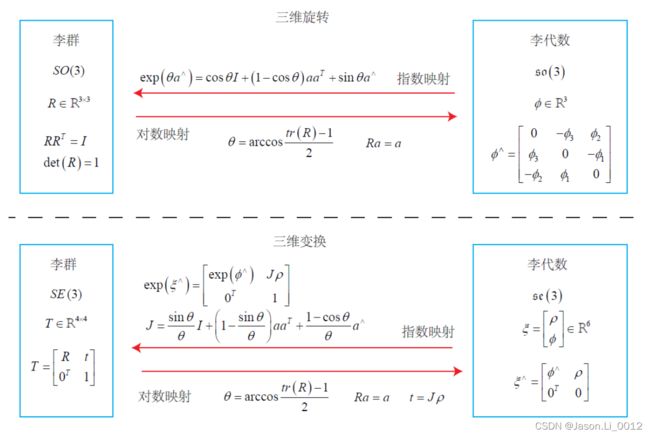
李群李代数：SO(3)和SE(3)

群论

定义

群（Group）是一种集合加上一个二元运算。

设$G$是一个非空集合，$\cdot$是一个二元运算，若满足如下条件：

• 封闭性： $\forall a,b\in G,a\cdot b\in G$
• 结合律： $\forall a,b,c\in G,(a\cdot b)\cdot c=a\cdot (b\cdot c)$
• 单位元（幺元）： $\exists e\in G,s.t.\forall a\in Ga\cdot e=e\cdot a=a$
• 逆元： $\forall a\in G,\exists a^{-1}\in G,s.t.a\cdot a^{-1}=a^{-1}\cdot a=e$

则称$G$对$\cdot$构成一个群，记作$(G,\cdot )$。

• 称$G$上二元运算$\cdot$为“乘法”
• $a\cdot b$为$a$与$b$的积，简写$ab$
• 若群$G$中元素有限，则称其为有限群，反之则称其为无限群
• 有限群的元素个数称为有限群的阶

子群

对于群$(G,\cdot )$存在$H\subset G$且$H\ne \varnothing$，若$(H,\cdot )$也是一个群，则称$H$为$G$的子群。子群的充要条件如下：
$$HH=H且H^{-1}=H$$

李群

李群是一种具有连续（光滑）性质的群，它既是群也是流形。

刚体能够连续地在空间中运动，故而特殊正交群$SO(n)$和特殊欧式群$SE(n)$为李群。

李代数

定义

每个李群都有与之对应的李代数，李代数描述了李群单位元附近的正切空间性质。

李代数由一个集合$V$，一个数域$F$以及一个二元运算$[,]$组成，记为$(V,F,[,])$。其中二元运算$[,]$被称为李括号，表示了两元素间的差异。

李代数满足如下条件：

• 封闭性： $\forall X,Y\in V,[X,Y]\in V$

• 双线性： $\forall X,Y,Z\in V,a,b\in F$有：
  $$\begin{gathered} [aX+bY,Z]=a[X,Z]+b[Y,Z] \\ [Z,aX+bY]=a[Z,X]+b[Z,Y] \end{gathered}$$

• 自反性： $\forall X\in V,[X,X]=0$

• 雅可比等价： $\forall X,Y,Z\in V,[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0$

• 反对称性： $\forall X,Y\in V,[X,Y]=-[Y,X]$

推导（SO(3)李代数）

对于任意旋转矩阵$R$，满足$R{R}^T=I$。刚体在三维空间中的运动是连续的，随时间而变换，也即：
$$R(t)R(t{)}^T=I$$
两侧对时间$t$进行求导：
$$\begin{array}{rl}\dot{R}(t)R(t{)}^T& +R(t)\dot{R}(t{)}^T=0\\ \dot{R}(t)R(t{)}^T& =-R(t)\dot{R}(t{)}^T\\ \dot{R}(t)R(t{)}^T& =-(\dot{R}(t)R(t{)}^T{)}^T\end{array}$$
由此，可知$\dot{R}(t)R(t{)}^T$为反对称矩阵，记$\dot{R}(t)R(t{)}^T=\varphi (t{)}^{\wedge }$，等式两侧右乘$R(t)$：
$$\begin{array}{rl}\dot{R}(t)& =\varphi (t{)}^{\wedge }R(t)\\ \dot{R}(t)& =\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ {\varphi }_3& 0& -{\varphi }_1\\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]R(t)\end{array}$$
由上式可知，每对旋转矩阵求一次导数，只需对其左乘一个$\varphi (t{)}^{\wedge }$。

$SO(3)$的单位元为：$t_0=0,R(0)=I$，将$R(t)$在单位元附近进行一阶泰勒展开：
$$\begin{array}{rl}R(t)& \approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ & =I+\varphi (t_0{)}^{\wedge }R(t_0)(t-t_0)\\ & =I+\varphi (t_0{)}^{\wedge }t\end{array}$$
$\varphi$反应了旋转矩阵$R$的导数性质，称其在$SO(3)$原点附近的正切空间上。

设$t_0$附近$\varphi$为常数不变：$\varphi (t_0)={\varphi }_0$，则有：
$$\dot{R}(t)={\varphi }_0^{\wedge }R(t)$$
在初始条件$R(0)=I$下解微分方程，得到：
$$R(t)=exp({\varphi }_0^{\wedge }t)$$
上式称为李代数$so(3)$的指数映射关系。

李代数so(3)

向量空间：$so(3)=\{\Phi ={\varphi }^{\wedge }\in {\Re }^{3\times 3}|\varphi \in {\Re }^3\}$

数域：$\Re$

李括号：$[{\varphi }_a,{\varphi }_b]={\Phi }_a{\Phi }_b-{\Phi }_b{\Phi }_a$
$$\begin{array}{rl}[{\varphi }_a,{\varphi }_b]& ={\Phi }_a{\Phi }_b-{\Phi }_b{\Phi }_a\\ & ={\varphi }_a^{\wedge }{\varphi }_b^{\wedge }-{\varphi }_b^{\wedge }{\varphi }_a^{\wedge }\\ & =({\varphi }_a^{\wedge }{\varphi }_b{)}^{\wedge }\in so(3)\end{array}$$
其中$\Phi ={\varphi }^{\wedge }$，为反对称矩阵：
$$\Phi =\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ {\varphi }_3& 0& -{\varphi }_1\\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]\in {\Re }^{3\times 3}$$

视集合${\Re }^3$和叉乘运算作为$se(3)$

李代数se(3)

向量空间：$se(3)=\{\Xi ={\xi }^{\wedge }\in {\Re }^{4\times 4}|\xi \in {\Re }^6\}$

数域：$\Re$

李括号$[{\Xi }_1,{\Xi }_2]={\Xi }_1{\Xi }_2-{\Xi }_2{\Xi }_1$
$$\begin{array}{rl}[{\Xi }_a,{\Xi }_b]& ={\Xi }_a{\Xi }_b-{\Xi }_a{\Xi }_b\\ & ={\xi }_a^{\wedge }{\xi }_b^{\wedge }-{\xi }_b^{\wedge }{\xi }_a^{\wedge }\\ & =({\xi }_1^{\star }{\xi }_2{)}^{\wedge }\in se(3)\end{array}$$
其中，参量$\xi$用于表示平移加旋转：
$$\xi =\left[\begin{array}{c}\rho \\ \varphi \end{array}\right],\rho \in {\Re }^3,\varphi \in so(3)$$
${\xi }^{\wedge }$非反对称矩阵，但仍保留记法：
$${\xi }^{\wedge }=\left[\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ 0^T& 0\end{array}\right]\in {\Re }^{4\times 4}$$

星计算${\xi }^{\star }$定义为：
$${\xi }^{\star }={\left[\begin{array}{c}\rho \\ \varphi \end{array}\right]}^{\star }=\left[\begin{array}{cc}{\varphi }^{\wedge }& {\rho }^{\wedge }\\ 0& {\varphi }^{\wedge }\end{array}\right]\in {\Re }^{6\times 6}$$
视集合${\Re }^6$和星计算为$se(3)$

指数映射与对数映射

指数映射反应了从李代数到李群的转换，任意矩阵的指数映射可写成一个泰勒展开，其结果仍是一个矩阵：
$$exp(G)=\sum _{n=0}^{\infty }\frac{1}{n!}{G}^n$$
对数映射则反应了从李群到李代数的转换：
$$\ln (G)=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{n+1}(G-I{)}^{n+1}$$

李群$SO(3)$李代数$so(3)$

$\varphi$是一个向量，定义其模长为$\theta$方向为$a$，$\varphi =\theta a$。其中，$a$为一个模长为1的单位向量：$\Vert \begin{array}{c}a\end{array}\Vert =1$。

对于反对称矩阵$a^{\wedge }$，易得：
$$\begin{array}{rl}式1:& a^{\wedge }{a}^{\wedge }=a{a}^T-I\\ 式2:& a^{\wedge }{a}^{\wedge }{a}^{\wedge }=a^{\wedge }(a{a}^T-I)=-a^{\wedge }\end{array}$$

指数映射

对指数映射进行Taylor展开并将上述等式代入：
$$\begin{array}{rl}exp({\varphi }^{\wedge })& =exp(\theta a^{\wedge })=\sum _{n=0}^{\infty }\frac{1}{n!}(\theta a^{\wedge }{)}^n\\ 1:& =I+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }+\frac{1}{3!}{\theta }^3{a}^{\wedge }{a}^{\wedge }{a}^{\wedge }+\frac{1}{4!}{\theta }^4(a^{\wedge }{)}^4+\cdots \\ 2:& =(a{a}^T-a^{\wedge }{a}^{\wedge })+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }-\frac{1}{3!}{\theta }^3{a}^{\wedge }-\frac{1}{4!}{\theta }^4{a}^{\wedge }{a}^{\wedge }+\cdots \\ 3:& =a{a}^T+(\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdots )a^{\wedge }-(1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdots )a^{\wedge }{a}^{\wedge }\\ 4:& =(I+a^{\wedge }{a}^{\wedge })+\sin \theta a^{\wedge }-\cos \theta a^{\wedge }{a}^{\wedge }\\ 5:& =(1-\cos \theta )a^{\wedge }{a}^{\wedge }+I+\sin \theta a^{\wedge }\\ 6:& =(1-\cos \theta )(a{a}^T-I)+I+\sin \theta a^{\wedge }\\ 7:& =\cos \theta I+(1-\cos \theta )a{a}^T+\sin \theta a^{\wedge }\end{array}$$
上述计算过程的处理思路如下：

• 第一步：泰勒展开

• 第二步：将式1代入替换第一步中的$I$；将式2代入替换$a^{\wedge }{a}^{\wedge }{a}^{\wedge }$

• 第三步：对第二步进行整理

• 第四步：将式1代入替换第三步中的$a{a}^T$；将三角函数的泰勒展开形式写回三角函数形式：
  $$\begin{array}{rl}\sin \theta & =\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdots \\ \cos \theta & =1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdots \end{array}$$

• 第五步：对第四步进行整理

• 第六步：将式1代入替换第五步中$a^{\wedge }{a}^{\wedge }$

• 第七步：对第六步进行整理

最终得到李代数$so(3)$到李群$SO(3)$的指数映射：
$$exp({\varphi }^{\wedge })=exp(\theta a^{\wedge })=\cos \theta I+(1-\cos \theta )a{a}^T+\sin \theta a^{\wedge }$$
该式被称为罗德里格斯公式，李代数$so(3)$的物理意义就是旋转向量。

对数映射

由$SO(3)$到$so(3)$的对数映射如下：
$$\varphi =\ln (R{)}^{\vee }=(\sum _{n=0}^{\infty }\frac{(-1{)}^n}{n+1}(R-I{)}^{n+1}{)}^{\vee }$$
对数映射实现由旋转矩阵到旋转向量的转换，可使用刚体变换中计算方式，对指数映射两侧求迹从而简化计算：
$$\theta =\arccos \frac{tr(R)-1}{2}Rn=n$$

注意点

指数映射是一个满射，不是一个单射。也即每个$SO(3)$内的元素，都可以找到一个$so(3)$元素与之一一对应；但可能存在多个$so(3)$中的元素，对应到一个$SO(3)$中元素。

若将旋转角度固定至$\pm \pi$中，则可认为李群、李代数中元素一一对应。

李群$SE(3)$李代数$se(3)$

指数映射

由李代数$se(3)$到李群$SE(3)$的转换如下：
$$\begin{array}{rl}exp({\xi }^{\wedge })& =\left[\begin{array}{cc}{\sum }_{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n& {\sum }_{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n\rho \\ 0^T& 1\end{array}\right]\\ & \triangleq \left[\begin{array}{cc}R& J\rho \\ 0^T& 1\end{array}\right]\\ & =T\end{array}$$
式中$J$称为雅可比矩阵：
$$\begin{array}{rl}J=& \sum _{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n=\sum _{n=0}^{\infty }\frac{1}{(n+1)!}(\theta a^{\wedge }{)}^n\\ 1:=& I+\frac{1}{2!}\theta a^{\wedge }+\frac{1}{3!}{\theta }^2(a^{\wedge }{)}^2+\frac{1}{4!}{\theta }^3(a^{\wedge }{)}^3+\frac{1}{5!}{\theta }^4(a^{\wedge }{)}^4+\cdots \\ 2:=& I+\frac{1}{\theta }(\frac{1}{2!}{\theta }^2{a}^{\wedge }+\frac{1}{3!}{\theta }^3(a^{\wedge }{)}^2+\frac{1}{4!}{\theta }^4(a^{\wedge }{)}^3+\frac{1}{5!}{\theta }^5(a^{\wedge }{)}^4+\cdots )\\ 3:=& I+\frac{1}{\theta }(\frac{1}{2!}{\theta }^2{a}^{\wedge }+\frac{1}{3!}{\theta }^3(a^{\wedge }{)}^2-\frac{1}{4!}{\theta }^4{a}^{\wedge }-\frac{1}{5!}{\theta }^5(a^{\wedge }{)}^2+\cdots )\\ 4:=& I+\frac{1}{\theta }(\frac{1}{2!}{\theta }^2-\frac{1}{4!}{\theta }^4+\cdots )a^{\wedge }+\frac{1}{\theta }(\frac{1}{3!}{\theta }^3-\frac{1}{5!}{\theta }^5+\cdots )(a^{\wedge }{)}^2\\ 5:=& I+\frac{1}{\theta }(1-\cos \theta )a^{\wedge }+\frac{1}{\theta }(\theta -\sin \theta )(a^{\wedge }{)}^2\\ 6:=& I+\frac{1}{\theta }(1-\cos \theta )a^{\wedge }+\frac{1}{\theta }(\theta -\sin \theta )(a{a}^T-I)\\ 7:=& \frac{\sin \theta }{\theta }I+(1-\frac{\sin \theta }{\theta })a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }\end{array}$$
上述计算过程的处理思路如下：

• 第一步：泰勒展开

• 第二步：除单位阵$I$外其余项提出一个因子$\frac{1}{\theta }$

• 第三步：将式2代入代替$(a^{\wedge }{)}^3$

• 第四步：对第三步进行整理，将有共同项的写在一起

• 第五步：将三角函数的泰勒展开进行整理后代入上式：
  $$\begin{array}{rl}\cos \theta & =1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdots \\ 1-\cos \theta & =\frac{1}{2!}{\theta }^2-\frac{1}{4!}{\theta }^4+\cdots \\ & \\ \sin \theta & =\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdots \\ \theta -\sin \theta & =\frac{1}{3!}{\theta }^3-\frac{1}{5!}{\theta }^5+\cdots \end{array}$$

• 第六步：将式1代入代替$(a^{\wedge }{)}^2$

• 第七步：对第六步进行整理

由此得到雅可比矩阵的表达式：
$$J=\frac{\sin \theta }{\theta }I+(1-\frac{\sin \theta }{\theta })a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }$$

对数映射

从$SE(3)$到$se(3)$的转换，如下：
$$\xi =\ln (T{)}^{\vee }$$
在进行实际转换时，使用对数映射较为复杂。一般用$T$左上角旋转矩阵$R$求解旋转向量；再由右侧平移向量计算平移部分：
$$t=J\rho$$

总结