线性规划LP和混合整数规划MIP基础知识
如果你刚刚入门线性规划,对于线性规划的基本原理、概念、术语,以及 Gurobi 内部的核心算法不了解的话,请花费 10分钟时间,阅读以下两个科普文章。如果对于英文不熟练的话,可以采用谷歌浏览器,然后选择翻译为中文。
LP 基础:https://www.gurobi.com/resource/linear-programming-basics/
MIP 基础: https://www.gurobi.com/resource/mip-basics/
(参考翻译:cplex整数规划_Branch-and-Cut 解混合整数规划(MIP)_彷徨的牛的博客-CSDN博客)
一.优化基础
优化中非常重要的3个要素,分别是:决策变量、约束条件、和目标函数。
根据3个要素的不同,可以将问题划分为多种不同的类型。LP线性规划和MIP混合整数规划就是其中的两类。
二.LP线性规划
决策变量没有要求;约束条件是线性的;目标函数是线性的。
![]()
![]()
在生活中非常的常见。整数规划也在生活中非常常见,解决时与线性规划有密切的关系,可以说线性规划是基础,也是求解发展最成熟的一类模型。
解决LP的第一算法是George Dantzig in 1947提出的单纯形法。显着的,这65岁的旧算法仍然是今天解决这些问题的最有效和最可靠的方法之一。 单纯形方法的主要替代方法是内点法。 这种方法历史悠久,但其近期受欢迎程度是由于Karmarkar’s 1984的1984年多项式复杂性证明。 内点法从计算机架构中的最近进步中显着受益,包括引入多核处理器和SIMD指令集,并且通常被认为比Simplex从头开始解决LP问题更快。 然而,不同LP模型以及使用LP的许多不同方式,意味着在实践中两种算法都没有主导(并没有明确的谁最快),因此两者在计算线性规划中都很重要。
根据对Bench mark数据集的测试,并没有哪种求解器稳定占优。这主要有三个原因所影响(后两点不是特别明白):
(1)稀疏矩阵ASparse Linear Algebra,约束矩阵A非常稀疏,即包含非常少的非0项。(例如运输问题,单模矩阵)。
(2)数值处理误差。
(3)开发出不同的启发式策略(如单纯形法,每次选择一个进基变量,进基变量的不同会导致最终处理效率的不同),这个有赖于经验。
三.MIP混合整数规划(可以和IP整数规划互相转换,本质是求解同一类问题)
一些或全部的决策变量必须为整数,或者0-1变量(integrality constraints)
Gurobi MIP求解器还可以解决具有二次目标和/或二次约束的模型:
MIP模型具有二次目标但没有二次约束称为混合整数二次编程(MIQP)问题。具有二次约束的MIP模型称为混合整数二次约束编程(MIQCP)问题。没有任何二次特征的模型通常被称为混合整数线性编程(MILP)问题。
以下介绍求解MILP的算法:
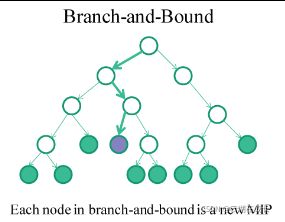
通常使用基于LP的分支定界算法 branch-and-bound来解决。
思路很简单,可以看运筹学教材。就是不断分支,不断定界的过程。当松弛问题没有可行解或整数解大于当前下界(默认是最小值问题),那么就剪断此支(incumbent需要分支的节点;fathomed不必再分支的节点。)
整数解为上界,不断更换。同时有个有效下界,不断缩小上下界Gap的过程,就是寻优的过程。当上下界相等,那么就找到了最优解。
以下4种方法可以提高MIP的求解效率:
Presolve, Cutting Planes, Heuristics, Parallelism
(1)预处理Presolve
是指在分支定界之前进行的操作。可以减少问题的规模,或者可以收紧问题的formulation。简而言之,就是预处理使得问题更易求解。
(2)割平面Cutting Planes
也是收紧约束的一种方法,是通过移除一些分数解的方式实现的(没有任何副作用),比分支定界有效。
割平面非常有用。但是不把所有割平面都作为约束加在约束中主要有两个原因:第一,找到全部的割平面太难了,或者代价非常昂贵;第二,有的割平面加进去,反而不利于求解。 我们想加入的是,利于我们求解的割平面。
(3)启发式算法Heuristics
启发式算法的优点是快,能够快速地给出一个可行解。当求解MIP问题用户对时间要求严格时,启发式的意义就体现出来了。启发式算法给的可行解作为上界,松弛的问题很容易超过它,那么这一支就可以被砍掉了。
主要是提升求解效率,分得支更少。
(4)平行求解Parallelism
除了以上4种技术外,solver还提供了其它的一系列求解技巧。这些技巧的最终目的都是为了减少分支树的求解规模。
这些技巧通常可以通过gurobi的一些参数进行设置和调节。
参考:
优化|用Branch-and-Cut 解混合整数规划
混合整数规划 Branch-and-Cut求解方法