融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法
文章目录
- 一、理论基础
-
- 1、阿奎拉鹰优化算法
- 2、哈里斯鹰优化算法
- 3、动态反向学习策略
- 4、融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法
-
- (1)改进混合算法步骤
- (2)计算复杂度分析
- 二、实验仿真与分析
- 三、参考文献
一、理论基础
1、阿奎拉鹰优化算法
请参考这里。
2、哈里斯鹰优化算法
请参考这里。
3、动态反向学习策略
对于元启发式优化算法来说,种群初始化往往是在搜索空间内随机生成的,只能保证种群在搜索空间内的分散程度,无法保证初始解的质量。然而,研究表明初始化的好坏将直接影响算法的收敛速度和解的精度。基于此问题,国内外学者将多种策略引入初始化部分,以提高算法初始化性能,常见的有混沌初始化、反向学习和柯西随机生成等。本文引入动态反向学习策略,提高初始化解的质量,计算方法如下为: X DOBL = X init + r 1 × ( r 2 × ( L B + U B − X init ) − X init ) (1) X_{\text{DOBL}}=X_{\text{init}}+r_1\times\left(r_2\times\left(LB+UB-X_{\text{init}}\right)-X_{\text{init}}\right)\tag{1} XDOBL=Xinit+r1×(r2×(LB+UB−Xinit)−Xinit)(1)其中, X init X_{\text{init}} Xinit代表通过随机生成的初始化种群; r 1 r_1 r1与 r 2 r_2 r2均为分布在0到1之间的随机数。首先,算法分别生成原始初始化种群 X init X_{\text{init}} Xinit与反向初始种群 X DOBL X_{\text{DOBL}} XDOBL,然后将两个种群合并为新种群 X new = { X DOBL ∪ X init } X_{\text{new}}=\{X_{\text{DOBL}}\cup X_{\text{init}}\} Xnew={XDOBL∪Xinit}。计算新种群的适应度值,并利用贪婪策略使种群内部充分竞争,选取最佳的 N N N个个体作为初始化种群。通过此方法能够让种群更快的靠近最优解,从而提升算法的收敛速度。
4、融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法
(1)改进混合算法步骤
改进混合算法DAHHO步骤如下:
步骤1. 初始化种群,计算动态反向学习种群,根据贪婪策略保留较优个体进入主程序迭代。
步骤2. 计算种群适应度值,记录较优个体。
步骤3. 如果 ∣ E ∣ ≥ 1 |E|\geq1 ∣E∣≥1,个体随机选择式(1)或式(3)开始探索行为。
步骤4. 如果 ∣ E ∣ < 1 |E|<1 ∣E∣<1,种群根据逃逸猎物能量值与适应度值选择开发策略。
\quad\quad 策略1. 软包围。当 r 16 ≥ 0.5 r_{16}\geq0.5 r16≥0.5且 ∣ E ∣ ≥ 0.5 |E|\geq0.5 ∣E∣≥0.5,子群个体采用式(11)更新位置。
\quad\quad 策略2. 硬包围。当 r 16 ≥ 0.5 r_{16}\geq0.5 r16≥0.5且 ∣ E ∣ < 0.5 |E|<0.5 ∣E∣<0.5,子群个体采用式(14)更新位置。
\quad\quad 策略3. 渐进式快速俯冲软包围。当 r 16 < 0.5 r_{16}<0.5 r16<0.5且 ∣ E ∣ ≥ 0.5 |E|\geq0.5 ∣E∣≥0.5,子群个体采用式(15, 16, 17)更新位置。
\quad\quad 策略4. 渐进式快速俯冲硬包围。当 r 16 < 0.5 r_{16}<0.5 r16<0.5且 ∣ E ∣ < 0.5 |E|<0.5 ∣E∣<0.5,子群个体采用式(16, 17, 18)更新位置。
步骤5. 判断程序是否满足终止条件,满足则跳出循环,否则返回步骤2。
步骤6. 输出最佳位置及适应度值。
(2)计算复杂度分析
DAHHO计算复杂度主要取决于以下三个过程:动态反向学习初始化,适应度评估以及种群位置更新。假设种群规模为 N N N,则初始化计算复杂度为 O ( 2 × N ) O(2\times N) O(2×N)。评价最佳位置以及更新种群位置向量的计算复杂度为 O ( N × T + N × T × D ) O(N\times T+N\times T\times D) O(N×T+N×T×D)。综上所述,DAHHO的计算复杂度为 O ( N × ( 2 + T + T × D ) ) O(N\times (2+T+T\times D)) O(N×(2+T+T×D))。考虑到NFL定理,增加一些额外的计算复杂度来获取更好的解决方案是可取的。
二、实验仿真与分析
将DAHHO与AO、HHO、SSA、WOA、SCA、MVO和GWO进行对比,以常用23个测试函数中的F4、F5(单峰函数/30维)、F11、F12(多峰函数/30维)、F19、F20(固定维度多峰函数/3维、6维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
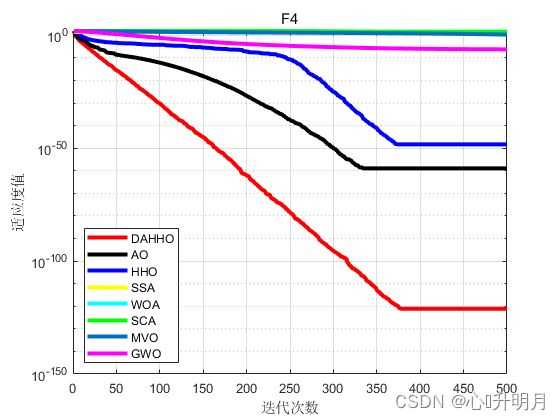
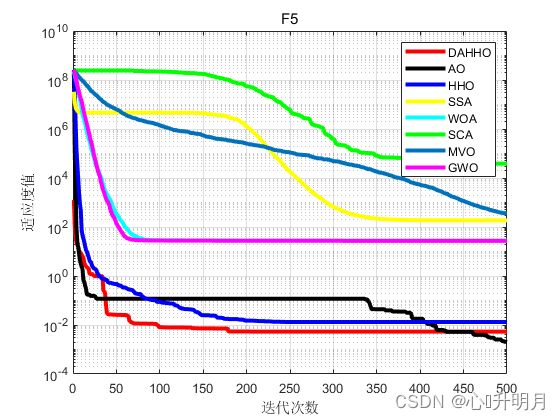


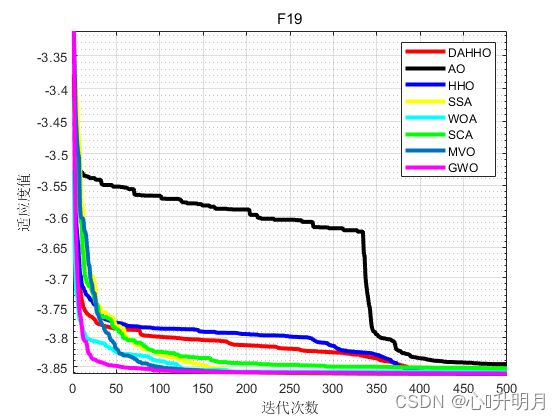

函数:F4
DAHHO:最差值: 1.1448e-120, 最优值: 2.5451e-132, 平均值: 7.9133e-122, 标准差: 2.2808e-121, 秩和检验: 1
AO:最差值: 3.4883e-58, 最优值: 2.2647e-79, 平均值: 1.1629e-59, 标准差: 6.3687e-59, 秩和检验: 3.0199e-11
HHO:最差值: 1.486e-47, 最优值: 1.2658e-57, 平均值: 5.0871e-49, 标准差: 2.7106e-48, 秩和检验: 3.0199e-11
SSA:最差值: 18.3308, 最优值: 6.6736, 平均值: 11.3412, 标准差: 2.7763, 秩和检验: 3.0199e-11
WOA:最差值: 83.3169, 最优值: 2.0983, 平均值: 45.4455, 标准差: 28.4264, 秩和检验: 3.0199e-11
SCA:最差值: 62.5664, 最优值: 18.2128, 平均值: 36.1108, 标准差: 10.8684, 秩和检验: 3.0199e-11
MVO:最差值: 5.1286, 最优值: 1.0596, 平均值: 2.2109, 标准差: 1.0788, 秩和检验: 3.0199e-11
GWO:最差值: 3.067e-06, 最优值: 1.0531e-07, 平均值: 6.6996e-07, 标准差: 7.8541e-07, 秩和检验: 3.0199e-11
函数:F5
DAHHO:最差值: 0.089985, 最优值: 1.5822e-06, 平均值: 0.0053932, 标准差: 0.016638, 秩和检验: 1
AO:最差值: 0.01463, 最优值: 7.7425e-05, 平均值: 0.0020187, 标准差: 0.0030768, 秩和检验: 0.40354
HHO:最差值: 0.087886, 最优值: 3.0252e-05, 平均值: 0.013273, 标准差: 0.01773, 秩和检验: 4.084e-05
SSA:最差值: 1005.3687, 最优值: 25.7616, 平均值: 186.3118, 标准差: 223.5295, 秩和检验: 3.0199e-11
WOA:最差值: 28.7797, 最优值: 27.2047, 平均值: 28.0633, 标准差: 0.4671, 秩和检验: 3.0199e-11
SCA:最差值: 278965.312, 最优值: 186.8166, 平均值: 38459.3734, 标准差: 75461.0467, 秩和检验: 3.0199e-11
MVO:最差值: 2259.7661, 最优值: 36.3849, 平均值: 359.6763, 标准差: 562.5061, 秩和检验: 3.0199e-11
GWO:最差值: 28.7643, 最优值: 26.0273, 平均值: 27.1439, 标准差: 0.85692, 秩和检验: 3.0199e-11
函数:F11
DAHHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
AO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SSA:最差值: 0.044636, 最优值: 0.0001397, 平均值: 0.015584, 标准差: 0.010806, 秩和检验: 1.2118e-12
WOA:最差值: 0.28789, 最优值: 0, 平均值: 0.014684, 标准差: 0.058636, 秩和检验: 0.1608
SCA:最差值: 1.3721, 最优值: 0.18433, 平均值: 0.89206, 标准差: 0.30749, 秩和检验: 1.2118e-12
MVO:最差值: 1.0033, 最优值: 0.66443, 平均值: 0.86449, 标准差: 0.084799, 秩和检验: 1.2118e-12
GWO:最差值: 0.034059, 最优值: 0, 平均值: 0.0056433, 标准差: 0.010229, 秩和检验: 0.002788
函数:F12
DAHHO:最差值: 9.2903e-06, 最优值: 2.3631e-09, 平均值: 1.0596e-06, 标准差: 1.9276e-06, 秩和检验: 1
AO:最差值: 9.0249e-06, 最优值: 8.2443e-09, 平均值: 2.4373e-06, 标准差: 2.5738e-06, 秩和检验: 0.004033
HHO:最差值: 2.2955e-05, 最优值: 2.5543e-12, 平均值: 5.758e-06, 标准差: 6.6168e-06, 秩和检验: 0.00010407
SSA:最差值: 21.4492, 最优值: 2.6682, 平均值: 8.2306, 标准差: 4.5551, 秩和检验: 3.0199e-11
WOA:最差值: 0.10879, 最优值: 0.0036595, 平均值: 0.025439, 标准差: 0.021631, 秩和检验: 3.0199e-11
SCA:最差值: 3425121.4295, 最优值: 1.5843, 平均值: 205825.9541, 标准差: 759498.7867, 秩和检验: 3.0199e-11
MVO:最差值: 4.4777, 最优值: 0.35481, 平均值: 2.2656, 标准差: 1.2455, 秩和检验: 3.0199e-11
GWO:最差值: 0.086289, 最优值: 0.011838, 平均值: 0.044186, 标准差: 0.021927, 秩和检验: 3.0199e-11
函数:F19
DAHHO:最差值: -3.8619, 最优值: -3.8628, 平均值: -3.8627, 标准差: 0.00017311, 秩和检验: 1
AO:最差值: -3.7056, 最优值: -3.8627, 平均值: -3.8458, 标准差: 0.034729, 秩和检验: 3.1589e-10
HHO:最差值: -3.8627, 最优值: -3.8628, 平均值: -3.8628, 标准差: 1.3823e-05, 秩和检验: 0.48252
SSA:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.4013e-10, 秩和检验: 3.0199e-11
WOA:最差值: -3.8477, 最优值: -3.8628, 平均值: -3.8587, 标准差: 0.0047386, 秩和检验: 3.4742e-10
SCA:最差值: -3.8411, 最优值: -3.8585, 平均值: -3.8528, 标准差: 0.0029211, 秩和检验: 3.0199e-11
MVO:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 3.5765e-06, 秩和检验: 0.00018916
GWO:最差值: -3.8549, 最优值: -3.8628, 平均值: -3.8618, 标准差: 0.0020159, 秩和检验: 4.7445e-06
函数:F20
DAHHO:最差值: -3.2014, 最优值: -3.322, 平均值: -3.3059, 标准差: 0.04134, 秩和检验: 1
AO:最差值: -3.0759, 最优值: -3.3193, 平均值: -3.2461, 标准差: 0.077339, 秩和检验: 4.6856e-08
HHO:最差值: -3.1837, 最优值: -3.322, 平均值: -3.2848, 标准差: 0.057667, 秩和检验: 0.71719
SSA:最差值: -3.1615, 最优值: -3.322, 平均值: -3.2327, 标准差: 0.060087, 秩和检验: 0.013272
WOA:最差值: -3.1106, 最优值: -3.3219, 平均值: -3.2554, 标准差: 0.080892, 秩和检验: 1.8731e-07
SCA:最差值: -1.9171, 最优值: -3.1315, 平均值: -2.9316, 标准差: 0.24295, 秩和检验: 3.0199e-11
MVO:最差值: -3.191, 最优值: -3.322, 平均值: -3.2657, 标准差: 0.06121, 秩和检验: 0.43764
GWO:最差值: -3.1372, 最优值: -3.322, 平均值: -3.2796, 标准差: 0.067659, 秩和检验: 0.0066689
结果表明引入动态反向学习的混合算法收敛性能更佳,能够有效求解优化问题。
三、参考文献
[1] 贾鹤鸣, 刘庆鑫, 刘宇翔, 等. 融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法[J/OL]. 智能系统学报: 1-13 [2022-09-29].