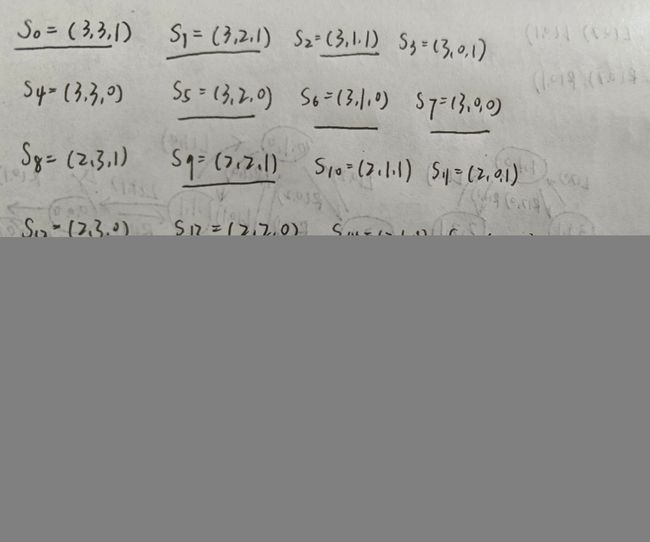用状态空间方法求解修道士与野人问题
目录
一、状态空间表示法回顾
1.问题状态空间的构成
2.用状态空间表示问题的步骤
二、使用状态空间法求解修道士与野人问题
1.问题描述
2.状态空间求解步骤
总结
一、状态空间表示法回顾
状态空间表示法就是用状态空间对问题进行表示。
1.问题状态空间的构成
状态:
描述问题求解过程中不同时刻状况的数据结构,一般用一组变量的有序集合组成。
如Q=(q0,q1,q2···)当给每个变量以确定的值时,就得到一个具体的状态。
算符:
引起状态发生变化,使问题由一个状态变为另一个状态的操作成为算符。
状态空间:
由初始状态集合S+算符集合F+目标状态集合G构成的三元组:(S,F,G)
状态空间的图示形式成为状态空间图,节点为状态,有向边为算符。
问题的解:
从初始状态集S出发,经过一系列算符运算,到达目标状态。由初始状态到目标状态所用的算符序列构成问题的一个解。
2.用状态空间表示问题的步骤
①定义状态的描述形式。
②用定义的状态描述形式,把所有可能的状态描述出来,并确定问题的初始状态和目标状态集合描述。
③定义一组算符。使利用这组算符可从一种状态转为另一种状态。
二、使用状态空间法求解修道士与野人问题
1.问题描述
设有3个修道士和3个野人来到河边,打算用一条船从河的左岸渡到河的右岸。
但该船每次只能装载2个人,在任何岸边野人的数目都不得超过修道士的人数,否则修道士就会被野人吃掉。
假设野人服从任何一种过河安排,如何规划过河计划才能把所有人安全地渡过河去?
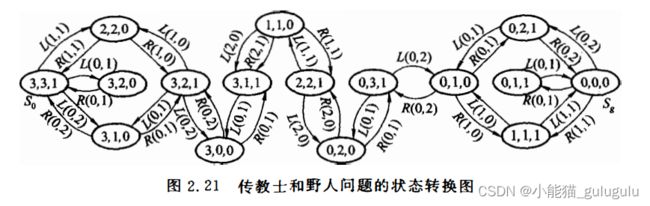
用状态空间表示法表示修道士和野人的问题,画出状态空间图。
2.状态空间求解步骤
第一步,定义状态的描述形式:
第二步,用定义的状态描述表示所有可能的状态:
其中,因为题中的安全约束条件,无论左岸还是右岸,野人数目均不能超过修道士人数,因此其中只有20个状态是合法的,用下划线表示。
列出的全部状态,初始状态和目标状态用下划线画出:
判断是否为合法状态的方法(自己瞎想出来的):
判断某个节点是否合法,画出状态对应的图示,看通过船每次运不超过2个人这种操作(其实就是算符)能否回到初始状态或到达目标状态,因为初始状态和目标状态一定合法。
一定不合法的状态:
在左岸或右岸野人数量>修道士数量
所有的人都在一边,而船却在另一边,没人能把船开过来,如(3,3,0)
以状态(3,2,1)为例:
最后用下划线标出所有的合法状态:
第三步,定义算符:
L(i,j):表示把i个修道士和j个野人从左岸运输到右岸
R(i,j):表示把i个修道士和j个野人从右岸运输到左岸
注意:i+j≤2
因此全部的算符为:L(1,0) L(2,0) L(1,1) L(0,1) L(0,2)
R(1,0) R(2,0) R(1,1) R(0,1) R(0,2)
至此(S,F,G)构建完成,画出状态空间图即可。(在画图的过程中,画出图示更加清楚)
画图的大致方法:
1.从初始状态开始,遍历算符,得出经过算符运算后的状态
2.观察运算后的状态是否为合法状态,若合法,则记录下来画在图中
3.将初始状态和运算后的状态通过有向边连接,有向边上就是刚才用到的算符
tips:画了一个方向的有向边,其实返回方向的有向边也可以画出来了。
4.不断对新生成的状态进行算符计算,得到目标状态后也要计算一下能够生成的状态,最后停止。
总结
很多方法都是我自己看着答案思考出来的,方法看着比较笨,希望大家多多指正。