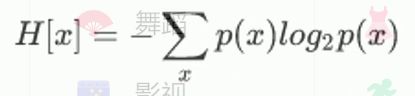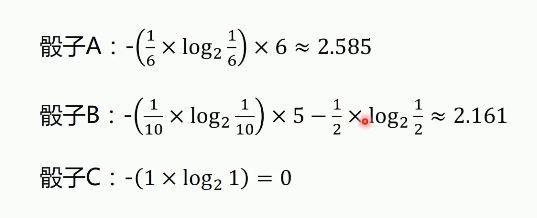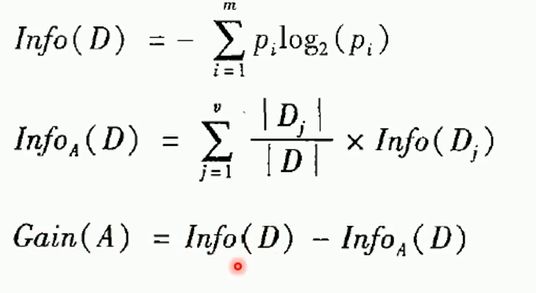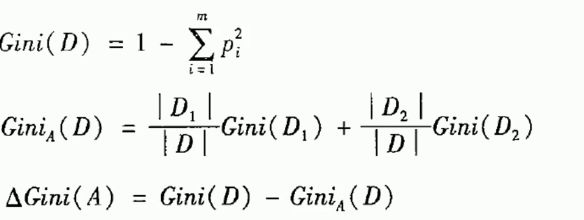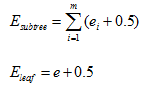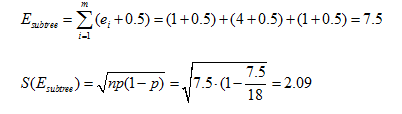机器学习笔记-决策树

决策树（Decision Tree）简介

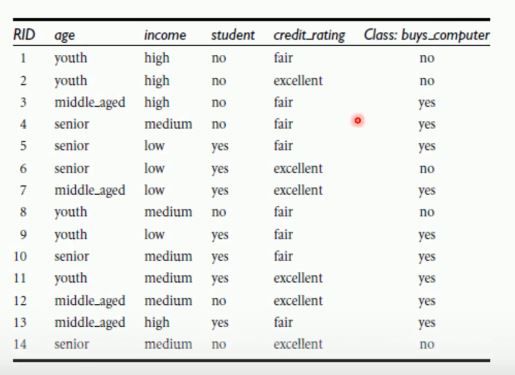
决策树是一种分类和回归算法。比较适合分析离散数据。如果是连续数据要先转成离散数据在做分析。

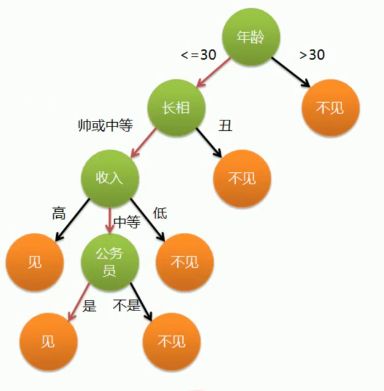
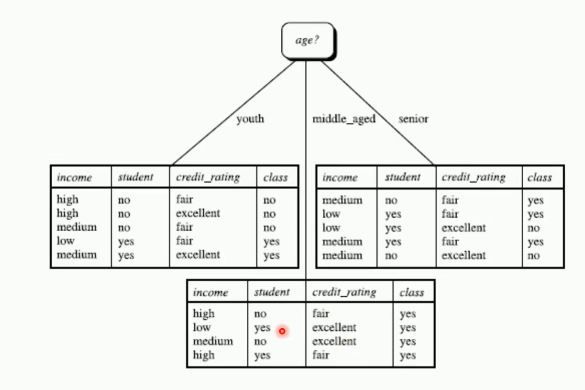
决策树简单例子

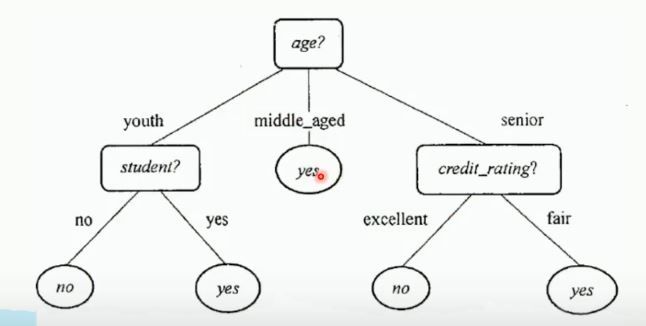
根据以上表格可以根据年龄为根节点画出的决策树如下所示：

也可以把收入和是否为学生等来作为根节点来画出决策树，因此决策树不唯一。

熵（Entropy）概念

1948年，香农提出了“信息熵”的概念。一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息。信息量的度量就是等于不确定性的多少。

信息熵公式如下所示

p：代表概率；x:代表每种情况的可能性

例子：

其结果如下所示：

ID3算法

决策树会选择最大化信息增益来对结点进行划分，信息增益计算：

Info(D)最后结果的每个概率

利用ID3算法来计算例题：

选择信息增益最大的作为根节点，确定根节点后在计算其余参数的信息增益。

ID3算法的缺点：计算信息增益的时更倾向于分支多的参数作为节点。

C4.5算法

C4.5是ID3算法的改进，在ID3算法的基础上添加了一个增益率。添加了增益率之后，优化了ID3的缺点。

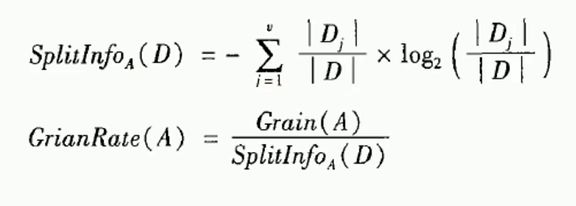
ID3算法实例：

数据集为例子中是否买电脑的例子，例子数据如下图所示：

导入包：

from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn import preprocessing
from sklearn.preprocessing import LabelBinarizer
import csv

读入数据：

Dtree=open(r'AllElectronics.csv','r')#可以读取字符类型
reader=csv.reader(Dtree)
#获取第一行数据
headers=reader.__next__()#第一行
print(headers)
#定义两个列表
featureList=[]#特征
labelList=[]#标签
for row in reader:
    #把label 存入list
    labelList.append(row[-1])#保存no or yes
    rowDict={}
    for i in range(1,len(row)-1):
        #建立一个数据字典
        rowDict[headers[i]]=row[i]
    #把数据字典存入list
    featureList.append(rowDict)
print(featureList)

把数据转化为0、1格式：

#把数据转换成01表示
vec=DictVectorizer()#特征提取
x_data=vec.fit_transform(featureList).toarray()#转化为01形式
print('x_data:'+str(x_data))
#打印属性名称
print(vec.get_feature_names())
print("labelList:"+str(labelList))
#把标签转化为01表示
lb=LabelBinarizer()
y_data=lb.fit_transform(labelList)
print("y_data:"+str(y_data))

创建决策树模型：

#创建决策树模型
model=tree.DecisionTreeClassifier(criterion='entropy')#默认基尼指数
#输入数据建立模型
model.fit(x_data,y_data)

测试和预测：

x_test=x_data[0]
print('x_test:'+str(x_test))
predict=model.predict(x_test.reshape(1,-1))
print("predict:"+str(predict))

导出决策树：

import graphviz
dot_data=tree.export_graphviz(model,
                             out_file=None,
                             feature_names=vec.get_feature_names(),
                             class_names=lb.classes_,
                             filled=True,
                             rounded=True,
                             special_characters=True)
graph=graphviz.Source(dot_data)
graph.render('computer')

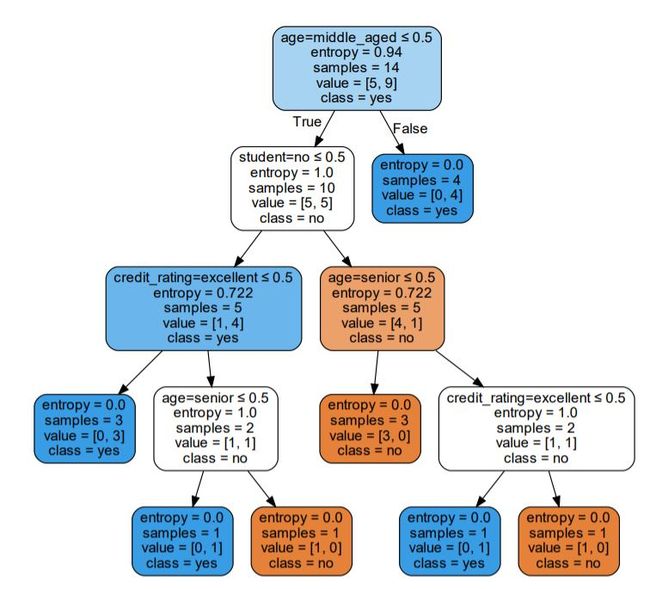
结果如下所示：

CART算法

CART决策树的生成就是递归地构建二叉树的过程

CART用基尼（Gini）系数最小化准则来进行特征的选择，生成二叉树

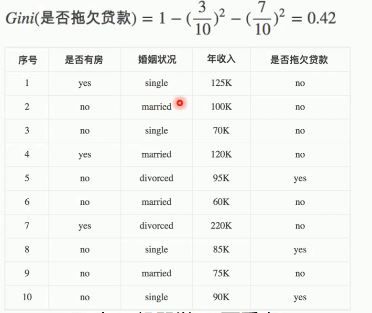
GIni系数计算：

CART举例

分别计算它们的Gini系数增益，取Gini系数增益值最大的属性作为决策树的根节点属性，根节点的Gini系数：

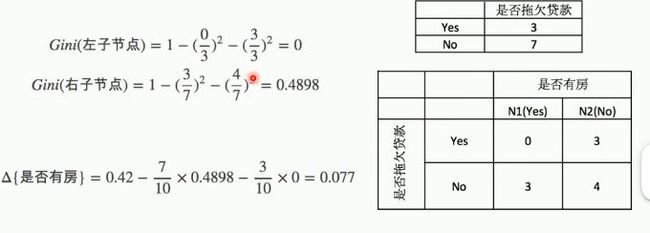
根据是否有房来进行划分时，Gini系数增益计算：（左子节点代表yes，右zi节点代表no）

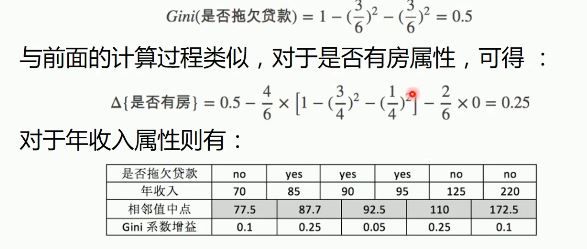
计算婚姻的状况，由于CART算法是一个二叉树，因此需要把婚姻状态分为两种，如下所示：

根据年收入进行划分时，由于年收入是一个连续性的数据。首要是要将年收入进行排序，再计算相邻值的中点（平均值），再分别计算Gini指数，其结果如下所示：

由于婚姻状态和年收入属性的最大Gini指数都为0.12，则假设选择婚姻状况作为根节点。接下来，使用同样的方法，分别计算剩下的属性，其根节点的Gini系数为：

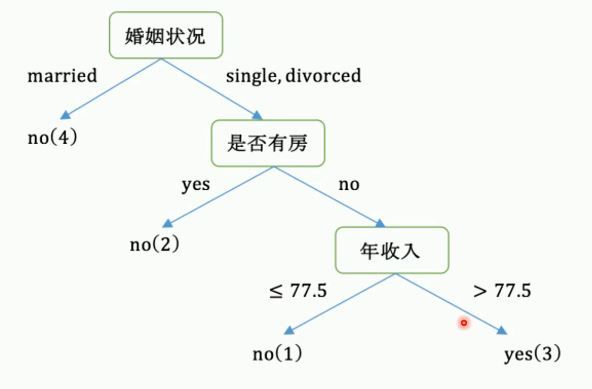
最后构建的CART决策树如下所示：

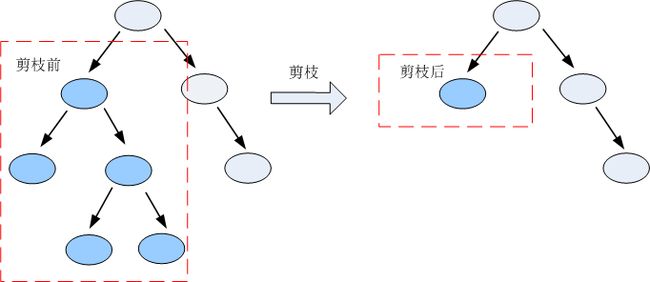
剪枝

剪枝是将一颗子树的子节点全部删除，根节点作为叶子节点，具体如下图所示：

为什么要剪枝？

决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。

考虑极端的情况，如果我们令所有的叶子节点都只含有一个数据点，那么我们能够保证所有的训练数据都能准确分类，但是很有可能得到高的预测误差，原因是将训练数据中所有的噪声数据都”准确划分”了，强化了噪声数据的作用。

剪枝修剪分裂前后分类误差相差不大的子树，能够降低决策树的复杂度，降低过拟合出现的概率。

怎样剪枝？

两种实现方案：先剪枝和后剪枝

先剪枝：说白了通过提前停止树的构建而对树剪枝，一旦停止，该节点就作为叶子节点了。

停止决策树最简单的方法有：

• 定义一个高度，当决策树达到该高度时就停止决策树的生长
• 达到某个节点的实例具有相同的特征向量，及时这些实例不属于同一类，也可以停止决策树的生长。这个方法对于处理数据的数据冲突问题比较有效。
• 定义一个阈值，当达到某个节点的实例个数小于阈值时就可以停止决策树的生长
• 定义一个阈值，通过计算每次扩张对系统性能的增益，并比较增益值与该阈值大小来决定是否停止决策树的生长

后剪枝：是在决策树生长完成之后再进行剪枝的过程，后剪枝主要有错误率降低剪枝(REP)、悲观剪枝(PEP)和代价复杂度剪枝(CCP)三种方法。

1、REP-错误率降低剪枝

顾名思义，该剪枝方法是根据错误率进行剪枝，如果一棵子树修剪前后错误率没有下降，就可以认为该子树是可以修剪的。

REP剪枝需要用新的数据集，原因是如果用旧的数据集，不可能出现分裂后的错误率比分裂前错误率要高的情况。由于使用新的数据集没有参与决策树的构建，能够降低训练数据的影响，降低过拟合的程度，提高预测的准确率。

2、PEP-悲观剪枝

悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话，则进行剪枝。怎样才算是没有影响？如果剪枝后的误差小于剪枝前经度的上限，则说明剪枝后的效果与剪枝前的效果一致，此时要进行剪枝。

进行剪枝必须满足以下条件：

其中：

表示剪枝前子树的误差

表示剪枝后节点的误差

两者的计算公式如下所示：

，其中
，其中N为子树的数据量。

上述公式中，0.5表示修正因子。由于子节点是父节点进行分裂的结果，从理论上讲，子节点的分类效果总比父节点好，分类的误差更小，如果单纯通过比较子节点和父节点的误差进行剪枝就完全没有意义了，因此对节点的误差计算方法进行修正。修正的方法是给每一个节点都加上误差修正因子0.5，在计算误差的时候，子节点由于加上了误差修正因子，就无法保证总误差低于父节点。

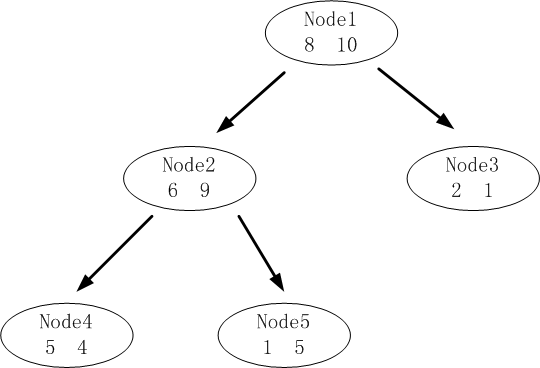
例如：

所以应该进行剪枝。

3、CCP-代价复杂度剪枝

代价复杂度选择节点表面误差率增益值最小的非叶子节点，删除该非叶子节点的左右子节点，若有多个非叶子节点的表面误差率增益值相同小，则选择非叶子节点中子节点数最多的非叶子节点进行剪枝。

CART算法实现

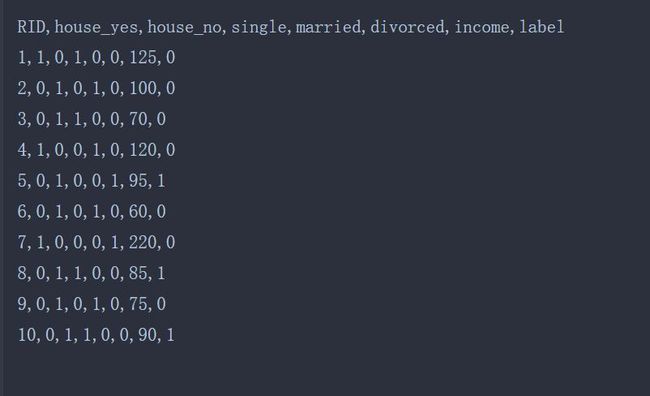
数据集为例子中的数据。

需要进行数据预处理，将文字设置为数字形式。其结果如下图所示：

导包：

from sklearn import tree
import numpy as np

载入数据：

data=np.genfromtxt("cart.csv",delimiter=",")
x_data=data[1:,1:-1]
y_data=data[1:,-1]

构建决策树:

model=tree.DecisionTreeClassifier() #不传递参数的话，默认就是CART算法
#输入数据建立模型
model.fit(x_data,y_data)

导出决策树：

import graphviz
dot_data=tree.export_graphviz(model,
                             out_file=None,
                             feature_names=['house_yes','house_no','single','married','divorced','income'],
                             class_names=['no','yes'],
                             filled=True,
                             rounded=True,
                             special_characters=True)
graph=graphviz.Source(dot_data)
graph.render('cart')

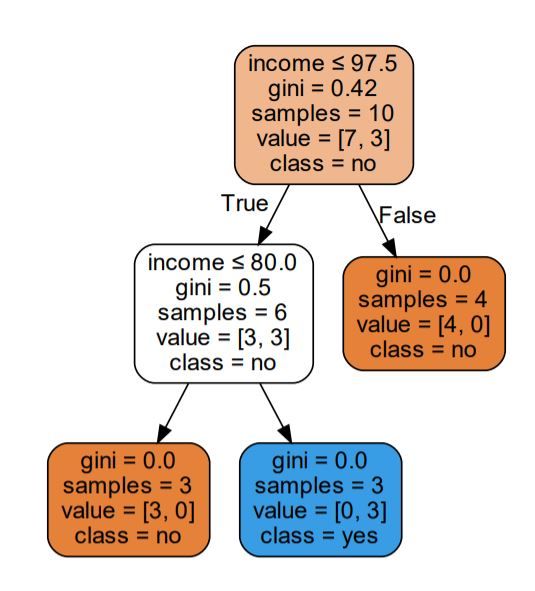
其结果如下图所示：

参考：https://www.cnblogs.com/mdumpling/p/8087396.html

参考：https://zhuanlan.zhihu.com/p/267368825

参考视频：https://www.bilibili.com/video/BV1Rt411q7WJ?p=47&vd_source=166e4ef02c5e9ffa3f01c2406aec1508