Wasserstein距离的直观解释
Wasserstein(EM)距离的易懂解释
最近在学习Wgan相关知识时,看到wasserstein距离的相关数学概念,表示非常懵逼,结合着李宏毅教授的网课,觉得理解了一点,但是还是不透彻,于是乎重新拾起概率论课本,仔细研究了一番,有以下直观的认识。
1.Wasserstein(Earth Move)距离的直观理解
所谓EM距离,就是衡量两个分部之间的差异的一种计算方法。即把一个分布变换成另外一个分布需要的能量。(老板要给建筑工人搞建筑发的工资)接下来我将通过一个小例子详细解释一下它。
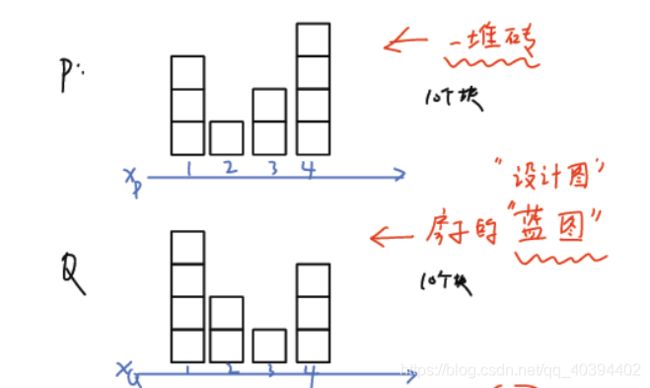
假设现在有两个分布,P和Q。
P的横轴为xp ,而Q的横轴为 xq 。纵轴表示在此横坐标上的y值。说了这么多,比较晦涩,我用一种直观的语言来描述一下。
P:大家好我是一堆砖头,长得像上图P的样子一样。
Q:大家好,我是一个房子(长得真草率)的设计图,P那堆砖头想变成我的样子。
好了,现在改如何把这堆砖头变成Q的样子呢?
(1)搬砖
如figure2所示,首先我们看两个轴,他们分别是xp 和xq ,其坐标和figure1一致,可以看到,Q的分布已经被我画成了虚线框,
虚线代表什么呢?他代表现在Q这个地方没有任何东西,只是一张设计图,我现在要做的,就是把P这堆砖头移动到这个虚线框里面。
接下来,我举例一种移动方法咯:
如figure2所示。已经被我打上了格子,每个格子的坐标都可以用xp 和xq 表示出来,比如说左上角的格子,它的坐标就是xp =1和xq=1,即(1,1);依次类推,其他格子的坐标也就可以知道了,右下角的格子坐标是(4,4)。
那么,格子里的数是什么呢?就是P要往Q对应位置移动砖头的个数!
举例,看(1,1)格子,里面红色的3就代表把P这堆砖头的xp =1处的3块砖头一起移动到Q设计图框架的xq=1处。 此时,Q的xq=1处的砖头还差一块。所以,我把P的xp =2处的一块紫色砖也移到了Q的xq=1处。于是乎Q设计图的xq=1位置已经搭建好了。
还是看上图,依次类推,我们可以按照同样的方法填充格子里的数字,最终结果就和figure2一样了!通过我们打工人的努力,所有的P砖头都被搬走了,并且形成了我们Q设计图里长得样子耶!
我们细心的观察,还会发现,表格里的数字,横着加起来是P对应位置的砖头数;纵着加起来就是Q对应位置的砖头数!(这好像没有什么好惊喜的,本来砖头就是这么搬的,所以加起来肯定是这样咯)
目前为止,我们的砖头已经搬完了,下一步就是算账了!
(2)工资
优秀的打工人已经把砖搬完了,建筑成了我们想要的Q的样子。现在好像缺点什么事情唉,要发工资!对,我们就是一个资本家,要给打工人发工资,唉,来算算工钱吧!
可以看到figure2中,我写了一个 γ \gamma γ ,这个 γ \gamma γ 是什么?他代表我们作为老板的一种策略:小李,你把这个搬到那!小王,你搬这个。。。具体到图上而言,就是我们的这个4x4的格子以及里面的数。它代表了我给打工人安排的搬砖的策略。
话不多说,上算账的公式!
B ( γ ) = ∑ x p , x q n γ ( x p , x q ) ∣ ∣ x p − x q ∣ ∣ 公 式 ( 1 ) B(\gamma)=\sum_{x_p,x_q}^{n}\gamma(x_p,x_q)||x_p-x_q|| \quad公式(1) B(γ)=xp,xq∑nγ(xp,xq)∣∣xp−xq∣∣公式(1)
好了,我们来看这个公式在说什么哈:
3
我们已经看到我这个黑心老板安排的搬砖策略了,就是figure2里面的那个4x4的表格。它就叫做 γ \gamma γ ,对于这个策略,我们要发的工资就是 B ( γ ) B(\gamma) B(γ) :
这个工资怎么算!就是按照公式1算,
很明显:
γ ( x p , x q ) \gamma(x_p,x_q) γ(xp,xq) 这一项,就是从表里面的对应坐标去找搬砖的块数。如 γ ( 1 , 1 ) \gamma(1,1) γ(1,1) 就是表里的左上角嘛,就是3!
∣ ∣ x p − x q ∣ ∣ ||x_p-x_q|| ∣∣xp−xq∣∣ 这一项就更明显了,就是两个横坐标的差的绝对值吗,比如还拿 γ ( 1 , 1 ) \gamma(1,1) γ(1,1) 举例,他这项,就是|1-1|=0。
求和,就是把表里面的16个格子都按照公式算一遍,计算过程看figure3。
经过详细的计算:我们算出工资=4!(好低啊,赚了赚了)看来我是一个精明的老板,懂得如何克扣下属哈哈哈。
我惊奇的发现,对角线上的工资,是不用发的!高兴,因为这堆砖头啊,xp=xq相当于本来就在这里,所以小王不费一点力气,就看了他们一眼,他们就算搬过去了咯。这我当然不能发工资了!
所以,按照目前的这个 γ \gamma γ 表格,我们的工资已经算出来了。当然,我是一个聪明的老板,还有些不太聪明的老板。他们的策略可能是这样的!
4
这个老板就显然有点不太聪明的样子了。他让员工把原来都不需要动的砖头搬到了别的地方去。最终造成了劳动力的浪费,我们算出来最后他要发10块钱工资!他完成这个任务付出了我2.5倍的资金。。。
还有很多其他老板,他们也有不同的搬砖策略 γ 1 \gamma1 γ1 γ 2 \gamma2 γ2 γ 3 \gamma3 γ3 …要发不同的工资 B ( γ 1 ) B(\gamma1) B(γ1) B ( γ 2 ) B(\gamma2) B(γ2) B ( γ 3 ) B(\gamma3) B(γ3) …
(3)Wasserstein距离(EM距离)
所谓的EM距离,我们可以理解为诸多老板中,最聪明老板想出的搬砖策略对应的工资。
W ( P , Q ) = m i n γ ϵ Π B ( γ ) ( 公 式 2 ) W(P,Q)=min_{\gamma\epsilon\Pi}{B(\gamma)} \quad (公式2) W(P,Q)=minγϵΠB(γ)(公式2)
这里的这个 Π \Pi Π 就是指所有的老板想出来的所有的搬砖策略 γ 1 \gamma1 γ1 γ 2 \gamma2 γ2 γ 3 \gamma3 γ3 …这些策略构成的集合就是 Π \Pi Π ,而Wasserstein距离,就是从这些策略里面找到工资最少的那个策略对应的工资,如果拿上面的figure2来举例 ,那么很可能,这个W(P,Q)就是4。我就觉得我是最聪明的老板略略略。
2.把Wasserstein距离普遍化
(1)公式的解释
听我扯了这么多搬砖的理论,你一定累了,感觉我这个人太low,太粗俗。好了,我们来看看wgan这个论文里面,作者写的Wasserstein距离的公式是什么吧!
W ( P , Q ) = i n f γ ϵ Π ( P , Q ) E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] ( 公 式 3 ) W(P,Q)=inf_{\gamma\epsilon\Pi(P,Q)}{E_{(x,y)\sim\gamma}[||x-y||]}\quad (公式3) W(P,Q)=infγϵΠ(P,Q)E(x,y)∼γ[∣∣x−y∣∣](公式3)
看着这么复杂的公式。我也犯怵,来让我们一起看看他是啥意思。inf是取下界的意思。
5
看上图的文字, γ \gamma γ仍然是指一个策略,比如搬砖,就是那个表格。而其他情况,分布是很复杂的,这个策略并不是一个表格这么简单。而 Π ( P , Q ) \Pi(P,Q) Π(P,Q) 还是指把P转换成Q的所有策略,还是可以理解为所有的搬砖方法,即所有的 γ \gamma γ 。
现在这个 γ \gamma γ 复杂一点可以叫做,联合分布,简单一点就是我们上面说的那个表格。后面的期望是什么意思呢?
我们知道,期望分为连续型分布的期望,和离散型分布的期望,看上图,我已经写了出来该怎么去求这个期望。对于连续就是求二重积分,离散就是二重求和。
多说无益,我来举个例子,就拿离散型的二维联合分布来举例子吧!看看用论文里的公式该怎么求这个Wasserstein距离!
(2)对某个离散型联合分布gamma的期望计算
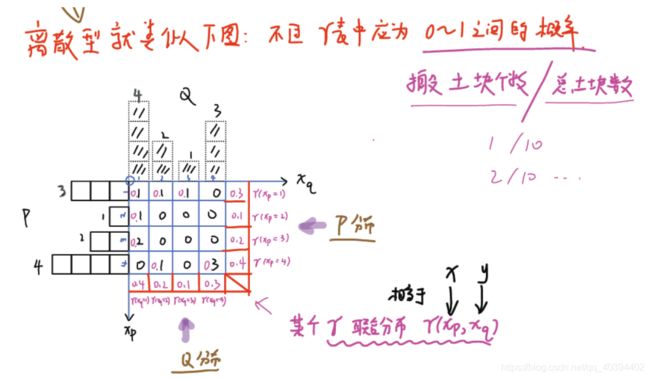
我把figure4那个不太聪明的老板的策略引来了,他现在就是策略 γ \gamma γ 也可以叫做联合分布 γ \gamma γ。
既然是联合分布,那么联合分布里面的数值就应该是概率。那么怎么把搬砖数改成概率呢?这好说,总共有10块砖,那么概率就是砖块数目/10。
所以,我们那个不太聪明的老板的搬砖策略就变成了一个二维联合分布 γ ( x p , x q ) \gamma(x_p,x_q) γ(xp,xq) 。有两个变量,分别是 x p , x q x_p,x_q xp,xq ,你就把他们当成概率论书上写的x,y就行了。
表格里的转块数全部除以10 ,填到表里面。现在,这个表就变成了一个完美的二维离散型联合分布了。我们把两边再补上两列,如figure6红色的线所示,每一行加起来,刚好就是P对应位置的砖头数目/10;每一列加起来,刚好就是Q对应位置的砖头数目/10。(等等,这个结论好像似曾相识哎)。我们再想一下,这不就是概率论里面讲的边缘分布吗!再看看,不就是P和Q的分布吗!
所以就是说,每一个联合分布 γ \gamma γ 的边缘分布都是P和Q。无论你的联合分布长成什么样子,它的边缘分布一定是P和Q。
好了,按照论文里的公式,我可以算一下这个联合分布 γ \gamma γ 他的期望咯,算出来是1.0。
回去看一眼figure4,不太聪明的老板他的工资是10,这个期望就是10/砖头总数10=1.0。
E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] {E_{(x,y)\sim\gamma}[||x-y||]} E(x,y)∼γ[∣∣x−y∣∣]
依次类推,我这个聪明的老板,归纳出的联合分布的期望应该是4/10=0.4吧!
(3)Wasserstein公式到底算出的是什么
刚才我举例的 γ \gamma γ是那个不太聪明的老板提出的一个二维联合分布是吧。别忘了,我还是一个贪心的聪明老板呢!按我的方法,期望是0.4啊!比1要小很多。当然还有很多老板提出了很多二维联合分布啊 γ 1 , γ 2 , γ 3.... \gamma1,\gamma2,\gamma3.... γ1,γ2,γ3.... 他们都能算出一个期望来。我还是觉得,我的期望最小了,那么把这么些个 γ 1 , γ 2 , γ 3.... \gamma1,\gamma2,\gamma3.... γ1,γ2,γ3.... 他们的期望都算一算,从里面挑出一个最好的 γ \gamma γ ,它对应的期望,就是Wasserstein距离!
我可以很自信的告诉你,这个例子里,Wasserstein距离就是 0.4!没错,就是我的这个二维联合分布对应的期望啦啦。
3.总结
综上所述,Wasserstein距离其实就是:把一个分布P变换到另一个分布Q,这么多种联合分布( γ 1 , γ 2 , γ 3.... \gamma1,\gamma2,\gamma3.... γ1,γ2,γ3....)里面,可以使
E ( x , y ) ∼ γ [ ∣ ∣ x − y ∣ ∣ ] {E_{(x,y)\sim\gamma}[||x-y||]} E(x,y)∼γ[∣∣x−y∣∣],最小的那个期望值。
我bb完了,懂得都懂。
注解
P和Q的分布示意图。 ↩︎
搬砖示意图,图中的一些文字我会在下面的“算账中进行解释” ↩︎
工资计算过程 ↩︎
不太聪明的老板的搬砖策略 ↩︎
解释书面版本的Wasserstain距离 ↩︎
解释离散型联合分布的EM距离求法 ↩︎
按照面公式计算一个二维离散联合分布的Wasserstain距离 ↩︎