用Python实现DT算法

目录

一、前言

二、示例数据

三、DT法分级步骤

四、Python实现

五、结果

---

一、前言

DT法是由我国学者林韵梅于 1988 年提出的,首先应用于围岩稳定性动态分级的一种方法。该方法的核心思想来源于多元统计分析中的动态聚类法，是根据“物以类聚”的道理，对样本或指标进行分类。动态聚类的基本思路是，所有样本应被划分到与之最接近的类别当中。首先根据样本的基础特性给出多个凝聚点，即欲形成“类”的中心，计算各样本到凝聚点的距离，将样本划入最近的凝聚点，形成一个粗糙的初始分类，然后按照一定的原则，调整初始分类，直到分类合理时，输出分类结果。在调整分类的过程中就是样本间的距离误差被不断修正，当误差达到可接受的范围，即可得到相对准确的结果。在反复修改过程中，样本的级别允许动态调整，可以与初始分级有所变化，这和静态分级方法中，样本一旦划入某个类以后就不再改变的处理方法有明显的不同。

二、示例数据

矿岩名称	抗压强度Rc（MPa）	容重ρ（g/cm3）	完整系数	炸药单耗q（kg/m3）
阳起石英岩	226.76	2.94	0.18	0.88
细粒斜长角闪岩	153.6	3.03	0.2	0.76
花岗岩	106.05	2.69	0.21	0.59
伟晶岩	95.46	2.69	0.19	0.59
辉绿岩	69.58	3.01	0.15	0.6
绿泥角闪岩	78.17	2.97	0.38	0.77
赤铁磁铁石英岩	144.26	3.37	0.37	0.74
磁铁石英岩	129.86	3.42	0.36	0.82
第六层铁矿	250.4	3.48	0.2	1.08
第五层铁矿	193.56	3.42	0.23	0.96
第二层铁矿	186.05	3.49	0.29	0.98
第三层铁矿	168.78	3.41	0.15	0.89
赤铁石英岩	205.5	3.38	0.89	0.7
石英岩	200.4	2.69	0.95	0.6
绿泥岩	39	2.93	0.94	0.3
混合岩	68.6	2.58	0.91	0.5
赤铁石英岩	192.71	3.48	0.38	0.63
底盘角闪岩2	60.4	2.88	0.39	0.75
矽石山石英岩	160.68	2.63	0.34	0.74

三、DT法分级步骤

来源：基于DT法的石油化工码头储罐区危险源动态分级研究_崔益源[D]

 

四、Python实现

import pandas as pd
import numpy as np
from numpy import *
import sympy as sp

import matplotlib.pyplot as plt
import numpy as np
from sympy import *
import math

from pylab import *
plt.rcParams['axes.unicode_minus']=False  #用于解决不能显示负号的问题
mpl.rcParams['font.sans-serif'] = ['SimHei']

data =  pd.read_excel("DT分析样本.xlsx",index_col="矿岩名称")  
S = np.sqrt(((data-data.mean())**2).sum()/(len(data.index)-1))
x2_2 = (data - data.mean())/S
S_i = x2_2.sum(axis=1)
AMAX = max(S_i)
AMIN = min(S_i)
K = 19

NC_i = np.floor(((K-1)*(AMAX-S_i)/(AMAX-AMIN))+0.5)+1
NC_i = pd.DataFrame(NC_i)
NC_i.columns = ["NC"]
data = data.add(NC_i,fill_value=0)

x = []
y = []
for K in range(2,20):
    data =  pd.read_excel("DT分析样本.xlsx",index_col="矿岩名称")  
    S = np.sqrt(((data-data.mean())**2).sum()/len(data.index))
    x2_2 = (data - data.mean())/S
    data = (data - data.mean())/S
    S_i = x2_2.sum(axis=1)
    AMAX = max(S_i)
    AMIN = min(S_i)

    NC_i = np.floor(((K-1)*(AMAX-S_i)/(AMAX-AMIN))+0.5)+1
    NC_i = pd.DataFrame(NC_i)
    NC_i.columns = ["NC"]
    data = data.add(NC_i,fill_value=0)

    for i in range(300):
#         print(K,i)
        temp = data["NC"].copy()

        value = pd.DataFrame(columns=["type","num","value"])
        for eachIndex in data.index:
            for each in set(data["NC"]):
                value = value.append({"type":eachIndex,"num":each,"value":np.sqrt(((data.loc[eachIndex] - data[data["NC"] ==each].mean())**2).sum())},ignore_index=True)
        value = value.set_index(["type"])
        for index in set(value.index):
            data.loc[index]["NC"] = value.loc[index].sort_values("value").iloc[0]["num"]


        if (temp-data["NC"]).abs().sum() < 0.001:
            sum = 0
            for index in data.index:
                sum += value.loc[index][value.loc[index]["num"]==data.loc[index]["NC"]]["value"].sum()
            x.append(K)
            y.append(sum)
            print(K,sum)
            break

  PS：在线多项式拟合网站 

plt.figure(figsize=(8,4))

x_1 = np.linspace(2,19,500)
y_1 = 33.1714313933564 - 2.6804554847376*x_1 + 0.0626813808370871*x_1**2 + 0.00359821535505567*x_1**3 - 0.00018026487545368*x_1**4

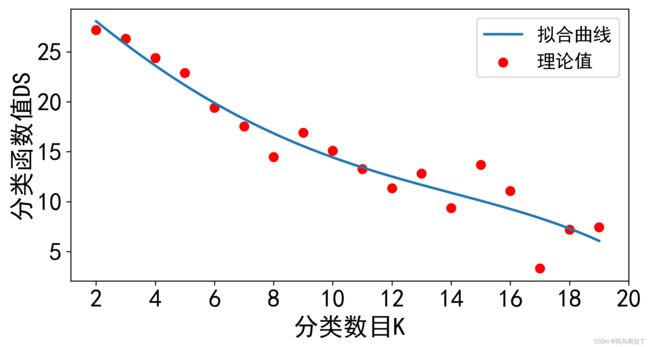
plt.scatter(x,y,label="理论值",linewidth=2,color="r")
plt.plot(x_1,y_1,linewidth=2,label="拟合曲线")
plt.xlabel("分类数目K",fontsize=20)
plt.ylabel("分类函数值DS",fontsize=20)
plt.yticks([5,10,15,20,25])
plt.xticks([2,4,6,8,10,12,14,16,18,20])

plt.legend(fontsize=15)
plt.tick_params(labelsize=20)
plt.savefig("DS",dpi=300,bbox_inches ="tight")

五、结果