torch.nn模块之卷积层详解
torch中的卷积层
- 1. torch.nn模块中的卷积层简介
- 2. 卷积运算特点
- 3. 卷积的调用方式
- 4. 图像卷积演示
- 参考资料
1. torch.nn模块中的卷积层简介
t o r c h . n n torch.nn torch.nn模块包含着t o r c h orch orch已经准备好的卷积层,方便使用者调用构建网络。卷积可以看作是输入和卷积核之间的内积运算,是两个实值函数之间的一种数学运算。在卷积运算中,通常使用卷积核将输入数据进行卷积运算得到输出作为特征映射,每个卷积核可获得一个特征映射。
例如,二维图像卷积运算过程示意图如下图1所示。卷积核大小为2×2,步长为1。
2. 卷积运算特点
使用卷积运算在图像识别、图像分割、图像重建等应用中有三个好处:
- 稀疏连接: 在卷积神经网络中,通过输入卷积核来进行卷积操作,使输入单元(图像或特征映射)和输出单元(特征映射)之间的连接是稀疏的,这样能够减少需要训练参数的数量,从而加快网络的计算速度。
- 参数共享: 模型中同一组参数可以被多个函数或操作共同使用。
- 等变表示: 由于卷积核尺寸可以远远小于输入尺寸,即减少需要学习的参数的数量,并且针对每个卷积层可以使用多个卷积核获取输入的特征映射,对数据具有很强的特征提取和表示能力,并且在卷积运算之后,使得卷积神经网络结构对输入的图像具有平移不变的性质。
3. 卷积的调用方式
在PyTorch中针对卷积操作的对象和使用场景的不同,有一维卷积、二维卷积、三维卷积与转置卷积(卷积的逆操作),它们的使用方法比较相似,都从torch.nn模块中调用,常用的卷积操作对应的类有torch.nn.Conv1d()、torch.nn.Conv2d()、torch.nn.Conv3d()、torch.nn.ConvTranspose1d()、torch.nn.ConvTranspose2d()、torch.nn.ConvTranspose3d()。
以torch.nn.Conv2d()为例,其调用方式为:
torch.nn.Conv2d(in_channels,
out_channels,
kernel_size,
stride=0,
padding=1,
dilation=1,
groups=1,
bias=True)
| 卷积参数 | 说明 |
|---|---|
| in_channels | 输入图像的通道数(整数) |
| out_channels | 经过卷积运算后,输出特征映射的数量(整数) |
| kernel_size | 卷积核的大小(整数或者数组) |
| stride | 卷积的步长(整数或者数组,正数),默认为1 |
| padding | 在输入两边进行0填充的数量(整数或者数组,正数),默认为0 |
| dilation | 卷积核元素之间的步幅(整数或者数组,正数),可调整空洞卷积的空洞大小,默认为1 |
| groups | 从输入通道到输出通道的阻塞连接数(整数,正数) |
| bias | 是否添加偏置(布尔值)默认为True |
torch.nn.Conv2d()输入的张量为 ( N , C i n , H i n , W i n ) (N,C_{in},H_{in},W_{in}) (N,Cin,Hin,Win),输出张量为 ( N , C o u t , H o u t , W o u t ) (N,C_{out},H_{out},W_{out}) (N,Cout,Hout,Wout)。
其中,
H o u t = [ H i n + 2 × p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] × ( k e r n e l s i z e [ 0 ] − 1 ) − 1 s t r i d e [ 0 ] ] H_{out}=[\frac{H_{in}+2×padding[0]-dilation[0]×(kernel size[0]-1)-1}{stride[0]}] Hout=[stride[0]Hin+2×padding[0]−dilation[0]×(kernelsize[0]−1)−1]
W o u t = [ W i n + 2 × p a d d i n g [ 1 ] − d i l a t i o n [ 1 ] × ( k e r n e l s i z e [ 1 ] − 1 ) − 1 s t r i d e [ 1 ] ] W_{out}=[\frac{W_{in}+2×padding[1]-dilation[1]×(kernel size[1]-1)-1}{stride[1]}] Wout=[stride[1]Win+2×padding[1]−dilation[1]×(kernelsize[1]−1)−1]
4. 图像卷积演示
下面使用一张图像来展示经过卷积后,输出的特征映射结果。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
#读取图像
img = Image.open('lena.jpg')
#转化为灰度图像->转化为numpy数组
img_gray = np.array(img.convert('L'), dtype=np.float32)
# 可视化图片
plt.figure(figsize=(12, 6))
plt.subplot(121), plt.imshow(img, cmap=plt.cm.gray)
plt.axis('off')
plt.subplot(122), plt.imshow(img_gray, cmap=plt.cm.gray)
plt.axis('off')
plt.show()
imh, imw = img_gray.shape
# 将numpy数组转化为张量
img_gray_t = torch.from_numpy(img_gray.reshape((1, 1, imh, imw)))
print(img_gray_t.shape)
#卷积时 需将 图像转化为四维来表示 [batch,channel,h,w]
'''
在对图像进行卷积操作后,获得两个特征映射:
1、使用图像轮廓提取卷积核获取
2、第二个特征映射使用的卷积核为随机数,卷积核大小为5x5,对图像的边缘不使用0填充,所以卷积后输出的特征映射的尺寸为508x508
'''
#对灰度图像进行卷积提取图像轮廓
kersize=5 #定义边缘检测卷积核,并将维度处理为1*1*5*5
ker = torch.ones(kersize, kersize, dtype=torch.float32)*-1
ker[2, 2] = 24
ker = ker.reshape(1, 1, kersize, kersize)
print("边缘检测核:", ker)
# 进行卷积操作
conv2d = nn.Conv2d(1, 2, (kersize, kersize), bias=False)
# 设置卷积时使用的核,第一个卷积核使用边缘检测
conv2d.weight.data[0] = ker
# 对灰度图像进行卷积操作
imconv2out = conv2d(img_gray_t)
# 对卷积后的输出进行维度压缩
imconv2dout_im = imconv2out.data.squeeze()
print("卷积后尺寸:", imconv2dout_im.shape)
# 可视化卷积后的图像
plt.figure(figsize=(12, 6))
plt.subplot(121), plt.imshow(imconv2dout_im[0], cmap=plt.cm.gray)
# print(imconv2dout_im[0])
plt.axis("off")
plt.subplot(122), plt.imshow(imconv2dout_im[1], cmap=plt.cm.gray)
print("随机卷积核:", conv2d.weight.data[1])
plt.axis("off")
plt.show()
>>>torch.Size([1, 1, 512, 512])
>>>边缘检测核: tensor([[[[-1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1.],
[-1., -1., 24., -1., -1.],
[-1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1.]]]])
>>>卷积后尺寸: torch.Size([2, 508, 508])
>>>随机卷积核: tensor([[[ 0.1073, -0.0845, 0.1682, -0.0216, 0.1601],
[-0.0093, 0.0872, -0.1010, 0.0225, 0.1679],
[ 0.1727, -0.1691, 0.1962, 0.0538, -0.0414],
[ 0.0753, 0.0023, 0.0936, 0.0997, 0.1308],
[ 0.1836, -0.0755, 0.1368, -0.1681, 0.1361]]])
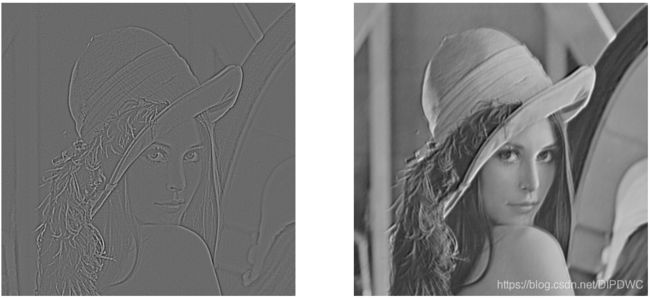
从图3中可以看出,使用边缘特征提取卷积核较好的提取除了图像的边缘信息,右边的图像使用的卷积核为随机数,得到的卷积结果与原始图像较相似。
参考资料
- 《PyTorch 深度学习入门与实战(案例视频精讲)》,孙玉林,余本国著. 北京:中国水利水电出版社,2020.7
![]()