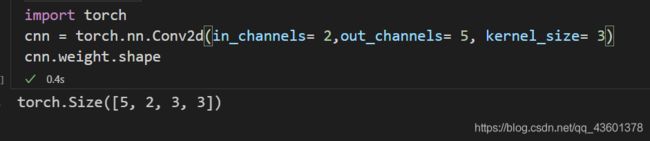
清晰图解，一图看懂图卷积GCN、时空图卷积ST-GCN

1.前言

本文为我阅读论文 Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition 和代码后的所思所想，仅代表我个人观点

2.普通卷积与图卷积

2.1 普通卷积

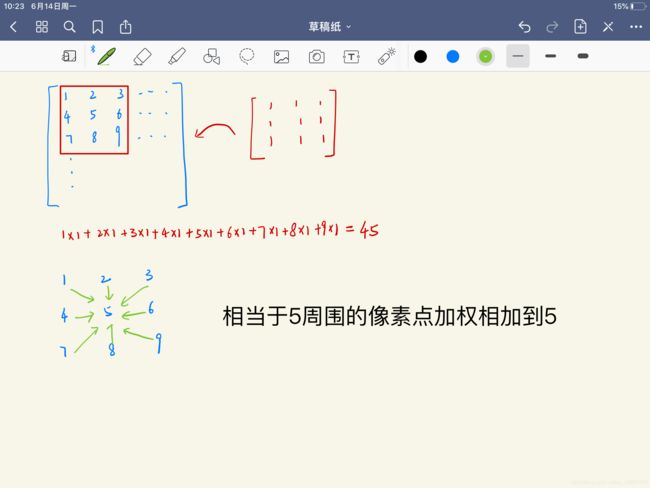
在理解图卷积之前，需要认识一下传统的卷积。对于一个3×3的卷积操作而言，相当于把3×3的卷积核在图像上滑动。每一次会有对应的9个数字相乘之后相加，然后得到一个最终的值。
在这里，换一个角度来看，图像上的每一个数字都是一个特征，而卷积的操作，是以一个像素点为中心，将其周围的8个点连同它自己的特征加权（卷积核的值）后加到一起，更通俗地理解为：将一个点的特征变为它周围所有邻居的特征的加权和。下图中卷积核参数全为1，相当于加权值为1。

2.2 图卷积

对于一个图结构而言，我们可以通俗易懂地把图卷积理解为把一个节点邻居节点的特征加权并相加到该节点，当然，一个节点可能有许多的特征向量，我们会在之后说明这一点。

请记住上面这个简单的图，我们会以该图为例子进行展开。在这个简单的图结构中，我们要进行图卷积，可以这样理解：对于节点2而言，我们需要提取1和3的特征添加到2中去，怎么样选择邻接节点是图卷积的重点。
由于在图片中，像素点紧密连接，天然存在一个遍历序列，如对于一个3×3的卷积而言，我们可以通过两次0-1-2的for循环遍历到这9个像素点。但对于图而言，没有天然存在的顺序用于遍历。因此，为了能遍历邻居节点，我们需要构建邻接矩阵。对于一个庞大的图结构而言，不可能把所有的节点特征直接相加，为了划分图结构中的邻居节点，ST-GCN中提出将每个邻居节点编一个序号，同一个序号的邻居节点看做一个邻居子集，也就形成了多个邻接矩阵，文中提出了三种分区策略：

1. 简单分区：所有节点都为一个索引，上图( b )，绿色全部为同一组节点；
2. 距离分区：通过不同距离，将一个图（如人体骨骼）按照与目标节点的距离分为几部分，上图( c ），绿色是距离为0的节点，也就是节点本身，蓝色是距离为1的邻居节点，也就是与其直接相连的节点；
3. 空间配置分区：通过对于目标节点而言近心端和远心端的节点进行分区，上图( d )，绿色是节点本身，蓝色是比原节点更接近重心的邻居节点集，黄色是远离重心的邻居节点集。

在本文中，我们仅讨论距离分区。

对于之前提到的 1-2-3 的简单图结构，我们画出其距离为0和距离为1的邻接矩阵：

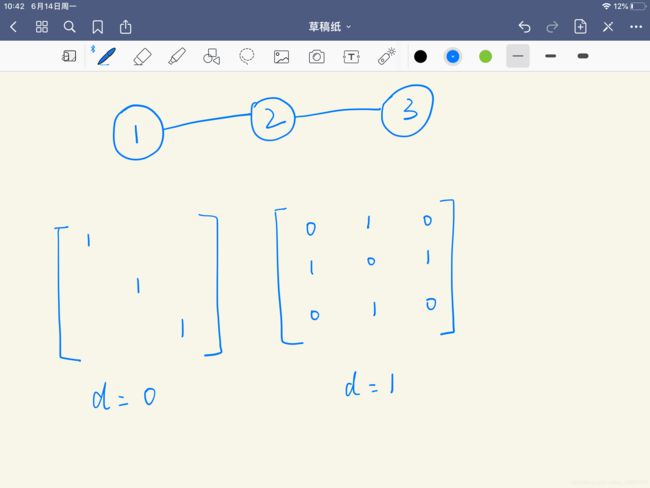
距离为0即为节点自己本身，距离为1即与他相连的邻居节点。

假设经过特征提取后，每一个节点都包括60个特征，即对于上述图结构，特征向量矩阵为60×3，对于距离为1的邻接矩阵而言，其维度为3×3，两个矩阵做点乘得到60×3的矩阵，其过程如下：
假设这三个节点的第一个特征为A,B,C，那么其与距离为1的邻接矩阵相乘后，会得到的第一个维度的特征为B,A+C,B，其余59个特征向量都是如此，我们似乎确实通过邻接矩阵将邻居节点的特征加到了一起。但值得注意的是，因为我们乘的是距离为1的邻接矩阵，这里没有包括节点本身的特征。对于两个分区子集而言，我们分别乘上距离为0和距离为1的邻接矩阵，就能得到60×3×2的特征向量，或者我们将距离为1的邻接矩阵矩阵加上距离为0的邻接矩阵，再乘上特征矩阵，可以得到包括自身的特征和，如下图所示。

为了平衡每一个节点的贡献，ST-GCN中提出了一个正则化的邻接矩阵，其过程如下：对于每一个邻接矩阵而言，我们创建一个对角矩阵$\Lambda$，它的每一行的值为该节点邻居节点数量的倒数，然后将之前的邻接矩阵与$\Lambda$点乘，得到正则化的邻接矩阵，通过该邻接矩阵，我们再用之前的特征矩阵相乘，会发现节点之间的权重被平均，如下图所示。

3 ST-GCN图卷积的代码解读

有了以上的理论基础，解读ST-GCN的代码就简单得多了
以下代码在人体骨架上实现，如下图：

对于邻接矩阵的定义，主要分三块：获取边，得到邻接矩阵，对邻接矩阵进行正则化

class Graph():
    def __init__(self, max_hop=1, dilation=1):
        self.max_hop = max_hop
        self.dilation = dilation

        # get edges 获取边
        self.num_node, self.edge, self.center = self._get_edge() #节点，边，中心脊柱
        
        # get adjacency matrix 获取邻接矩阵
        self.hop_dis = self._get_hop_distance() #得到距离矩阵
        
        # normalization 正则化
        self.A = self._get_adjacency()

    def __str__(self):
        return self.A

    def _get_edge(self):
        num_node = 25 #人体骨架节点数
        neighbor_1base = [(1, 2), (2, 21), (3, 21), (4, 3), (5, 21),
                          (6, 5), (7, 6), (8, 7), (9, 21), (10, 9),
                          (11, 10), (12, 11), (13, 1), (14, 13), (15, 14),
                          (16, 15), (17, 1), (18, 17), (19, 18), (20, 19),
                          (22, 23), (23, 8), (24, 25), (25, 12)] #所有相连的节点
        self_link = [(i, i) for i in range(num_node)] #自己与自己相连的元组
        neighbor_link = [(i - 1, j - 1) for (i, j) in neighbor_1base] #序号从1开始，故需要 -1，所有相连的元组
        edge = self_link + neighbor_link #所有相连的元组
        center = 21 - 1 #中心脊柱是21
        return (num_node, edge, center)

    def _get_hop_distance(self):
        A = np.zeros((self.num_node, self.num_node))
        for i, j in self.edge: #相连的为1
            A[j, i] = 1
            A[i, j] = 1
        hop_dis = np.zeros((self.num_node, self.num_node)) + np.inf #25*25的矩阵，值为无限大（代表距离）
        transfer_mat = [np.linalg.matrix_power(A, d) for d in range(self.max_hop + 1)] #得到（最大距离+1，25,25）的转移矩阵，
        #即距离为0以内的矩阵（单位矩阵，自己和自己相连），距离为1以内的矩阵。。。以此类推
        #np.linalg.matrix_power()表示矩阵的次方
        arrive_mat = (np.stack(transfer_mat) > 0) #将转移矩阵值变为True和False
        for d in range(self.max_hop, -1, -1): #从最大距离开始到0，，如2,1,0
            hop_dis[arrive_mat[d]] = d  #通过矩阵从距离远到近进行覆盖，实现一个25*25矩阵里的值为两个节点的最近距离，无法到达为inf
        return hop_dis

    def _get_adjacency(self):
        valid_hop = range(0, self.max_hop + 1, self.dilation)
        adjacency = np.zeros((self.num_node, self.num_node))
        for hop in valid_hop:
            adjacency[self.hop_dis == hop] = 1  #所有相连的节点（包括在能到达的节点）都为1
        normalize_adjacency = self._normalize_digraph(adjacency)
        A = np.zeros((len(valid_hop), self.num_node, self.num_node))
        for i, hop in enumerate(valid_hop): #对于不同距离的邻接矩阵进行正则化
            A[i][self.hop_dis == hop] = normalize_adjacency[self.hop_dis == hop]
        return A

    def _normalize_digraph(self, A):
        Dl = np.sum(A, 0) #每个节点相连的个数
        num_node = A.shape[0]
        Dn = np.zeros((num_node, num_node))
        for i in range(num_node):
            if Dl[i] > 0:
                Dn[i, i] = Dl[i]**(-1) #值为当前节点连接节点数的倒数
        AD = np.dot(A, Dn) #修改邻接矩阵
        return AD

构建完邻接矩阵后，进行图卷积的代码如下：

class SpatialGraphConv(nn.Module):
    def __init__(self, in_channels, out_channels, s_kernel_size):
        super().__init__()

        # spatial class number (distance = 0 for class 0, distance = 1 for class 1, ...)
        self.s_kernel_size = s_kernel_size #最大距离+1

        # weights of different spatial classes
        self.conv = nn.Conv2d(in_channels, out_channels * s_kernel_size, kernel_size=1)

    def forward(self, x, A):

        # numbers in same class have same weight
        x = self.conv(x)    #x维度(batch_size,192,300,25),意思为 batch_size，64*3（通道*最大距离+1）,300帧，25个节点

        # divide into different classes
        n, kc, t, v = x.shape  #batch_size,通道*（最大距离+1），帧数，节点个数
        x = x.view(n, self.s_kernel_size, kc//self.s_kernel_size, t, v) #batch_size,最大距离+1，通道数，帧数，节点数
        #x维度(batch_size,3,64,300,25),A维度(3,25,25)
        # spatial graph convolution
        x = torch.einsum('nkctv,kvw->nctw', (x, A[:self.s_kernel_size])).contiguous() #简化的矩阵点乘，对k，v求和
        #这里相当于每个节点有64*300个特征，然后共有25个节点，64*300*25的矩阵乘上25*25的邻接矩阵，得到64*300*25的矩阵，共3个不同距离的邻接矩阵，得到3*64*300*25的结果，演着邻接矩阵个数的方向想加，得到最终结果64*300*25的矩阵。
        #得到batch,通道，帧数，节点数
        #x维度（batch_size,64,300,25)
        return x

每一段代码我都尽可能做了注释，便于理解。

4.图卷积的缺陷

不知道大家在使用CNN时有没有发现一个问题：卷积操作相当于把一个卷积核在一张平面图上拖动，但是，我们使用的RGB图片共三维，也就是三个通道。对于三个通道而言，二维的卷积核是怎么拖动的？对于这个问题，我最开始认为卷积核会以R、G、B的顺序依次遍历三个通道，然后对应位置相加。这个说法对，但没有完全对，卷积核确实是这么干的，但它在每一个通道上都有不同的参数，相当于在每一个通道上有一个新的卷积核。我们举个例子：

在这堆代码中，我们定义了一个5个卷积核，每一个卷积核为3×3大小，输入维度假设为2（本来图片是3个维度，为了与卷积核的维度区分开这里设为2）。如果每一个卷积核真的是依次遍历2个输入维度的话，那么只需要5×3×3个参数即可完成遍历，但当我们输出维度，却发现多了一个2，这说明，卷积核在每一个输入维度都有不同的参数。

如下图所示（来源参考文献[3]），CNN在每一个输入维度上都有不同的参数，相当于有不同的卷积核（也被称为聚集核），这种现象在部分论文中被称为解耦合聚集。$X$代表输入特征，$C$表示输入通道，如上文的RGB通道等，$C^{{}^{\prime }}$表示输出通道数，即卷积核个数，不同的颜色代表不同的卷积核。

而对于GCN而言，聪明的你也许以及发现，对于不同的输入通道而言，邻接矩阵（相当于卷积核）永远都是一样的，如下图所示（来源参考文献[3]）。这种现象在一些论文中被称为耦合聚集。

尽管有部分论文提出邻接矩阵可以训练来获得灵活性，但它仅仅是在训练中每一个epoch不同。对于一个具体的epoch而言，邻接矩阵对于不同维度的特征还是一样的。因此，参考文献[3]便以GCN的解耦合为创新点进行了实验，取得了比较好的效果，如下图所示。大家有兴趣可以自行翻阅。

5 参考文献

参考文献：
[1] Yan S , Xiong Y , Lin D . Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition[J]. 2018.

[2] Song Y F , Zhang Z , Shan C , et al. Richly Activated Graph Convolutional Network for Robust Skeleton-based Action Recognition[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2020, PP(99):1-1.

[3] Cheng, K., et al. (2020). Decoupling gcn with dropgraph module for skeleton-based action recognition. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XXIV 16, Springer

6 联系方式

同为初学者，难免会遇到错误，如有错误欢迎在评论区指出，有问题也可以通过以下方式联系，看到必回（没看到另说(*￣︶￣)）：

QQ邮箱：[email protected]
163邮箱：[email protected]