线索二叉树与Morris遍历
一、二叉树线索化
对于一棵普通的二叉树，它的节点结构需要由两个指针域和一个数据域构成。而一棵树中必定存在一些指针域没有被使用到，这就造成了空间的浪费。
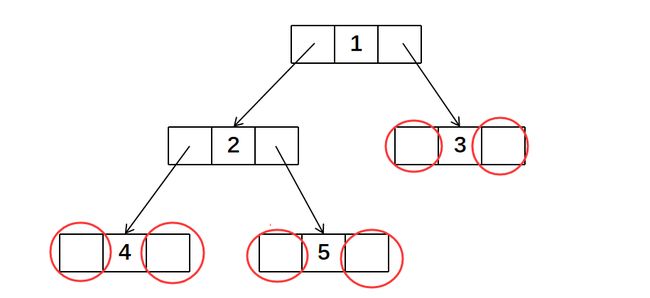
另一方面，我们经常用到二叉树的前、中、后序遍历，如果想求某种遍历中某个节点的前驱和后继节点，那就需要重新进行遍历。这无疑会造成时间的浪费。
所以为什么不把空闲的指针域利用起来，让其指向节点的前驱或后继呢？其实这就是线索二叉树的核心思想。
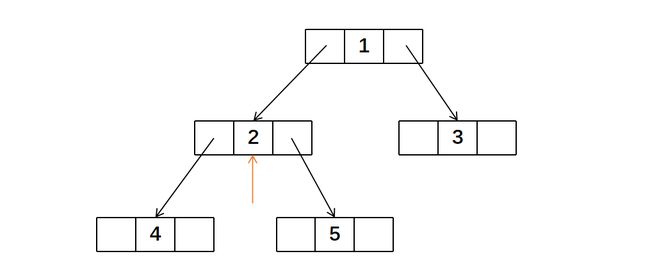
我们以中序遍历为例进行讲解。对于前面那棵二叉树，我们很容易得出它的中序遍历结果为：42513。但对于计算机来说，它只知道当前遍历到的节点cur，以及我们可以缓存下来的前一个遍历到的节点pre。
于是，计算机首先遍历到「4」这个节点
显然，这个节点的左右指针是空的，这两个指针域可以利用起来。但这个节点并没有前驱节点，而后继节点计算机并不知道是谁，所以这两个指针域还是只能指向空。
接下来遍历到「2」这个节点
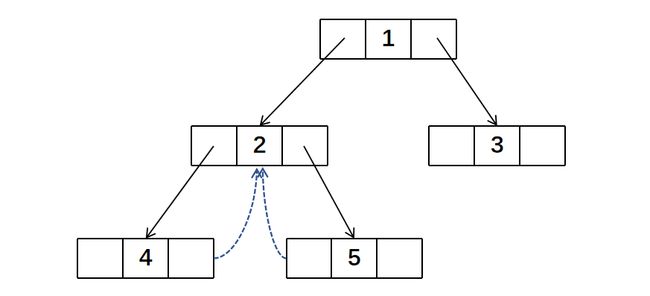
虽然「2」节点的左右指针都不是空的，但它的前驱节点「4」的右指针还没有指向后继节点。而「4」的后继节点正是「2」节点。所以我们将「4」的右指针指向「2」
接下来指针遍历到了「5」节点
此时「5」节点的左指针为空，而且它的前驱我们知道是「2」，所以将左指针指向「2」
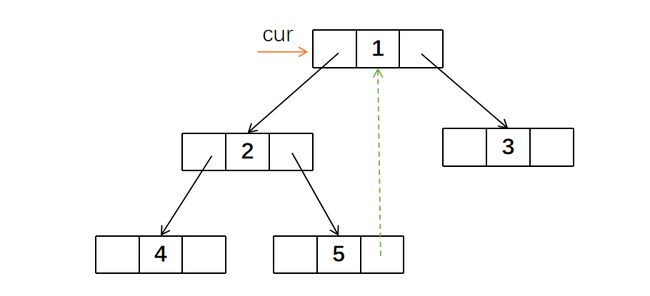
接下来指针遍历到「1」节点，它的前驱节点「5」的右指针为空，所以将「5」的右指针指向「1」
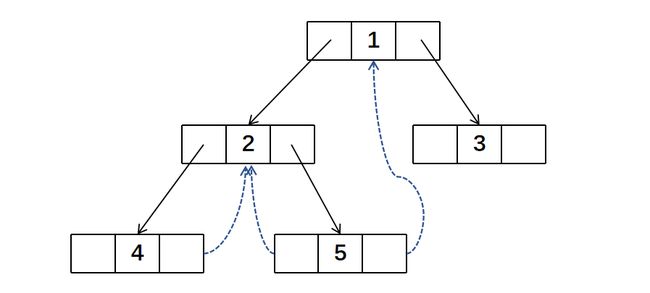
最后，指针遍历到「3」，它的左指针为空，所以将左指针指向「1」
至此，线索二叉树就构建完成了。但对于计算机来说，并不知道哪些指针是指向前驱或后继的指针，哪些指针是指向左右孩子的指针。所以我们还需要在二叉树节点的结构中引入两个bool变量，区分该指针是否是线索。
public class ThreadedBinaryTreeNode<T>
{
public T data;
public ThreadedBinaryTreeNode<T> left;
public ThreadedBinaryTreeNode<T> right;
public bool leftTag;
public bool rightTag;
}
线索化的代码如下：
public void InThreading()
{
InThreadingMethod(Head);
// 处理遍历的最后一个节点
if (_pre != null) _pre.RightTag = true;
}
private ThreadedBinaryTreeNode<T>? _pre;
private void InThreadingMethod(ThreadedBinaryTreeNode<T>? head)
{
if(head == null) return;
InThreadingMethod(head.Left);
// 前驱线索
if (head.Left == null)
{
head.Left = _pre;
head.LeftTag = true;
}
// 后继线索
if (_pre != null && _pre.Right == null)
{
_pre.Right = head;
_pre.RightTag = true;
}
_pre = head;
InThreadingMethod(head.Right);
}
完成线索化后，当我们需要查询某个节点的后继时，如果它有后继指针，那就可以直接返回后继指针指向的节点；否则就返回其右子树按中序遍历的第一个节点（最左节点）
public ThreadedBinaryTreeNode<T>? GetNext(ThreadedBinaryTreeNode<T> node)
{
// 有后继指针,直接返回
if (node.RightTag) return node.Right;
// 否则返回右子树按中序遍历的第一个节点
var root = node.Right;
while (root != null && !root.LeftTag)
{
root = root.Left;
}
return root;
}
当需要查询某个节点的前驱时，如果它有前驱指针，则直接返回前驱指针指向的节点；否则就返回其左子树按中序遍历的最后一个节点（最右节点）
public ThreadedBinaryTreeNode<T>? GetPre(ThreadedBinaryTreeNode<T> node)
{
// 有前驱指针,直接返回
if (node.LeftTag) return node.Left;
// 否则返回左子树按中序遍历的最后一个节点
var root = node.Left;
while (root != null && !root.RightTag)
{
root = root.Right;
}
return root;
}
明白了如何寻找前驱后继，那么中序遍历整棵树也就非常简单了
public void Traverse()
{
// 先找到中序遍历的起始节点
var cur = Head;
while (cur != null && !cur.LeftTag)cur = cur.Left;
// 依次寻找后继节点
while (cur!=null)
{
Console.Write(cur.Data);
cur = GetNext(cur);
}
}
线索二叉树的优点是遍历过程不再需要依靠堆栈，相对来讲速度会快一点，且比较省空间。最主要的一点是寻找任意节点的前驱和后继节点变得容易，不需要从头开始遍历。
二、Morris遍历
Morris遍历是对线索二叉树的一种巧妙的利用。它并不是事先进行线索化，而是一边遍历一边进行线索化。这使它的空间复杂度可以降低到 O ( 1 ) O(1) O(1)级别，时间复杂度为 O ( N ) O(N) O(N)。
Morris遍历的基本原理是利用叶子节点空闲的指针，构成回到上层节点的通路，从而避免使用额外的存储结构实现遍历。
Morris遍历的过程如下：
从根节点开始遍历，假设当前节点为cur
（1）如果cur没有左孩子，则前往cur的右孩子（即cur = cur.right）
（2）如果cur有左孩子，则寻找左子树上的最右节点pre
①如果pre的右孩子为空，则将其右指针指向cur，cur向左移动
②如果pre的右孩子为cur，则将其右指针指向空，cur向右移动
下面通过一个例子来演示Morris遍历的过程
首先，cur位于1节点，存在左孩子，所以要寻找左子树上的最右节点，也就是5。5节点的右孩子为空，所以将其右指针指向cur。然后cur左移来到2的位置。
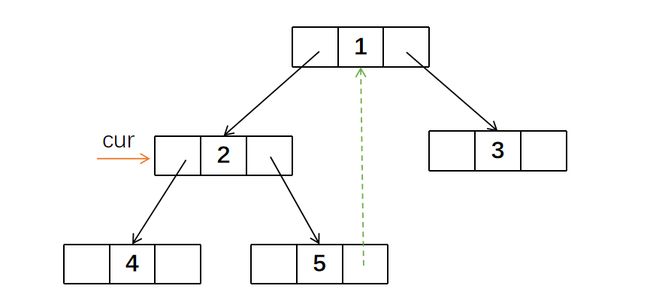
2节点存在左孩子，所以要寻找左子树上的最右节点，也就是4节点。4节点的右孩子为空，所以将其右指针指向cur。cur左移来到4的位置
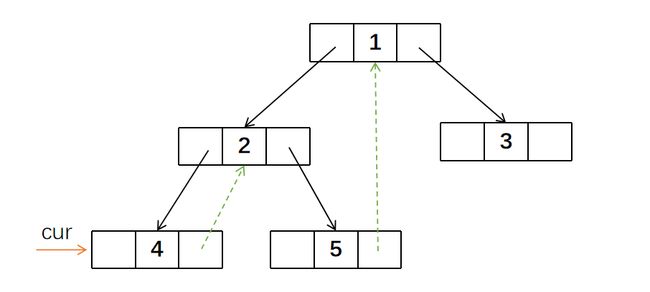
由于4节点没有左孩子，所以cur挪动到右孩子的位置，也就是回到2节点
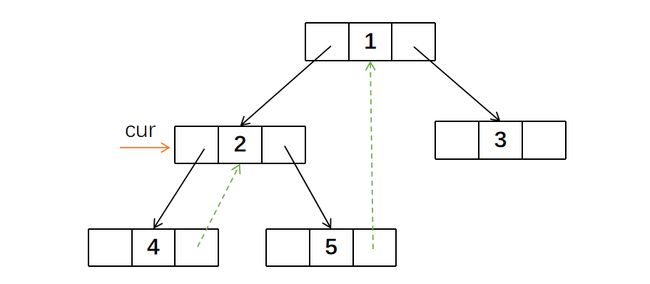
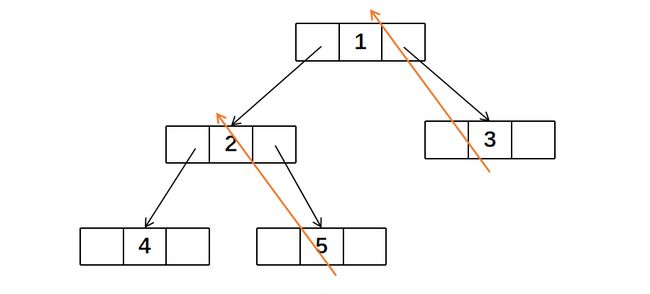
2节点存在左孩子，所以继续寻找左子树的最右节点，也就是4。但4节点的右孩子就是cur，所以将其右指针指向空，然后cur右移来到5节点
5节点没有左孩子，所以cur右移来到1节点。
1节点存在左孩子，所以寻找左子树上的最右节点，也就是5。但5节点的右孩子就是cur，所以将其右指针指向空，cur右移来到3节点
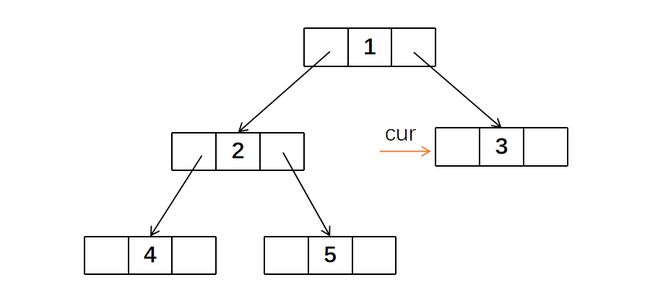
3节点没有左孩子，所以cur右移来到空，遍历结束。
我们将遍历过程中经过的节点一一列出来
1->2->4->(2)->5->(1)->3
可以发现其中一些节点经过了2次。
如果我们将第一次经过视为有效，则遍历结果为12453，正是前序遍历的顺序；
如果将第二次经过视为有效，则遍历结果为42513，正是中序遍历的顺序。
至于后序遍历就有些复杂了。常规的Morris遍历只能保证根节点一定在右节点之前遍历到，而后序遍历则需要先遍历到右节点，再遍历到根。所以只能中序遍历的基础上，将根->右的遍历顺序进行反转，成为右->根。操作方法是，在执行到（2）②步骤，将cur右移之前，先将cur左子树的右边界进行逆转，然后遍历，然后再逆转回来。具体可以参考代码。
前序遍历
// 寻找左子树最右节点
private TreeNode<T> FindMostRightParentInLeftTree<T>(TreeNode<T> head)
{
if (head?.Left == null) throw new NullReferenceException();
TreeNode<T> cur = head.Left;
while (cur != null && cur.Right != null && cur.Right != head)
{
cur = cur.Right;
}
return cur;
}
/// 中序遍历（只是换一下打印的位置）
/// 后序遍历
// 逆序右边界
private TreeNode<T> ReverseRightBorder<T>(TreeNode<T> head)
{
TreeNode<T>? pre = null;
while (head != null)
{
TreeNode<T>? next = head.Right;
head.Right = pre;
pre = head;
head = next;
}
return pre;
}
// 逆序打印右边界
private void ReversePrintRightBorder<T>(TreeNode<T> head)
{
// 反转右边界
var tail = ReverseRightBorder(head);
TreeNode<T> cur = tail;
// 遍历
while (cur != null)
{
Console.Write(cur.Data+" ");
cur = cur.Right;
}
// 再反转回来
ReverseRightBorder(tail);
}
/// 三、参考资料
[1]. https://zhuanlan.zhihu.com/p/348381217
[2]. https://zhuanlan.zhihu.com/p/101321696
[3]. https://www.bilibili.com/video/BV13g41157hK