python支持向量机回归_用libsvm进行回归预测
最近因工作需要,学习了台湾大学林智仁(Lin Chih-Jen)教授等人开发的SVM算法开源算法包。
为了以后方便查阅,特把环境配置及参数设置等方面的信息记录下来。
林教授年轻时照片
SVM属于十大挖掘算法之一,主要用于分类和回归。本文主要介绍怎么使用LIBSVM的回归进行数值预测。
LIBSVM内置了多种编程语言的接口,本文选择Python。
1 LIBSVM官方网址
可在这里下载LIBSVM的开源包,特别推荐初学者阅读文章A practical guide to SVM classification 和开源包自带的readme文件。可解决你的很多疑问。
2 安装环境
开源包版本 LIBSVM-3.20
操作系统 Win7 64bit
Python版本:python2.7.9 下载链接 https://www.python.org/downloads/
gnuplot: Gnuplot Version 5.0 (Jan 2015) 下载链接 http://sourceforge.net/projects/gnuplot/files/
3 回归预测
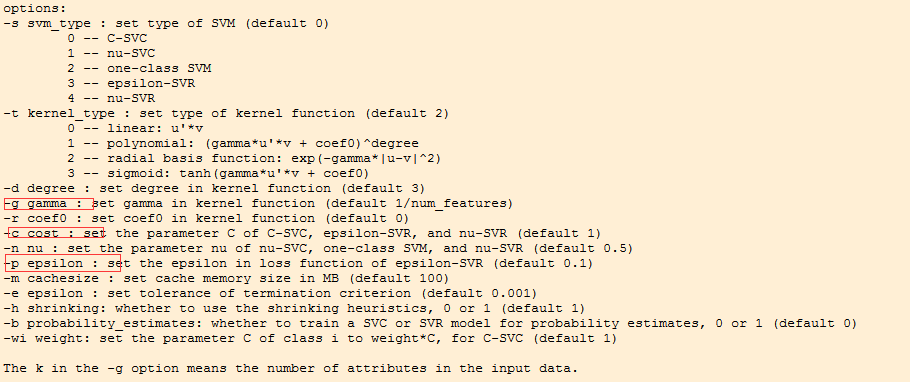
需要说明的是,回归预测需要gridsearch三个参数 gamma 、cost和epsilon;具体意义见下图红框。
开源包自带的grid.py 文件是针对分类用的,回归需要用gridregression.py文件。该文件需要另外下载。另外附带一份介绍LIBSVM使用的材料。 下载链接 http://pan.baidu.com/s/1bnfNmv9
下载完成后,把gridregression.py文件中的svm-train和gnuplot的安装路径修改为自己主机的安装路径。一定要认真,笔者在这里浪费好多时间。
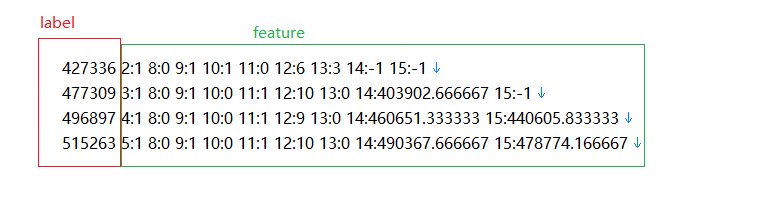
3.1 数据格式整理
3.2 归一化
回归预测需要对训练集trainset进行归一化,并对测试集testset进行同样的归一化。
$ svm-scale -y -1 1 -s scale train.txt > trainScale.txt
$ svm-scale -r scale test.txt > testScale.txt
-y 参数表示要对label进行归一化。可在cmd输入svm-scale 回车, 查看各参数的意义。
3.3 gridsearch 寻找最优参数
python gridregression.py -log2c -10,10,1 -log2g -10,10,1 -log2p -10,10,1 -v 10 -s 3 -t 2 trainScale.txt > trainrs.txt
-s 3 表示进行回归 -t 2 表示使用径向基核函数
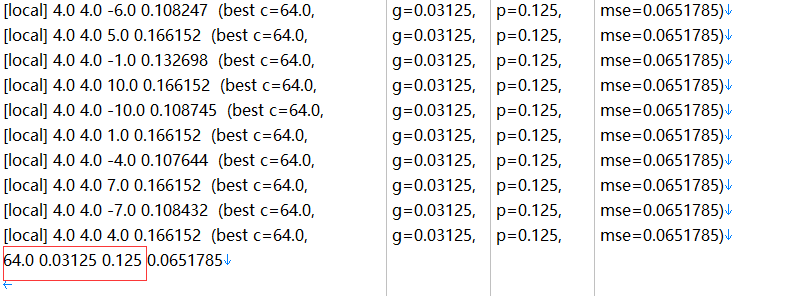
后查看trainrs.txt
红框中的三个数字对应最好的cost 、gamma和epsilon;
3.4 训练trainScale
svm-train -s 3 -t 2 -c 64 -g 0.03125 -p 0.125 trainScale.txt
会生成trainScale.txt.model 文件
3.5 预测testScale
svm-predict testScale trainScale.txt.model predict-result.txt
查看predict-result.txt内容
3.6 对结果反归一化
比如x属于原来的测试集, 范围是[min, max], 而scale后的范围是[m, n]
那么x对应归一化的值y是什么?y = (x-min)/(max-min) *(n-m) + m
那如果已知y, x又是多少呢?
x = (y-m)/(n-m) * (max-min) + min
可按照x = (y-m)/(n-m) * (max-min) + min 对predict-result.txt内容进行反归一化,从而得到最终的预测值。
4 model参数说明
![]()
其中, #iter 为迭代次数;
nu 是选择的核函数类型的参数;
obj 为SVM文件转换为的二次规划求解得到的最小值;
rho 为判决函数的偏置项b;
nSV 为标准支持向量个数(0
nBSV 为边界上的支持向量个数(a[i]=c);
Total nSV为支持向量总个数(对于两类来说, 因为只有一个分类模型Total nSV = nSV
但是对于多类, 这个是各个分类模型的nSV之和).
在目录下, 还可以看到产生了一个train.model文件, 可以用记事本打开, 记录了训练后的结果.
svm_type c_svc //所选择的svm类型, 默认为c_svc
kernel_type rbf //训练采用的核函数类型, 此处为RBF核
gamma 0.0769231 //RBF核的参数γ
nr_class 2 //类别数, 此处为两分类问题
total_sv 132 //支持向量总个数
rho 0.424462 //判决函数的偏置项b
label 1 -1 //原始文件中的类别标识
nr_sv 64 68 //每个类的支持向量机的个数
SV //以下为各个类的权系数及相应的支持向量
1 1:0.166667 2:1 3:-0.333333 … 10:-0.903226 11:-1 12:-1 13:1
0.5104832128985164 1:0.125 2:1 3:0.333333 … 10:-0.806452 12:-0.333333 13:0.5
………
-1 1:-0.375 2:1 3:-0.333333…. 10:-1 11:-1 12:-1 13:1
-1 1:0.166667 2:1 3:1 …. 10:-0.870968 12:-1 13:0.5
这里注意, 第二行出现的权系数为小数(0.5104832128985164)是因为这个点属于非边界上的支持向量, 即: (0