Python--利用张正友法进行相机标定

介绍

 ”张正友标定”是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。该方法介于摄影标定法和自标定法之间，克服了传统标定法需要的高精度标定物的缺点，又解决了自标定法鲁棒性差的难题。传统标定法需要三个两两垂直的平面，实验器材在操作过程中难以实现，而仅需使用一个打印出来的棋盘格就可以，并从不同方向拍摄几组照片即可。相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

一、基本原理

 相机标定的目的之一是为了建立物体从三维世界到二维成像平面上各坐标点的对应关系，所以首先我们需要定义这样几个坐标系：
（1）世界坐标系
世界坐标系是系统的绝对坐标系，是一个三维坐标系，为了描述目标物在真实世界里的位置而被引入。
（2）相机坐标系
在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，是以光轴与图像平面的交点为图像坐标系的原点所构成的直角坐标系。是一个作为沟通世界坐标系和图像坐标系的中间坐标系。
（3）像平面坐标系
二维坐标系，在一个图像平面中，以平面的中心像主点P为原点和坐标轴x,y组成了图片坐标系。是为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系
（4）像素坐标系
为了描述物体成像后的像点在数字图像上（相片）的坐标而引入，是真正从相机内读取到的信息所在的坐标系。

图片来源于

https://blog.csdn.net/a083614/article/details/78579163

 那么相机标定的一般过程为：
1、从世界坐标系转为相机坐标系，这一步是三维点到三维点的转换，包括相机外参R，t等参数；
2、从相机坐标系转为成像平面坐标系（像素坐标系），这一步是三维点到二维点的转换，包括相机内参K等参数；

接下来介绍一下实验所用到的棋盘
在黑白相间的棋盘格上，二维图像点很容易通过角点检测找到
实验中使用的棋盘是129的 棋盘格，每个方格边长是50mm，即含有118个角点
拍摄工具为：小米8

二、相机标定步骤

1、打印一张棋盘格，把它贴在一个平面上，作为标定物。
2、通过调整标定物或摄像机的方向，为标定物拍摄一些不同方向（这里拍摄15-20张）的照片。
3、从照片中提取棋盘格角点。（Harris角点）
4、估算理想无畸变的情况下，五个内参和六个外参。
5、应用最小二乘法估算实际存在径向畸变下的畸变系数。
6、极大似然法，优化估计，提升估计精度。

三、数学原理

（一）外参的计算

设三维世界坐标的点坐标为

二维相机平面的像素点为

齐次坐标为：

所以标定用的棋盘格平面到图像平面的单应性关系为：

其中：
S：世界坐标系到像平面坐标系的尺度因子
A：相机的内参矩阵
(u0,v0)： 像主点坐标
α, β: 焦距与像素横纵比的融合
γ: 径向畸变参数

 因为张正友法标定只需要一张棋盘格，因此我们不妨假设棋盘格位于Z=0，所以平移向量只有r1，r2 。。定义旋转矩阵R的第i列为 ri, 则有：

于是空间到图像的映射可改为：

 在这里描述的是空间中平面三维点和相机平面二维点之间的关系。因为相机平面中点的坐标可以通过图像处理的方式（如Harris角点）获取，而空间平面中三维点可以通过事先做好的棋盘获取。所以也就是说每张图片都可以计算出一个H矩阵
 其中H 是描述Homographic矩阵。H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H
令 H 为 H = [h1 h2 h3]

通过上述等式的矩阵运算，根据正交和归一化的约束可以得到如下等式：

外部参数可通过Homography求解，由 H = [h1 h2 h3] = λA[r1 r2 t]，可推出

（二）内参的计算

由r1和r2正交，且r1和r2的模相等，可以得到：
正交：

模相等：

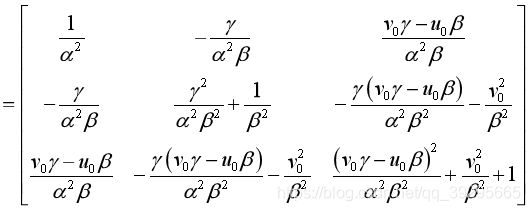
B 中的未知量可表示为6D 向量 b，由于B矩阵是个对称矩阵，所以可以写成一个6维向量形式：

设H中的第i列为 hi

根据b的定义，可以推导出如下公式

可以推导出

如果有n组观察图像，则V 是 2n x 6 的矩阵

根据推到的结果可知如果有n组观察图像，则V 是 2n x 6 的矩阵
根据最小二乘定义，V b = 0 的解是 VTV 最小特征值对应的特征向量。
因此, 可以直接估算出 b，可以通过b求解内参
因为B中的未知量为6个，所以当观测平面 n ≥ 3 时，可以得到b的唯一解
当 n = 2时, 一般可令畸变参数γ = 0
当 n = 1时, 仅能估算出α 与 β, 此时一般可假定像主点坐标 u0 与 v0 为0
B = ATA-1
B 是通过b构造的对称矩阵
内部参数可通过如下公式计算(cholesky分解)：

(三)最大似然估计

 上述的推导结果是理想情况下的解，但在实际操作过程中，由于可能存在噪声等一系列的影响，为了增加结果的可靠性，可以使用最大似然估计(Maximum likelihood estimation)来对上述的结果进行优化。
 假设同一个相机从n个不同的角度采集了n副包含棋盘格的图像进行定标，每个图像里有棋盘格角点m个。Mij表示第i幅图像上第j个像点对应的标定板上的三维点，则：

其中Ri和ti是第i副图对应的旋转矩阵和平移向量，K是内参数矩阵

则角点mij的概率密度函数为：

构造似然函数：

为了能够让L取得最大值，需要最小化下面的值

这里使用的是多参数非线性系统优化问题的Levenberg-Marquardt算法进行迭代求最优解。

（四）畸变

 拍照时通常要在相机的镜头前添加透镜，在相机成像的过程中，透镜会对光线的传播产生影响，从而影响相机的成像效果，产生了畸变
 畸变主要分为两种：径向畸变、切向畸变（畸变是相机本身的特性，与内参无关，标定一次后即可）

径向畸变来自于透镜形状。
切向畸变来自于整个摄像机的组装过程。

1、径向畸变：

 透镜自身的形状对才光线的传播产生影响，实际摄像机的透镜总是在成像仪的边缘产生显著的畸变，这种现象来源于“筒形”或“鱼眼”的影响。
 在针孔相机模型中，一条直线在成像平面上的像仍然是直线。但是在实际拍摄的过程中，由于透镜的存在，一条直线往往被投影成了曲线，当拍摄的角度越靠近图像的边缘，这种现象越明显。因为透镜是中心对称的，所以这种不规则的畸变通常是径向对称的。主要有两大类：桶形畸变和枕形畸变。如图

对于径向畸变可以通过下面的泰勒级数展开式进行校正。这里不做阐述。

2、切向畸变：

由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的。

3、径向畸变估计

参考博客

https://www.cnblogs.com/wangguchangqing/p/8335131.html#autoid-2-3-0

 在张氏定标法中，只关注了影响最大的径向畸变。
假设，(μ,ν)是理想的无畸变的像素坐标；(μ^,ν ^)是畸变后的像素坐标；(μ0,ν0)是相机的像主点；(x,y)和(x ^,y ^)理想的无畸变的归一化的图像坐标和畸变后的归一化图像坐标，数学表达为：

其中，k1,k2表示径向畸变的系数。

矩阵形式：

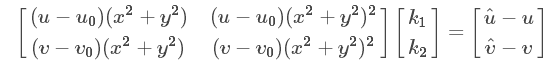
记做：Dk=d
则可得：

计算得到畸变系数k。
使用最大似然的思想优化得到的结果，即像上一步一样，LM法计算下列函数值最小的参数值：

得到畸变参数k1,k2后，可以先将图像进行去畸变处理，然后用去畸变后的图像坐标估计相机的内参数。

四、实现

（一） matlab实现

1、应用程序中找到Camera Calibration

2、添加标定板拍摄图片

3、输入棋盘格每格的尺寸大小

4、点击Calibration，开始标定。

5、得到标定结果

6、结果


每一幅图像都有一个外参矩阵，它通过将棋盘格上坐标系上的角点坐标（x,y,0,1）（计算过程中设定参考坐标系在棋盘格上左上方角点，Z轴垂直棋盘格平面，因此z为0,1表示齐次坐标）左乘外参矩阵再左乘内参矩阵可以得到该外参矩阵对应图像中的相应角点坐标

（二） python实现

# -*- coding: cp936 -*-
import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((5*9,3), np.float32)
objp[:,:2] = np.mgrid[0:9,0:5].T.reshape(-1,2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob(r"C:\Users\WeiLinLin\PycharmProjects\untitled\data\chess\*.jpg")
i=0;
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (11, 8), None)
    #print(corners)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (11, 8), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i+=1;
        cv2.imwrite('conimg'+str(i)+'.jpg', img)
        cv2.waitKey(4000)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
print ("dst的大小为:", dst1.shape)

实验结果：

mtx为内参矩阵，dist为畸变参数：

rvecs为旋转向量：

畸变矫正：