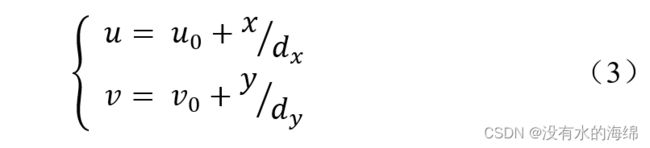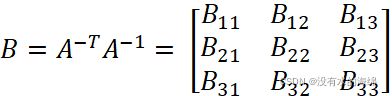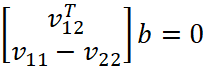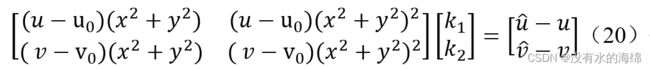基于张正友标定法的工业机器人视觉标定

二、机器人视觉模型

机器人视觉系统的标定其实是获取摄像机坐标系（ICS）与机器人坐标系（RCS）之间转换关系的过程，在标定机器人视觉系统（Eye-to-Hand）之前，首先要对摄像机进行标定。通常摄像机镜头会存在径向、切向和偏心等畸变，因此需要选择合适的畸变模型对摄像机进行标定。工业镜头的畸变主要维径向畸变，可以用线性畸变模型表示。生活上使用的摄像头还会有切向和偏心等畸变，需要使用非线性模型。对于工业摄像头，如果使用非线性畸变模型，将会大大增加计算复杂度而且标定精度不会提高。因此本文在论述中采用线性畸变模型来标定机器人视觉系统。

张正友提出了基于单平面棋盘格的相机标定方法，该方法标定的精度高、只需一个平面棋盘格标定板，标定过程中相机要拍摄2张以上标定板图片，且不需知道标定板具体运动参数。

2.1摄像机成像原理

常见的工业相机成像模型，可以称为小孔成像模型。被拍摄景物穿过摄像机镜头，通过光轴中心点，会在成像平面形成比例缩小、左右和上下都相反的实像。其中摄像机光轴的中心点，指的是摄像机镜头的光心。为方便理解，可将工业相机的成像模型转化为如图1所示的小孔成像模型，相机的镜头可以被理解为一个小孔。

如图1所示，平面 Π１（世界坐标系）是被拍摄物体所在平面，摄像机的光轴中心点为Oc（摄像机坐标系原点），摄像机的成像平面为Π２′（图像坐标系平面）， Π２ 是摄像机等小孔成像相机模型等效成像平面。由摄像机的小孔成像模型可以知道，物体反射的光线经过摄像机的光学中心，在成像平面Π２′ 上呈现的物体图像，与原物体进行比较，方向相反，比例缩小。在对获取的数学图像进行信息处理时，可先将原图像等比例放大，并对图像进行反转，可用平面Π２ 代替平面Π２′ 做一个等效处理，再对平面 Π２ 上的等效像进行放大处理，便得到想要的数字图像。

2.2 摄像机标定原理

在相机的几何模型下，可以将三维物体的坐标转化为二维图像的坐标，通常需要建立以下几种坐标系：世界坐标系、图像坐标系、摄像机坐标系。其中，图像坐标系根据单位尺度的不同又可以分为图像像素坐标系和图像物理坐标系，两者区别在于图像像素坐标系以像素为单位尺度，图像物理坐标系是以物理长度为单位尺度。其标定模型如图所示。

图2 机器人视觉标定模型

图2中，(Oc,Xc,Yc,Zc)为摄像机坐标系（CCS），Oc为摄像机的投影中心，z轴与摄像机的主光轴重合；(Ow,Xw,Yw,Zw)为机器人坐标系（世界坐标系WCS）；(Oi,Xi,Yi)为成像平面坐标系（IPCS）；(Ou,Xu,Yu)为图像坐标系（ICS）。空间一点P在CCS下的坐标为P(xc,yc,zc)；在WCS下的坐标为P(xw,yw,zw)。若不考虑畸变，则点P以透视投影在成像平面投影，投影点为Pn(xn,yn)；若考虑径向畸变，镜头的畸变将导致P发生偏移，投影点为 (xi,yi)。

2.2.1　世界坐标系

摄像机能够存在于三维空间的任一位置，因此有必要在三维空间中建立一个坐标系，作为摄像机和景物的参照坐标系，称之为世界坐标系（XwOwYw）。假设成像点P（xw, yw, zＷ）为三维空间（世界坐标系）中的一个随机点，则世界坐标系（XwOwYw）和摄像机坐标系系（XcOcYc）之间存在如下的转换表达式：

式中： T 为 3×1 的平移向量；R 为 3×3 的正交旋转矩阵，满足的约束条件：

2.2.2　摄像机坐标系

摄像机坐标系 (XcOcYc) 是以相机的光心为坐标原点，Xc、Yc轴平行于图像物理坐标系X、Y轴，并取相机光轴为Zc轴建立的三维直角坐标系。由图２再结合三角测量原理，图像物理坐标系 (XOY) 与摄像机坐标系 (XcOcYc) 之间存在如下的转换表达式：

如果用齐次坐标和矩阵的形式实现，即:

 2.2.3　图像坐标系

在图像坐标系中，假设 (u，v) 分别表示图像像素坐标系中的横、纵坐标，而 (u0，v0) 则表示像素坐标系中心点的位置坐标，dx、dy分别表示每个像素在图像物理坐标系x轴和y轴上的物理尺寸大小，那么，图像像素坐标系（XfOfYf）和图像物理坐标系（XOY）之间存在如下的转换表达式：

其矩阵形式为：

综合（1）、（4）、（5）可得：

 式中：A为内部参数，由fx、fy、u0、v0决定；[R|t]为外部参数，由摄像机在世界坐标系中的位置决定，即由正交旋转矩阵R和平移向量T共同决定。通过摄像机成像模型。在已知相机参数的情况下，可以求得相机未知参数，这个过程也就是摄像机标定。A[R|t]共有9个未知因子，至少需要空间上已知的5个特征点才能求解所以未知因子。 

2.2.4　摄像头镜头畸变

通过以上三步得到的模型是基于理想光学系统，而在实际的工业场景中，理想条件并不存在，相机镜头会产生畸变。理想状态下，物体和其影像之间的放大倍率k是固定的，但在工业环境中，物体和其影像之间的放大倍率k往往并不是固定，而是一些有关视场角的函数[14-15]，这种非线性的变化，称为畸变。因此，在相机标定时，必须要考虑镜头的畸变，并采取相应的措施来降低误差，提高视觉系统的整体精度。

如图３所示，径向畸变指的是光心系统中，光线穿过镜头，在远离光心的位置比靠近光心的位置更加弯曲，根据弯曲方向，可分为枕形畸变（a）和桶形畸变（b）两种形式。

 图 ３　径向畸变

为矫正径向畸变，可以先建立二阶透镜的径向畸变模型：

         （８）

式中：（u′，v′）为无畸变的理想图像坐标，（u，v）为实际图像坐标，（u0，v0）为光轴中心点的图像坐标，k′u和k′v分别为u和v方向上的二阶畸变系数，r为图像到参考点的距离，且满足：

             （9）

2.3 参数求解过程

2.3.1 单应矩阵求解

在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面 Π；其在成像平面的像是另一个平面 π，由于棋盘格的角点是已知的，我们可以通过角点提取算法获得图像中的角点，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵H。

通过（7）式可得相机模型为可以得到下面的等式：

H = A[R|t]                  （10）

H 表示的是成像平面和标定棋盘平面之间的单应矩阵。通过对应的点对解得H后，则可以通过上面的等式得到相机的内参数 A，以及外参旋转矩阵R和平移向量 t。设棋盘格所在的平面为世界坐标系中Z = 0的平面，则相机模型可变为：

（11）

式中：  为旋转矩阵R的第i列。整合公式（7）和公式（11），可以得到单应矩阵H和相机矩阵之间的关系：

这样就能通过单应矩阵H来约束相机的内参和外参，知道单应矩阵H便可计算出相机的内参和外参。H的计算是使实际图像坐标mi = [u,v]T和根据相机模型计算出的图像坐标mi 之间残差最小的过程，目标函数为：

                （13）

2.3.2相机内外参数求解

求解出矩阵H后，可以得到:

          （14）

令

       （15）

有

                        （16）

其中:

               （17）

式（14）可以改写为：

             （18）

对标定板拍摄了n幅图像，将这n个方程组叠起来，可得Vb=0。当b求解后，就可以求出矩阵A，以上述结果为初值，进行优化搜索，从而计算出相机的所有内参数准确值。一般采集5～9幅图像就可以取得较好的标定结果。得到矩阵A后，可得到相机外部参数Ｒ、T:

                                         （19）                

2.3.3 畸变系数求解

经过整理，可以得到关于k1和k2矩阵形式的方程：

利用最小二乘法可以求解畸变系数k1和k2。

三、代码实现

本文采用了一种基于OpenCV的机器视觉标定方法，采用张正友标定法进行相机标定，以棋盘图像作为标定的参照物，实现了世界坐标系与图像坐标系之间的转换。OpenCV是一个开源机器视觉库，它包含了数百种计算机视觉算法，在工业中运用十分广泛。调用opencv库内的findChessboardCorners、cornerSubPix、calibrateCamera等函数实现张正友标定，得出相机的内参和外参。

3.1 实验流程

① 打印一张棋盘格A4纸张，并贴在一个平面上；

② 针对棋盘格拍摄若干张图片（一般10~20张）；

③ 在图片中检测特征点（Harris角点）；

④ 根据角点的位置信息及图像中的坐标，求解H单应矩阵；

⑤ 利用解析解估算方法计算出5个内部参数以及6个外部参数；

⑥ 根据极大似然估计策略，设计优化目标并实现参数的优化。

3.2 程序流程图

首先进行初始化，声明变量、定义其类型和初始值，设置角点的数量。

接下来进入循环结构：读取第i张图片的图像信息；灰度化处理。在像素坐标系下寻找角点（特征点），如果找到，返回ret为true且将角点的坐标存到数组变量corner内；否则，ret为false。而后将角点的像素坐标系下的坐标转换为亚像素系下的坐标。得到精确的坐标位置后，绘制角点，保存图片。进入下次循环……

循环结束后，得到角点的实际位置均储存在列表变量obj_points内。调用摄像机标定函数进行标定，得到摄像机的内参和外参。最后，对图片进行校正。如图4所示。

图 4 程序流程图

3.3 关键API介绍

3.3.1

ret, corner = cv2.findChessboardCorners (image, patternSize, corners, flags = None)

3.3.1.1函数功能

此函数试图确定输入图片是否有棋盘图案，并定位棋盘板上的角点。如果所

有的角点被找到且以一定的顺序排列（一行接一行，从一行的左边到右边），该函数会返回1且将角点位置储存到corner内。如果该函数没有找到所有的角点或者重新排列他们，则返回0。

3.3.1.2 参数解析

第一个参数Image是输入原始的棋盘板图像。该图像必须是一张8位的灰度图或色彩图。

第二个参数patternSize=(w,h)，棋盘上每一排和每一列的角点个数；w = 棋盘板一行上黑白块的数量 - 1，h = 棋盘板一列上黑白块的数量 - 1。

第三个参数Corners为检测到的角点的输出数组。

第四个参数Flags表示不同的操作标记，为0或者以下值的组合。CALIB_CB_ADAPTIVE_THRESH，使用自适应阈值法把图像转换为黑白图，而不是使用一个固定的阈值。CALIB_CB_NORMALIZE _IMAGE，在利用固定阈值或自适应阈值法二值化图像之前，利用直方图均衡化图像。CALIB_CB_FILTER_QUADS，使用额外的标准(如轮廓面积，周长，正方形形状)来过滤掉在轮廓检索阶段提取的假四边形。CALIB_CB_FAST_CHECK，对图像运行一个快速检查机制以查找棋盘板的角点，如果没有找到角点则返回一个快捷提醒。当没有观察到棋盘时，可以极大地加快在退化条件下的调用。

3.3.1.3 具体使用

ret, corners = cv2.findChessboardCorners(gray, (4, 6), None)，其中gray为灰度化的图片，图像内共有5行7列方块故设置（w，h）=（4，6）。

3.3.2

corners2 = cv2.cornerSubPix (image, corners, winSize, zeroZone, criteria )

3.3.2.1 函数功能

cv2.findChessboardCorners()提取到的角点只能达到像素级别，在很多情况下并不能满足实际的需求，这时，我们则需要使用cv2.cornerSubPix()对检测到的角点作进一步的优化计算，可使角点的精度达到亚像素级别。

3.3.2.2 参数解析

第一个参数image是输入图像，和cv2.findChessboardCorners() 中的输入图像是同一个图像。

第二个参数corner是检测到的角点，即是输入也是输出。

第三个参数winSize是计算亚像素角点时考虑的区域的大小，大小为N×N; N=(winSize*2+1)。

第四个参数zeroZone作用类似于winSize，但是总是具有较小的范围，通常忽略（即Size(-1, -1)）。

第五个参数criteria用于表示计算亚像素时停止迭代的标准，可选的值有cv2.TERM_CRITERIA_MAX_ITER、cv2.TERM_CRITERIA _EPS（可以是两者其一，或两者均选），前者表示迭代次数达到了最大次数时停止，后者表示角点位置变化的最小值已经达到最小时停止迭代。二者均使用cv2.TermCriteria()构造函数进行指定。

3.3.2.3 具体使用

corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)，其他参数依据参数定义可得，迭代规则criteria = (cv2.TERM_ CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)，采用的停止准则是最大循环次数30和最大误差容限0.001。

3.3.3

retval, cameraMatrix, distCoeffs, rvecs, tvecs = cv2.calibrateCamera (objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]])

3.3.3.1 函数功能

获取到棋盘标定图的内角点图像坐标之后，就可以使用cv2.calibrateCamera()函数进行标定，标定的结果是生成相机的内参矩阵cameraMatrix、相机的5个畸变系数distCoeffs，另外每张图像都会生成属于自己的平移向量和旋转向量。

3.3.3.2 参数解析

第一个参数objectPoints，为世界坐标系中的三维点。需要依据棋盘上单个黑白矩阵的大小，计算出（初始化）每一个内角点的世界坐标；

第二个参数imagePoints，为每一个内角点对应的图像坐标点；

第三个参数imageSize，为图像的像素尺寸大小，在计算相机的内参和畸变矩阵时需要使用到该参数；

第四个参数cameraMatrix为相机的内参矩阵；

第五个参数distCoeffs为畸变矩阵；

第六个参数rvecs为旋转向量；

第七个参数tvecs为位移向量；

第八个参数flag为标定时所采用的算法。有如下几个参数： CV_ CALIB_USE_INTRINSIC_GUESS：使用该参数时，在cameraMatrix矩阵中应该有fx,fy,u0,v0的估计值。否则的话，将初始化(u0,v0）图像的中心点，使用最小二乘估算出fx，fy。CV_CALIB_FIX_PRINCIPAL_ POINT：在进行优化时会固定光轴点。当CV_CALIB_USE_ INTRINSIC_GUESS参数被设置，光轴点将保持在中心或者某个输入的值。CV_CALIB_FIX_ASPECT_RATIO：固定fx/fy的比值，只将fy作为可变量，进行优化计算。当CV_CALIB _USE_INTRINSIC_ GUESS没有被设置，fx和fy将会被忽略。只有fx/fy的比值在计算中会被用到。CV_CALIB_ZERO_ ANGENT_DIST：设定切向畸变参数（p1,p2）为零。 CV_CALIB_FIX_K1,…,CV_CALIB_FIX_K6：对应的径向畸变在优化中保持不变。 CV_CALIB_RATIONAL_MODEL：计算k4，k5，k6三个畸变参数。如果没有设置，则只计算其它5个畸变参数。

第九个参数criteria是最优迭代终止条件设定。

3.3.3.3 具体使用

ret,mtx,dist,rvecs,tvecs=cv2.calibrateCamera(obj_points, img_points, (4,6), None, None)

3.4 实验结果分析

3.4.1 角点描绘

将打印好的棋盘格摆放在桌子上，使用手机选取不同方向、不同角度拍摄，得到如图5所示的九张棋盘格图片。从每幅图像中提取角点，根据棋盘格世界坐标系和图像坐标系的对应关系，从而计算出摄像机的内外参数。棋盘格提取角点特征点后描绘出角点，可得图6 ，其中第一张棋盘格图片描写角点后的图像为图7。

图 5 棋盘格原图

图 6 棋盘格描写角点后的图片集

图 7  chess1.jpg

3.4.2 参数计算

内参数为摄像机的内部参数，每个摄像机的内参数是常数；畸变系数为径向、切向和偏心等畸变系数组合，也是常数；外参数是因为拍摄角度不同每张图片的旋转向量和平移向量不同。程序的输出参数如下所示。

内参数矩阵mtx:

 [[2.91468683e+03 0.00000000e+00 1.94038016e+03]

  [0.00000000e+00 2.83229610e+03 1.61197119e+03]

  [0.00000000e+00 0.00000000e+00 1.00000000e+00]]

畸变系数(k1,k2,p1,p2,k3) dist:

 [[-0.02298863 -0.00650227 -0.00700737 -0.00276018  0.06569634]]

外参数矩阵_旋转向量rvecs:

 [ array([[-0.36854373],[0.3555173],[1.56045954]]),

array([[-0.5606113],[0.09088327],[1.21231929]]),

array([[-0.70682603],[0.72363556],[1.44056577]]),

array([[-0.30600564],[0.83994047],[2.41910773]]),

array([[0.27302596],[-0.78684309],[-3.09086458]]),

array([[0.27502860],[-0.26202514],[1.59608024]]),

array([[-0.25667161],[0.39806505],[0.08720637]]),

array([[-0.62018569],[0.79027612],[1.58435601]]),

array([[-0.09777943],[0.92009288],[2.38136981]])]

外参数矩阵_平移向量tvecs:

 [ array([[ 4.74481865], [-2.91692768], [11.14771434]]),

array([[ 4.57328302], [-3.77500684], [15.47054046]]),

array([[ 5.03508063], [-2.27991628], [12.85376274]]),

array([[ 3.52513602], [-0.25721530], [ 9.90898221]]),

array([[ 3.32522672], [1.349679470], [9.89923642]]),

array([[ 4.70361013], [-2.62093839], [9.98977229]]),

array([[-3.59163554], [-4.31874367], [12.47920915]]),

array([[ 4.57129566], [-2.00441497], [12.37520349]]),

array([[ 4.06044504], [-0.84523968], [10.17817862]])]

3.4.3 棋盘格矫正

相机标定后得到摄像机的内参、外参和畸变系数，可以对图片进行校正，校正前后的图片如图8所示。

图 8 标定图片前后对图

五、参考文献

[1]付贵.基于机器视觉的工业机器人标定方法研究[J].南方农机,2018,49(09):147-148.

[2]陈为,李泽辰,张婧,钟欣童.基于HALCON的工业机器人视觉系统标定方法研究[J].电子测量技术,2020,43(21):137-141.

[3]宋岳秦,卢军,孙姝丽.基于HALCON的机器人视觉系统标定方法研究[J].南方农机,2018,49(20):47-49.

---

 本文所用程序：

使用张正友标定法对工业机器人中视觉标定的python实现（可直接运行）-机器学习文档类资源-CSDN文库