第二门课:改善深层神经网络:超参数调试、正则化以及优化(第二周)——优化算法
优化算法
- 1. Mini-batch 梯度下降
- 2. 理解 mini-batch 梯度下降
- 3. 指数加权平均数
- 4. 理解指数加权平均数
- 5. 指数加权平均的偏差修正
- 6. 动量Momentum梯度下降法
- 7. RMSprop
- 8. Adam 优化算法
- 9. 学习率衰减
- 10. 局部最优的问题
1. Mini-batch 梯度下降
在巨大的数据集上进行训练,速度非常慢,如何提高效率?
前面我们学过向量化可以较快的处理整个训练集的数据,但是如果样本非常的大,在进行下一次梯度下降之前,你必须完成前一次的梯度下降。如果我们能先处理一部分数据,算法速度会更快。
把训练集分割为小一点的子集(称之 mini-batch)训练,即Mini-batch 梯度下降。
对比:
- batch 梯度下降法:指的就是前面讲的梯度下降法,每次需要同时处理整个训练集
- mini-batch梯度下降:每次处理的是单个的 mini-batch 训练子集
2. 理解 mini-batch 梯度下降
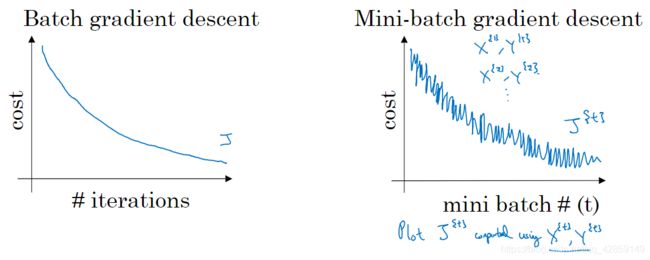
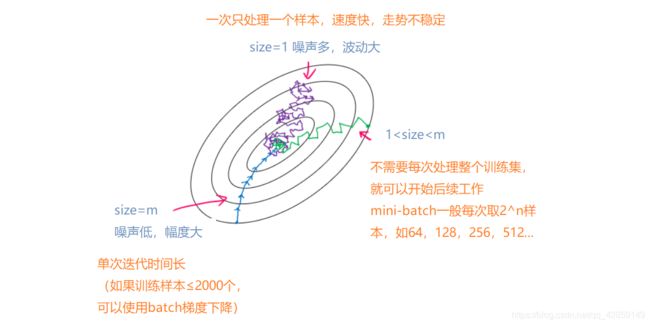
mini-batch 梯度下降,每次迭代后 cost 不一定是下降的,因为每次迭代都在训练不同的样本子集,但总体趋势应该是下降的。
mini-batch 的 size 大小:
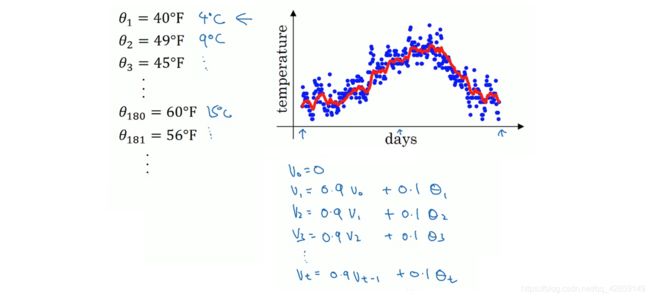
3. 指数加权平均数
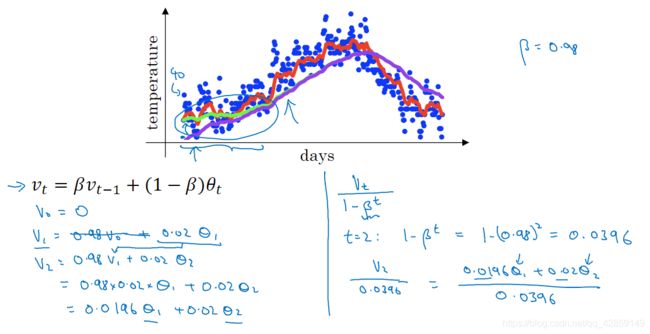
假设, v 0 = 0 , v t = β ∗ v t − 1 + ( 1 − β ) ∗ θ t v_0 = 0,v_t = \beta*v_{t-1}+(1-\beta)*\theta_t v0=0,vt=β∗vt−1+(1−β)∗θt,选取不同的 β \beta β 值,得到相应的气温曲线。
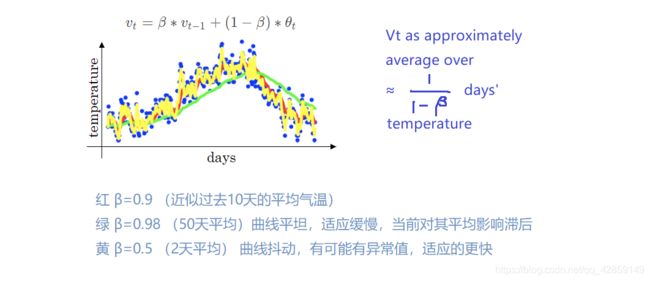
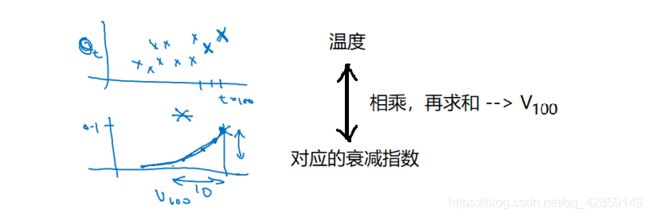
4. 理解指数加权平均数
假如 β = 0.9 , t = 100 \beta = 0.9,t=100 β=0.9,t=100,将上面的带进去求 v 100 v_{100} v100
v 100 = 0.1 θ 100 + 0.9 ( 0.1 θ 99 + 0.9 ( 0.1 θ 98 + 0.9 v 97 ) ) 0 v_{100}=0.1 \theta_{100}+0.9\left(0.1 \theta_{99}+0.9\left(0.1 \theta_{98}+0.9 v_{97}\right)\right)_{0} v100=0.1θ100+0.9(0.1θ99+0.9(0.1θ98+0.9v97))0
v 100 = 0.1 θ 100 + 0.1 × 0.9 θ 99 + 0.1 × ( 0.9 ) 2 θ 98 + 0.1 × ( 0.9 ) 3 θ 97 + 0.1 × ( 0.9 ) 4 θ 96 + … v_{100}=0.1 \theta_{100}+0.1 \times 0.9 \theta_{99}+0.1 \times(0.9)^{2} \theta_{98}+0.1 \times(0.9)^{3} \theta_{97}+0.1 \times(0.9)^{4} \theta_{96}+\ldots v100=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+0.1×(0.9)4θ96+…
v θ = 0 , v t : = β ∗ v θ + ( 1 − β ) ∗ θ t v_\theta = 0,v_t := \beta*v_\theta+(1-\beta)*\theta_t vθ=0,vt:=β∗vθ+(1−β)∗θt
当然,它并不是最好、最精准的计算平均数的方法。
5. 指数加权平均的偏差修正
6. 动量Momentum梯度下降法
介绍:与 SDG 结合使用的一种常用方法叫做 Momentum。Momentum 不仅会使用当前梯度,还会积累之前的梯度以确定走向。
思想:计算梯度的指数加权平均数,利用该梯度更新权重。

上图情况下,标准的梯度下降会上下波动,且要使用较小的学习率,否则会偏离更远。
如果我们使用过去梯度的加权平均,纵向的就抵消了一些,横向的叠加了一些,可以更平滑的快速找向最优点
v d W = β v d W + ( 1 − β ) d W v d b = β v d b + ( 1 − β ) d b W : = W − α ∗ v d W b : = b − α ∗ v d b \begin{aligned} v_{d W}&=\beta v_{d W}+(1-\beta) d W \\ v_{d b}&=\beta v_{d b}+(1-\beta) d b \\ \\ W&:=W-\alpha * v_{d W} \\ b&:=b-\alpha * v_{d b} \end{aligned} vdWvdbWb=βvdW+(1−β)dW=βvdb+(1−β)db:=W−α∗vdW:=b−α∗vdb
- 超参数有 α , β ( β \alpha,\beta (\beta α,β(β 经常取 0.9)
- 如果想偏差修正, v d W , v d b v_{d W},v_{d b} vdW,vdb 还要除以 1 − β t 1-\beta^{t} 1−βt,实际上人们不这么做,10次迭代之后,偏差就基本很小了
- 在实际使用过程中,往往会把 ( 1 − β ) (1-\beta) (1−β)去掉
动量梯度下降法,并不是对所有情况都有效,它对碗状的优化效果较好
7. RMSprop
全称是 root mean square prop 算法,它也可以加速梯度下降
微分平方的加权平均数:
S d W = β S d W + ( 1 − β ) ( d W ) 2 S d b = β S d b + ( 1 − β ) ( d b ) 2 W : = W − α ∗ d W S d W + E b : = b − α ∗ d b S d b + E \begin{aligned} S_{d W}&=\beta S_{d W}+(1-\beta)(d W)^{2}\\ S_{d b}&=\beta S_{d b}+(1-\beta)(d b)^{2}\\\\ W&:=W-\alpha * \frac{d W}{\sqrt{S_{d W}}+\mathcal{E}}\\ b&:=b-\alpha * \frac{d b}{\sqrt{S_{d b}}+\mathcal{E}}\\ \end{aligned} SdWSdbWb=βSdW+(1−β)(dW)2=βSdb+(1−β)(db)2:=W−α∗SdW+EdW:=b−α∗Sdb+Edb
E = 1 e − 8 \mathcal{E} = 1e^{-8} E=1e−8 保证分母不为 0
RMSprop 跟 Momentum 有很相似的一点,可以消除梯度下降和mini-batch梯度下降中的摆动,并允许你使用一个更大的学习率,从而加快你的算法学习速度。
8. Adam 优化算法
Adam (Adaptive Moment Estimation) 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起
初始化: v d W = 0 , S d W = 0 , v d b = 0 , S d b = 0 v_{d W}=0, S_{d W}=0, v_{d b}=0, S_{d b}=0 vdW=0,SdW=0,vdb=0,Sdb=0
t 次迭代
Momentum:
v d W = β 1 v d W + ( 1 − β 1 ) d W v d b = β 1 v d b + ( 1 − β 1 ) d b \begin{aligned} v_{d W}&=\beta_{1} v_{d W}+\left(1-\beta_{1}\right)dW\\ v_{d b}&=\beta_{1} v_{d b}+\left(1-\beta_{1}\right)db \end{aligned} vdWvdb=β1vdW+(1−β1)dW=β1vdb+(1−β1)db
RMSprop:
S d W = β 2 S d W + ( 1 − β 2 ) ( d W ) 2 S d b = β 2 S d b + ( 1 − β 2 ) ( d b ) 2 \begin{aligned} S_{d W}&=\beta_{2} S_{d W}+\left(1-\beta_{2}\right)(d W)^{2}\\ S_{d b}&=\beta_{2} S_{d b}+\left(1-\beta_{2}\right)(d b)^{2} \end{aligned} SdWSdb=β2SdW+(1−β2)(dW)2=β2Sdb+(1−β2)(db)2
偏差修正:
v d W corrected = v d W 1 − β 1 t v d b corrected = v d b 1 − β 1 t S d W corrected = S d W 1 − β 2 t S d b corrected = S d b 1 − β 2 t \begin{aligned} v_{d W}^{\text {corrected }}&=\frac{v_{d W}}{1-\beta_{1}^{t}}\\ v_{d b}^{\text {corrected }}&=\frac{v_{d b}}{1-\beta_{1}^{t}}\\ S_{d W}^{\text {corrected }}&=\frac{S_{d W}}{1-\beta_{2}^{t}}\\ S_{d b}^{\text {corrected }}&=\frac{S_{d b}}{1-\beta_{2}^{t}} \end{aligned} vdWcorrected vdbcorrected SdWcorrected Sdbcorrected =1−β1tvdW=1−β1tvdb=1−β2tSdW=1−β2tSdb
更新权重:
W : = W − α ∗ v d W corrected S d W corrected + ε b : = b − α ∗ v d b correted S d b corrected + ε \begin{aligned} W&:=W- \alpha*\frac{ v_{d W}^{\text {corrected }}}{\sqrt{S_{d W}^{\text {corrected }}}+\varepsilon}\\ b&:=b- \alpha*\frac{v_{\mathrm{db}}^{\text {correted }}}{\sqrt{S_{\mathrm{db}}^{\text {corrected }}}+\varepsilon} \end{aligned} Wb:=W−α∗SdWcorrected +εvdWcorrected :=b−α∗Sdbcorrected +εvdbcorreted
Adam算法结合了 Momentum 和 RMSprop 梯度下降法,并且是一种极其常用的学习算法
其被证明能有效适用于不同神经网络,适用于广泛的结构
9. 学习率衰减
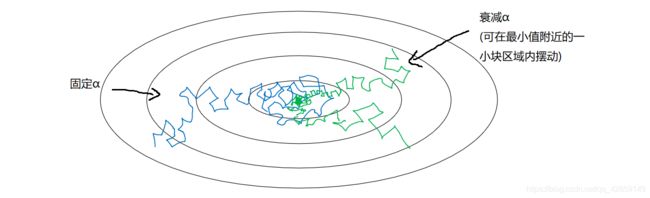
慢慢减少 学习率 的本质在于,在学习初期,使用较大的步伐,开始收敛的时候,用小一些的学习率能让步伐小一些
- 对不同的 mini-batch 进行训练,一次称之为 epoch
α = 1 1 + decayRate ∗ epochNum ∗ α 0 \alpha=\frac{1}{1+\text { decayRate } * \text { epochNum }} * \alpha_{0} α=1+ decayRate ∗ epochNum 1∗α0
还有些其他的方法:
α = 0.9 5 epochNum α 0 α = k e p o c h N u m α 0 α = k t α 0 , t 为mini-batch的数字 \begin{gathered} \alpha=0.95^{\text {epochNum }} \alpha_{0} \\ \alpha=\frac{k}{\sqrt{e p o c h N u m}} \alpha_{0} \\ \alpha=\frac{k}{\sqrt{t}} \alpha_{0}, t \text { 为mini-batch的数字 } \end{gathered} α=0.95epochNum α0α=epochNumkα0α=tkα0,t 为mini-batch的数字
还有离散下降学习率, 即 不是每步都下调学习率
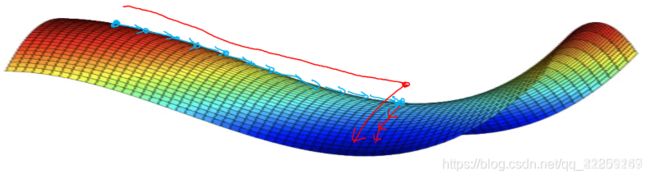
10. 局部最优的问题
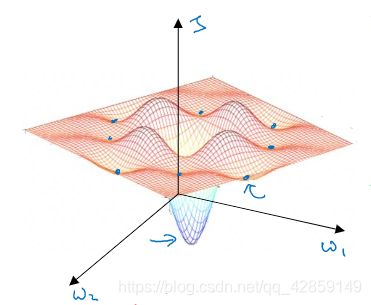
高维度空间中,我们不太可能遇见(概率很低)如上图所示的局部最优点,因为需要这么多的维度方向上都梯度为 0(概率很低)
所以更有可能遇到的是鞍点
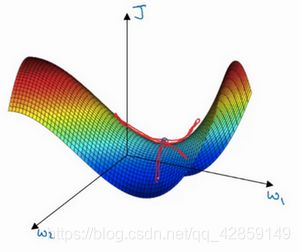
基本不会遇见局部最优问题,可能遇见的是平稳段减缓了学习速度,该区域梯度接近于 0 ,要很长时间才能走出去。Momentum 或 RMSprop,Adam 能够加快速度,让你尽早 走出平稳段。