视觉SLAM十四讲学习笔记——第八讲 视觉里程计(3)
前文提到的特征点法基本过程为:
(1)提取关键点并计算描述子,得到特征点后进行两幅图像间的匹配。
(2)构建最小二乘问题:最小化重投影误差(图像平面上或者世界坐标系下)。
(3)迭代优化求出最优解,确定摄像机运动参数。
上述过程中,特征点的提取最为耗时,因为要遍历整场图像并计算描述子。因此这一章引出了光流法和直接法,二者都是基于“最小光度误差”进行求解,但解决问题的方法不同:
光流法:本质上是替代图像间特征点匹配的过程,使用“灰度不变”的假设确定关键点的对应关系,因此使用时仅需要对第一幅图像提取关键点,不需要计算描述子,显著缩短运算时间。在完成匹配后,使用特征点法相同的方式估计摄像机运动参数。至于使用哪种方法,要根据是否已知图像点的深度信息来选择。
直接法:直接法则是抛开关键点的提取,直接选择图像中的随机点甚至是全部点(注意不要选择图像边界附近的点),基于“灰度不变”假设构建最小二乘问题:最小化光度误差,直接优化求解两幅图像间相机的运动参数。使用直接法时往往需要已知初始图像的深度信息。
在书中的理论分析过程和示例代码中也有一些需要注意的地方:
1.超定线性方程的最小二乘解:
P210提到了关于相机运动的超定线性方程并给出了其最小二乘解,事实上这个问题和P126的问题如出一辙,我在之前的文章中有过证明,但是证明过程有一些问题也后续补充了,这里再推导一次。视觉SLAM十四讲学习笔记——第六讲 非线性优化(1)_晒月光12138的博客-CSDN博客
首先还是要明确两个求导公式:
设定待求解问题:
推导过程:
其实这个推导属于给自己找麻烦了,没必要非要弄一个中间变量,大可以代入之后直接求导,只是在实践过程中突然发现了这个问题,就是对于数值、向量、矩阵中间的求导问题,以及链式法则的变化。
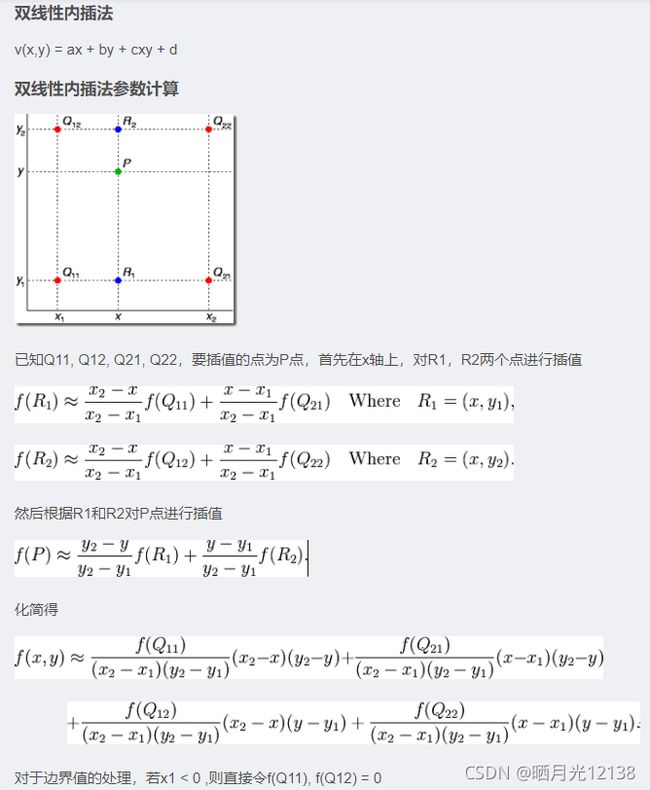
2.双线性内插法估计像素值:
在光流法的示例代码里有一段很奇怪的代码,一个内联函数:
//双线性内插法估计像素
inline float GetPixelValue(const cv::Mat &img, float x, float y) {
// 防止越界
if (x < 0) x = 0;
if (y < 0) y = 0;
if (x >= img.cols) x = img.cols - 1;
if (y >= img.rows) y = img.rows - 1;
//对x y取整,找到(x,y)为起点的指针
uchar *data = &img.data[int(y) * img.step + int(x)];
//xx yy为取整过程中忽略的小数部分
float xx = x - floor(x);
float yy = y - floor(y);
//双线性内插法估计像素
//data[0]就是(x,y)
//data[1]就是(x+1,y)
//data[img.step]就是(x,y+1)step是以字节为单位的矩阵有效宽度
//data[img.step + 1]就是(x+1,y+1)
return float(
(1 - xx) * (1 - yy) * data[0] +
xx * (1 - yy) * data[1] +
(1 - xx) * yy * data[img.step] +
xx * yy * data[img.step + 1]
);
}其实这里使用的是一个“双线性内插法估计像素”,主要是解决当优化过程中出现图像坐标不是整数的情况下像素值的计算,由于像素坐标必定是整数,如果直接向下取整误差较大,因此给出了一种对相邻的四个像素值加权的方法(找了一个现成的图,讲得非常清晰):
3.图像金字塔的使用
单层光流法:
void OpticalFlowTracker::calculateOpticalFlow(const Range &range) {
// parameters
// 窗口尺寸
int half_patch_size = 4;
// 迭代次数
int iterations = 10;
// 遍历每个关键点
for (size_t i = range.start; i < range.end; i++) {
//已知图像1的关键点坐标
auto kp = kp1[i];
//待估计的图像2中特征点相对图像1的特征点的x、y方向的变化
//注意:每个关键点对应的变化不同
double dx = 0, dy = 0; // dx,dy need to be estimated
//has_initial未初始化 默认值为false
if (has_initial) {
dx = kp2[i].pt.x - kp.pt.x;
dy = kp2[i].pt.y - kp.pt.y;
}
//代价函数、上一次代价函数值
double cost = 0, lastCost = 0;
//对当前点的光流匹配是否成功
bool succ = true;
// Gauss-Newton iterations
//Gauss-Newton法的H J b矩阵
Eigen::Matrix2d H = Eigen::Matrix2d::Zero(); // hessian
Eigen::Vector2d b = Eigen::Vector2d::Zero(); // bias
Eigen::Vector2d J; // jacobian
for (int iter = 0; iter < iterations; iter++) {
//inverse未初始化 默认值为false
if (inverse == false) {
H = Eigen::Matrix2d::Zero();
b = Eigen::Vector2d::Zero();
} else {
// only reset b
b = Eigen::Vector2d::Zero();
}
//重置代价函数值
cost = 0;
// 计算相关矩阵
//在关键点为中心的图像窗口内:
for (int x = -half_patch_size; x < half_patch_size; x++)
for (int y = -half_patch_size; y < half_patch_size; y++) {
//计算error:图像1关键点i的窗口-图像2待确定的对应关键点的窗口
double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -
GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy);;
//计算J矩阵:当前位置的图像反向梯度
if (inverse == false) {
J = -1.0 * Eigen::Vector2d(
0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
);
} else if (iter == 0) {
// in inverse mode, J keeps same for all iterations
// NOTE this J does not change when dx, dy is updated, so we can store it and only compute error
J = -1.0 * Eigen::Vector2d(
0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -
GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),
0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -
GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))
);
}
// 计算相关矩阵
b += -error * J;
cost += error * error;
if (inverse == false || iter == 0) {
// also update H
H += J * J.transpose();
}
}
// 计算增量
Eigen::Vector2d update = H.ldlt().solve(b);
// 匹配失败 没有对应合适的关键点
if (std::isnan(update[0])) {
// sometimes occurred when we have a black or white patch and H is irreversible
cout << "update is nan" << endl;
succ = false;
break;
}
//达到迭代次数或者代价函数未减小
if (iter > 0 && cost > lastCost) {
break;
}
// 更新变化值
dx += update[0];
dy += update[1];
lastCost = cost;
succ = true;
//更新量足够小时,停止迭代
if (update.norm() < 1e-2) {
// converge
break;
}
}
//记录成功匹配的标志位
success[i] = succ;
//记录匹配结果
kp2[i].pt = kp.pt + Point2f(dx, dy);
}
}多层光流法:
void OpticalFlowMultiLevel(
const Mat &img1,
const Mat &img2,
const vector &kp1,
vector &kp2,
vector &success,
bool inverse) {
// 图像金字塔层数
int pyramids = 4;
//倍率为0.5
double pyramid_scale = 0.5;
//得到每层的缩放倍率
double scales[] = {1.0, 0.5, 0.25, 0.125};
//创建金字塔
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
//Mat向量表示金字塔
vector pyr1, pyr2;
for (int i = 0; i < pyramids; i++) {
if (i == 0) {
//第0层最大 为原图
pyr1.push_back(img1);
pyr2.push_back(img2);
} else {
//resize图像 得到1 2 3层
Mat img1_pyr, img2_pyr;
cv::resize(pyr1[i - 1], img1_pyr,
cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
cv::resize(pyr2[i - 1], img2_pyr,
cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
pyr1.push_back(img1_pyr);
pyr2.push_back(img2_pyr);
}
}
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
auto time_used = chrono::duration_cast>(t2 - t1);
cout << "build pyramid time: " << time_used.count() << endl;
// coarse-to-fine LK tracking in pyramids
//由于是从最顶层开始 先计算顶层的图像1的关键点,直接按比例缩小
vector kp1_pyr, kp2_pyr;
for (auto &kp:kp1) {
auto kp_top = kp;
kp_top.pt *= scales[pyramids - 1];
kp1_pyr.push_back(kp_top);
kp2_pyr.push_back(kp_top);
}
//从高到低
for (int level = pyramids - 1; level >= 0; level--) {
// from coarse to fine
success.clear();
t1 = chrono::steady_clock::now();
//对当前层的两个图像进行单层的光流匹配
OpticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, success, inverse, true);
t2 = chrono::steady_clock::now();
auto time_used = chrono::duration_cast>(t2 - t1);
cout << "track pyr " << level << " cost time: " << time_used.count() << endl;
//放大到下一层作为初始值
if (level > 0) {
for (auto &kp: kp1_pyr)
kp.pt /= pyramid_scale;
for (auto &kp: kp2_pyr)
kp.pt /= pyramid_scale;
}
}
//记录最终结果
for (auto &kp: kp2_pyr)
kp2.push_back(kp);
}