AlphaFold2源码解析(9)--模型之损失及其他

AlphaFold2源码解析(9)–模型之损失及其他

损失函数和辅助头 该网络是端到端训练的，梯度来自主帧对齐点误差 (FAPE) 损失 $L_{FAPE}$和许多辅助损失。 每个示例的总损失可以定义如下

其中$L_{aux}$是结构模块的辅助损失（中间结构的平均 FAPE 和扭转损失，定义在算法 20 第 23 行），$L_{dist}$是分布图预测的平均交叉熵损失，$L_{msa}$是屏蔽 MSA 预测平均交叉熵损失，$L_{conf}$是 1.9.6 小节中定义的模型置信度损失，$L_{exp}$解析是 1.9.10 小节中定义的“实验解决”损失， $L_{viol}$是 1.9.11 小节中定义的违规损失。 最后两个损失仅在微调期间使用。为了降低短序列的相对重要性，我们将每个训练示例的最终损失乘以裁剪后残基数的平方根。 这意味着所有长于作物大小的蛋白质的权重相等，而较短的蛋白质则受到平方根惩罚。

FAPE、辅助、直方图和 MSA 损失的目的是将单独的损失附加到模型的每个主要子组件（包括配对和 MSA 最终嵌入）作为训练每个单元的“目的”指南. FAPE 和 aux 是 Structure 模块的直接结构术语。直方图损失确保Pair表示中的所有条目与相关的 $ij$ 残基对具有明确的关系，并确保配Pair表示对结构模块有用（消融显示这只是一个很小的影响）。直方图也是一种分布预测，因此它是我们解释模型在域间交互中的置信度的一种方法。 MSA 损失旨在迫使网络考虑序列间或系统发育关系来完成 BERT 任务，我们打算以此作为一种方式来鼓励模型考虑类似协同进化的关系，而无需明确编码协方差统计（这是意图，但我们只观察到它提高模型准确性的结果）。非常小的置信度损失允许构建 pLDDT 值而不会影响结构本身的准确性——我们之前在训练后微调了这个损失，但从一开始就以小的损失进行训练同样准确。最后，“违规”损失会促使模型生成具有正确键几何形状并避免冲突的物理上合理的结构，即使在模型高度不确定结构的情况下也是如此。这可以避免在最终的 AMBER 松弛中出现罕见的故障或精度损失。在训练早期使用违规损失会导致最终准确度略有下降，因为模型过度优化以避免冲突，因此我们只在微调期间使用它。

各种损失权重是手动选择的，并且仅在 AlphaFold 开发过程中略微调整（通常在引入损失项时尝试每个损失系数的几个值，之后很少调整权重）。 我们在模型开发的早期对 FAPE、直方图和 MSA 损失的比率进行了一些调整，但在模型开发过程中并没有重新调整太多。 对这些权重进行自动化或更广泛的调整可能会提高准确性，但我们通常没有观察到对激励我们这样做的精确值的强烈敏感性。 下面我们提供了应用于 Evoformer 输出表示以获得辅助预测的单个损失和转换的详细信息。

def loss(module, head_config, ret, name, filter_ret=True):
  if filter_ret:
    value = ret[name]
  else:
    value = ret
  loss_output = module.loss(value, batch)
  ret[name].update(loss_output)
  loss = head_config.weight * ret[name]['loss']
  return loss
for name, (head_config, module) in heads.items():
     ......
	total_loss += loss(module, head_config, ret, name)

侧链和主链扭转角损失

预测的侧链扭转角和骨架扭转角用单位圆上的点表示，即 ${\hat{a}}_i^f\in R^2$ 且$||{\hat{a}}_i^f||=1$ ，将它们以$R^2$中$L2$损失与真实扭转角$a_i^{true,f}$进行比较。它在数学上等价于夹角差的余弦。

一些侧链部分是180旋转对称的，因此预测的扭转角$\chi$和$\chi +\pi$得到相同的物理结构。我们允许网络产生任意一个扭转角通过提供另一个角度${\alpha }_i^{alttruth,f}={\alpha }_i^{true,f}+\pi$, 对于所有的非对称构型，我们设${\alpha }_i^{alttruth,f}={\alpha }^{true,f}$。

引入了一个小的辅助损失$L_{anglenorm}$ ，使预测点靠近单位圆。 这有两个原因：一是避免向量太靠近原点，这会导致数值不稳定的梯度。 另一个是虽然向量的范数不影响输出，但它确实影响网络的学习动力。 当查看梯度在归一化的反向传递中如何变换时，梯度将被非归一化向量的范数重新缩放。

由于模型是高度非线性的，这些向量的长度可以在训练过程中发生强烈变化，导致不期望的学习动态。加权因子是在特定的基础上选择的，测试了几个值，并选择最小的一个，使向量的范数保持稳定。在模型性能方面，我们没有观察到任何对精确值的强烈依赖。

两个角(α和β)用L2范数比较表示为单位圆上的点，在数学上等价于角差的余弦

第一个恒等式就是普通的余弦差公式。

def supervised_chi_loss(ret, batch, value, config):
  """Computes loss for direct chi angle supervision.

  Jumper et al. (2021) Suppl. Alg. 27 "torsionAngleLoss"

  Args:
    ret: Dictionary to write outputs into, needs to contain 'loss'.
    batch: Batch, needs to contain 'seq_mask', 'chi_mask', 'chi_angles'.
    value: Dictionary containing structure module output, needs to contain
      value['sidechains']['angles_sin_cos'] for angles and
      value['sidechains']['unnormalized_angles_sin_cos'] for unnormalized
      angles.
    config: Configuration of loss, should contain 'chi_weight' and
      'angle_norm_weight', 'angle_norm_weight' scales angle norm term,
      'chi_weight' scales torsion term.
  """
  eps = 1e-6

  sequence_mask = batch['seq_mask']
  num_res = sequence_mask.shape[0]
  chi_mask = batch['chi_mask'].astype(jnp.float32)
  pred_angles = jnp.reshape(
      value['sidechains']['angles_sin_cos'], [-1, num_res, 7, 2])
  pred_angles = pred_angles[:, :, 3:]

  residue_type_one_hot = jax.nn.one_hot(
      batch['aatype'], residue_constants.restype_num + 1,
      dtype=jnp.float32)[None]
  chi_pi_periodic = jnp.einsum('ijk, kl->ijl', residue_type_one_hot,
                               jnp.asarray(residue_constants.chi_pi_periodic))

  true_chi = batch['chi_angles'][None]
  sin_true_chi = jnp.sin(true_chi)
  cos_true_chi = jnp.cos(true_chi)
  sin_cos_true_chi = jnp.stack([sin_true_chi, cos_true_chi], axis=-1)

  # This is -1 if chi is pi-periodic and +1 if it's 2pi-periodic
  shifted_mask = (1 - 2 * chi_pi_periodic)[..., None]
  sin_cos_true_chi_shifted = shifted_mask * sin_cos_true_chi

  sq_chi_error = jnp.sum(
      squared_difference(sin_cos_true_chi, pred_angles), -1)
  sq_chi_error_shifted = jnp.sum(
      squared_difference(sin_cos_true_chi_shifted, pred_angles), -1)
  sq_chi_error = jnp.minimum(sq_chi_error, sq_chi_error_shifted)

  sq_chi_loss = utils.mask_mean(mask=chi_mask[None], value=sq_chi_error)
  ret['chi_loss'] = sq_chi_loss
  ret['loss'] += config.chi_weight * sq_chi_loss
  unnormed_angles = jnp.reshape(
      value['sidechains']['unnormalized_angles_sin_cos'], [-1, num_res, 7, 2])
  angle_norm = jnp.sqrt(jnp.sum(jnp.square(unnormed_angles), axis=-1) + eps)
  norm_error = jnp.abs(angle_norm - 1.)
  angle_norm_loss = utils.mask_mean(mask=sequence_mask[None, :, None],
                                    value=norm_error)

  ret['angle_norm_loss'] = angle_norm_loss
  ret['loss'] += config.angle_norm_weight * angle_norm_loss

帧对齐点错误（FAPE）

帧对齐点误差(Frame Aligned Point Error, FAPE)对一组预测局部帧$\{T_i\}$下的一组预测原子坐标$\{x_j\}$与对应的地面真值原子坐标$x_j^{true}$和真值局部帧$\{T_i^{true}\}$进行评分。最终的FAPE损失对所有主链和侧链框架中的所有原子进行评分。此外，在结构模块的每一层中使用一个更便宜的版本作为辅助损耗。

为了表述损失，我们计算了相对于坐标系$T_i$的原子位置$x_j$和相应的真原子位置$x_j^{true}$相对于真坐标系$T_i^{true}$的位置。偏差计算为稳健的L2范数。($ϵ$是一个添加的小常数，以确保梯度在数值上表现良好。这个常数的确切值并不重要，只要它足够小。我们在实验中使用了$10^4$和$10^{12}$的值)。由此产生的$N_{frames}\times N_{atoms}$偏差用长度刻度$Z=10\mathring{A}$的l1损失进行惩罚，以使损失无单位。

在本节中，我们表示Å中的点位置和超参数，尽管损失对单位的选择是不变的。

我们现在讨论在真实结构和预测结构的整体刚性变换下损失的行为。首先，我们应该注意到$x_{ij}$在刚性运动(不包括反射)下是不变的;因此，如果通过任意旋转和平移，预测结构与真实值不同，损失将保持不变。然而，由于局部框架的构造方式，由于局部框架的z轴转换为伪向量，因此在反射下损失不是不变的。这意味着从结构构建框架的方式不受我们所做的精确选择的限制，但只要它们在预测结构和目标结构之间以一致的方式构建，就可以有所不同。

def frame_aligned_point_error(
    pred_frames: r3.Rigids,  # shape (num_frames)
    target_frames: r3.Rigids,  # shape (num_frames)
    frames_mask: jnp.ndarray,  # shape (num_frames)
    pred_positions: r3.Vecs,  # shape (num_positions)
    target_positions: r3.Vecs,  # shape (num_positions)
    positions_mask: jnp.ndarray,  # shape (num_positions)
    length_scale: float,
    l1_clamp_distance: Optional[float] = None,
    epsilon=1e-4) -> jnp.ndarray:  # shape ()
  
  assert pred_frames.rot.xx.ndim == 1
  assert target_frames.rot.xx.ndim == 1
  assert frames_mask.ndim == 1, frames_mask.ndim
  assert pred_positions.x.ndim == 1
  assert target_positions.x.ndim == 1
  assert positions_mask.ndim == 1

  # Compute array of predicted positions in the predicted frames.
  # r3.Vecs (num_frames, num_positions)
  local_pred_pos = r3.rigids_mul_vecs(
      jax.tree_map(lambda r: r[:, None], r3.invert_rigids(pred_frames)),
      jax.tree_map(lambda x: x[None, :], pred_positions))

  # Compute array of target positions in the target frames.
  # r3.Vecs (num_frames, num_positions)
  local_target_pos = r3.rigids_mul_vecs(
      jax.tree_map(lambda r: r[:, None], r3.invert_rigids(target_frames)),
      jax.tree_map(lambda x: x[None, :], target_positions))

  # Compute errors between the structures.
  # jnp.ndarray (num_frames, num_positions)
  error_dist = jnp.sqrt(
      r3.vecs_squared_distance(local_pred_pos, local_target_pos)
      + epsilon)

  if l1_clamp_distance:
    error_dist = jnp.clip(error_dist, 0, l1_clamp_distance)

  normed_error = error_dist / length_scale
  normed_error *= jnp.expand_dims(frames_mask, axis=-1)
  normed_error *= jnp.expand_dims(positions_mask, axis=-2)

  normalization_factor = (
      jnp.sum(frames_mask, axis=-1) *
      jnp.sum(positions_mask, axis=-1))
  return (jnp.sum(normed_error, axis=(-2, -1)) /
          (epsilon + normalization_factor))

AlphaFold 的手性特性及其损失

在本节中，我们将详细查看全局反射下各个组件的变换属性

在这种全局反射下，帧的坐标也以非平凡的方式变化。简单的代数表明

其中旋转矩阵$R_i$的非平凡变换来自于算法21中的叉乘。旋转矩阵的非平凡变换也意味着局部点KaTeX parse error: Got function '\vec' with no arguments as argument to '\dot' at position 15: T^{-1}_i \dot \̲v̲e̲c̲{x}_j在反射下不是不变的。全局反射的作用是只反射局部坐标KaTeX parse error: Got function '\vec' with no arguments as argument to '\dot' at position 15: T^{-1}_i \dot \̲v̲e̲c̲{x}_j的z分量。

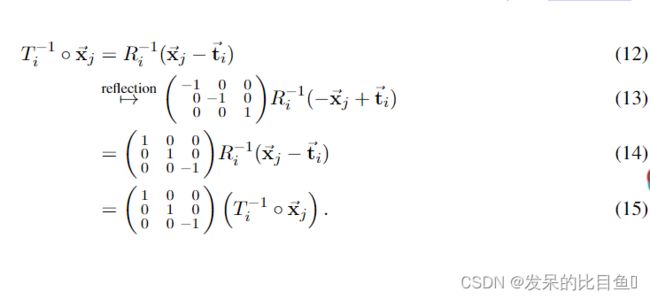
在下面，我们用大罗马字母表示一组框架和点，例如$X=(\{x_i\},\{T_j\})$
特别地，这意味着FAPE和IPA都可以区分蛋白质的全局反射，假设刚性帧与算法21的底层点相关，例如

这在退化情况之外是一个很大的正值。对于FAPE可以区分手性的更一般的证明，而不管框架是如何构造的，请参阅下一节

AlphaFold中还有其他手性来源。原子位置是根据主骨架和预测的χ角组合计算的，这个过程总是会生成一个左手分子，因为它使用了χ角之外的理想值(即CB总是在左手位置)。AlphaFold几乎可以完全生成主链原子的手性对，但它不能构建侧链的手性对。该模型对χ角值的损失较小，且这些值在反射下不是不变的。

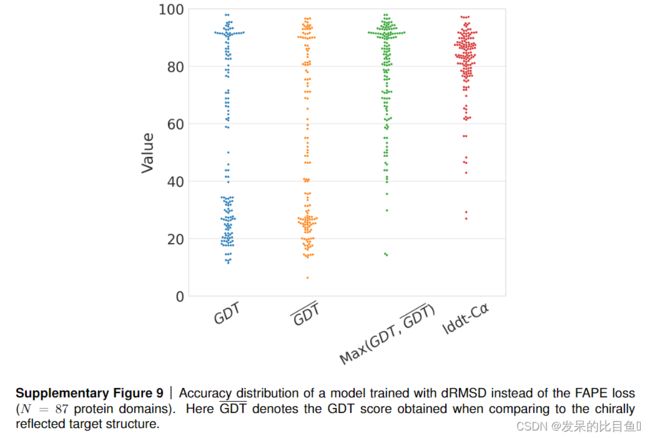
为了测试FAPE手性的重要性，我们使用dRMSD损失代替FAPE训练了一个模型，我们在图9中显示了CASP14集上的结果。这里我们可以看到lDDT-Cα的性能仍然很好，我们注意到lDDT-Cα是一个不能区分相反手性分子的规则。

然而，如果用dRMSD损失进行训练，GDT显示出双峰分布，其中两种模式之一仅比基线AlphaFold略差，而另一种模式具有非常低的精度(Suppl。图9)。这表明第二模式是由反手性分子组成的。为了测试这一点，我们计算了GDT，这是用于计算GDT的结构的镜面反射的GDT。这些镜像结构也显示了GDT值的双峰性。最后，取结构和其镜像的GDT的最大值产生一致的高GDT。这证实了使用dRMSD损耗训练的AlphaFold经常产生镜像结构，而FAPE是确保预测结构正确手性的主要组成部分。

FAPE(X,Y) = 0 的配置

为了理解实现零FAPE损失的点，我们将引入一个类似rmsd的辅助度量，它只对点而不是帧起作用

$T$是恰当的刚性变换。然后，我们可以显示FAPE的下界，而不考虑帧的值

因为S函数在所有固有刚变换中使括号内的量最小化$T_i{T}_i^{-1}$是一个固有刚变换。这个不等式简单地表明，在相同的距离函数下，所有局部帧的平均点误差不小于最佳单全局对齐的点误差。

如果KaTeX parse error: Expected 'EOF', got '}' at position 39: …at{\vec{x}}_i\}}̲) = 0，则值KaTeX parse error: Expected 'EOF', got '}' at position 36: …at{\vec{x}}_i\}}̲)为零，这表明只有当KaTeX parse error: Expected 'EOF', got '}' at position 39: …at{\vec{y}}_i\}}̲) = 0时，$FAPE(X,X)=0$才有可能。我们可以将$FAPE(X,X)=0$的所有对描述为RMSD = 0且T是实现零KaTeX parse error: Expected 'EOF', got '}' at position 39: …at{\vec{y}}_i\}}̲) = 0的刚性运动之一。 特别是，如果点集是非简并的，FAPE损失总是具有非零值手性对，而不管框架是如何构造的。

FAPE 的度量属性

模型置信度预测（pLDDT）

TM-score 预测

直方图预测

屏蔽 MSA 预测

实验解决”预测

结构违规