经典卷积神经网络-LeNet(pytorch实现)
目录
一、LeNet的基础概念
二、LeNet模型介绍
1.LeNet的基础模型介绍
2.LeNet的八层模型预览
3.卷积计算
4.LeNet模型的详细介绍
三、LeNet-5 代码实现
一、LeNet的基础概念
LeNet-5出自论文Gradient-Based Learning Applied to Document Recognition,是一种用于手写体字符识别的非常高效的卷积神经网络。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。如今各大深度学习框架中所使用的LeNet都是简化改进过的LeNet-5(-5表示具有5个层),和原始的LeNet有些许不同,比如把激活函数改为了现在很常用的ReLu。
二、LeNet模型介绍
1.LeNet的基础模型介绍
LeNet分为卷积层块和全连接层块两个部分。
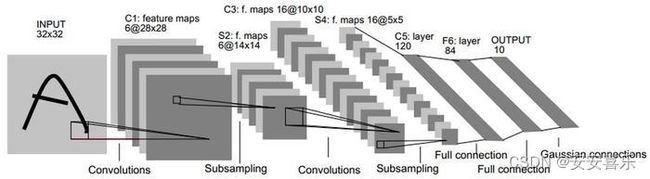
LeNet-5识别手写体数字的过程,其包含输入层在内共有八层,每一层都包含多个参数(权重),C层代表的为卷积层,通过卷积操作,使原信号特征增强,并降低噪音。S层代表下采样层,即池化层,利用图像局部相关性的原理,对图像进行了子抽样,可以减少数据处理量,同时也可以保留一定的有用信息。
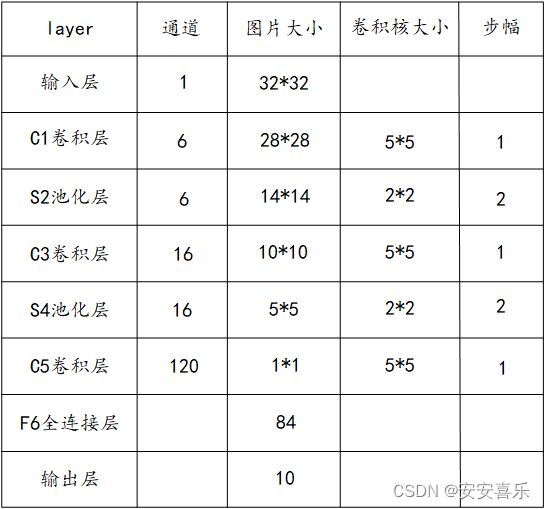
2.LeNet的八层模型预览
第一层:输入层;单通道的32*32大小的图像
第二层:C1卷积层
第三层:S2池化层(下采样层)
第四层:C3卷积层
第五层:S4池化层(下采样层)
第六层:C5卷积层
第七层:F6全连接层
第八层:输出层,输出长度为10的张量
3.卷积计算
(1)目的:
卷积运算的目的是提取输入的不同特征,某些卷积层的可能只能提取一些低级的特征,更多层的 网络能从低级特征中迭代提取更复杂的特征。
(2)参数:
size:卷积核/过滤器的大小;通常选择3*3、5*5;
padding:在输入高和宽的两侧填充元素(通常是0元素),可以用来增加输出的高和宽,使输入 与输出具有相同的宽和高;
stride:步幅,默认为1。步幅可以减小高和宽。
(3)计算公式:
假设图片输入的形状是![]() ,卷积核窗口形状是
,卷积核窗口形状是![]() ,那么输出的形状将会是:
,那么输出的形状将会是:
![]() ,卷积层的输出形状由输入形状和卷积窗口形状决定;
,卷积层的输出形状由输入形状和卷积窗口形状决定;
如果在高的两侧一共填充了![]() 行,在宽的两侧一共填充了
行,在宽的两侧一共填充了![]() 列,那么输出的形状将会是:(nh-
列,那么输出的形状将会是:(nh-![]() ,输出的高和宽会分别增加
,输出的高和宽会分别增加![]()
![]()
如果在高上的步幅为![]() ,宽上的步幅为
,宽上的步幅为![]() ,那么输出的形状将会是:
,那么输出的形状将会是:![]()
(4)通道
通道(Channel)也叫做特征图(Feature Map)。卷积网络中主要有两个操作:卷积(Convolution),池化(Pooling)。池化层并不会对通道之间的交 互有影响,只是在各个通道中进行操作;而卷积层则可以在通道与通道之间进行交互,之后在下 一层生成新的通道。
4.LeNet模型的详细介绍
第一层 输入层
输入层,输入图像的大小为32*32,这要比mnist数据库中的最大字母(28*28)还大,这样做的目的是希望潜在的明显特征,比如笔画断续,角点等能够出现在最高层特征监测子感受野的中心。
第二层 C1卷积层
(1)特征图大小:使用 6 个尺寸为 5 × 5 的卷积核,在卷积的过程中不做边缘填充,步长
为 stride=1 。单个核的卷积输出大小为 (32−5+1) × (32−5+1)=28 × 28 。由于有 6 个卷积核,
所以整个卷积层输出得到为 Feature Map 为 28 × 28 × 6 。
(2)参数个数:由于参数(权值)共享的原因,对于同个卷积核每个神经元均使用相同
的参数,因此,参数个数为(5× 5+1 )× 6= 156 ,其中 5 × 5 为卷积核参数, 1 为偏置参数。
(3)连接数: (5 × 5+1) × 28 × 28 × 6=122304 。在卷积层,每个输出的 28 × 28 的
Feature Map ,都和一个 5 × 5 卷积核相连。每个卷积核都有一个偏置。
第三层 S2池化层
(1)特征图大小:池化单元为 2 × 2 ,池化单元之间没有重叠,在池化区域内进行聚合统
计后得到新的特征值,因此经 2 × 2 池化后,每两行两列重新算出一个特征值出来,相当
于图像大小减半,因此卷积后的 28 × 28 图像经 2 × 2 池化后就变为 14 × 14 。这一层的计算
过程是: 2 × 2 单元里的值相加,然后再乘以训练参数 w ,再加上一个偏置参数 b (每一个
特征图共享相同的 w 和 b) ,然后取 sigmoid 值( S 函数: 0-1 区间),作为对应的该单元的
值
(2)参数个数: S2 层由于每个特征图都共享相同的 w 和 b 这两个参数,因此需要 2 × 6=12
个参数。
(3)连接数:下采样之后的图像大小为 14 × 14 ,因此 S2 层的每个特征图有 14 × 14 个神
经元,每个池化单元连接数为 2 × 2+1 ( 1 为偏置量),因此,该层的连接数为(2× 2+1) ×14 × 14 × 6 = 5880
第四层 C3卷积层
(1)特征图大小: C3 层有 16 个特征图, 60 个卷积核,卷积模板大小为 5 × 5 。与 C1 层的
分析类似, C3 层的特征图大小为( 14-5+1 )×( 14-5+1 ) = 10 × 10 。
(2)参数个数: C3 与 S2 并不是全连接而是部分连接,有些是 C3 连接到 S2 三层、有些四
层、甚至达到 6 层。一是可以减少连接个数,二是打破网络的对称结构,提取不同特征。
计算过程为:用 3 个卷积模板分别与 S2 层的 3 个 feature maps 进行卷积,然后将卷积的结
果相加求和,再加上一个偏置,再取 sigmoid 得出卷积后对应的 feature map 了。参数:
(5× 5 × 3+1 )× 6 + (5× 5 × 4+1 )× 9 + (5× 5 × 6+1 ) = 1516
(3)连接数:卷积后的特征图大小为 10 × 10 ,参数数量为 1516 ,因此连接数为
1516 × 10 × 10= 151600
第五层 S4 池化层
(1)特征图大小:与 S2 的分析类似,池化单元大小为 2 × 2 ,因此,该层与 C3 一样共有
16 个特征图,每个特征图的大小为 5 × 5 。
( 2 )参数个数:与 S2 的计算类似,所需要参数个数为 16 × 2 = 32
( 3 )连接数:连接数为(2× 2+1 )× 5 × 5 × 16 = 2000
第六层 C5卷积层
(1)特征图大小:该层有 120 个特征图,每个卷积核的大小为 5 × 5 ,因此有 120 个特征图。C5 的每个特征图与 S4 的 16 个特征图全部相连。特征图大小为(5-5+1)×(5-5+1) = 1× 1
(2)参数个数:本层的参数数目为 120 ×(5× 5 × 16+1 ) = 48120
(3)连接数:由于该层的特征图大小刚好为 1 × 1 ,因此连接数为 48120 × 1 × 1=48120
注意:该层刚好变成了全连接,这只是巧合,如果原始输入的图像比较大,则该层就不是
全连接了。所以依然称为卷积层.
第七层 F6全连接层
(1)特征图大小: F6 层有 84 个单元,之所以选这个数字的原因是来自于输出层的设计,
对应于一个 7 × 12 的比特图。 0 表示白色, 1 表示黑色,这样每个符号的比特图的黑白色就
对应于一个编码。该层有 84 个特征图,特征图大小与 C5 一样都是 1 × 1 ,与 C5 层全连接。
(2)参数个数:由于是全连接,参数数量为( 120+1 )× 84=10164
(3)连接数:由于是全连接,连接数与参数数量一样,也是 10164
第八层 输出层
(1)特征图大小: Output 层也是全连接层,共有 10 个节点,分别代表数字 0 到 9 。如果第 i
个节点的值为 0 ,则表示网络识别的结果是数字 i 。
(2)参数个数:由于是全连接,参数个数为 84 × 10=840
(3)连接数:由于是全连接,连接数与参数个数一样,也是 840
三.LeNet-5 代码实现
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
import torchvision
import torchvision.transforms as transforms
import time
import matplotlib.pyplot as plt
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
# 导入FashionMNIST数据集
mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
# 处理数据集,把数据转换成张量,使数据可以输入下面我们搭建的网络
def load_data_fashion_mnist(mnist_train, mnist_test, batch_size):
if sys.platform.startswith('win'):
num_workers = 0
else:
num_workers = 4
train_data = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_data = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
return train_data, test_data
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5), # in_channels, out_channels, kernel_size
nn.LeakyReLU(0.1),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
nn.LeakyReLU(0.1),
nn.MaxPool2d(2, 2)
)
self.fc = nn.Sequential(
nn.Linear(16*4*4, 120),
nn.LeakyReLU(0.1),
nn.Linear(120, 84),
nn.ReLU(),
nn.Linear(84, 10)
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output
# 测试准确率计算
def evaluate_accuracy(data_iter, net, device=None):
if device is None and isinstance(net, torch.nn.Module):
# 如果没指定device就使用net的device
device = list(net.parameters())[0].device
acc_sum, n = 0.0, 0
with torch.no_grad():
for X, y in data_iter:
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() # 改回训练模式
n += y.shape[0]
return acc_sum / n
# 训练函数
def train(net, train_data, test_data, batch_size, optimizer, device, num_epochs):
net = net.to(device)
print("training on ", device)
loss_function = torch.nn.CrossEntropyLoss() # 定义损失函数(交叉熵损失函数)
ax = [] # 保存等会更新的epoch,loss,train_acc,test_acc,用于绘制动态折线图
ay1 = []
ay2 = []
ay3 = []
plt.ion()
# 开始训练
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n, batch_count, start = 0.0, 0.0, 0, 0, time.time() # 初始化参数
for X, y in train_data:
X = X.to(device) # 把参数导入GPU训练
y = y.to(device)
y_hat = net(X)
l = loss_function(y_hat, y) # 使用损失函数计算loss
optimizer.zero_grad()
l.backward() # 反向传播
optimizer.step()
train_l_sum += l.cpu().item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
n += y.shape[0]
batch_count += 1
test_acc = evaluate_accuracy(test_data, net) # 测试当个epoch的训练的网络
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
% (epoch + 1, train_l_sum / batch_count, train_acc_sum / n, test_acc, time.time() - start))
# 绘制动态折线图(如果不想绘制,可以删掉)
plt.clf() # 清除刷新前的图表,防止数据量过大消耗内存
ax.append(epoch + 1) # 追加x坐标值
ay1.append(train_l_sum / batch_count) # 追加y坐标值
ay2.append(train_acc_sum / n)
ay3.append(test_acc)
plt.plot(ax, ay1, 'g-')
plt.plot(ax, ay2, 'r-')
plt.plot(ax, ay3, '-')
plt.ylabel("epoch")
plt.plot(ax, ay1, label="loss") # 在绘图函数添加一个属性label
plt.plot(ax, ay2, label="train_acc")
plt.plot(ax, ay3, label="test_acc")
plt.legend(loc=2) # 添加图例,loc为图例位置,1为右上角,2为左上角,3为左下角,4为右下角
plt.grid() # 添加网格
plt.pause(5) # 设置暂停时间,太快图表无法正常显示
plt.ioff() # 关闭画图的窗口,即关闭交互模式
plt.show() # 显示图片,防止闪退
if __name__ == '__main__':
batch_size = 256 # 批量数大小
train_data, test_data = load_data_fashion_mnist(mnist_train, mnist_test, batch_size)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 使用GPU,如果没有则使用CPU
net = LeNet() # 导入我们搭建好的网络
lr, num_epochs = 0.001, 10
optimizer = torch.optim.Adam(net.parameters(), lr=lr) # 优化函数
train(net, train_data, test_data, batch_size, optimizer, device, num_epochs)