数据结构--图

图

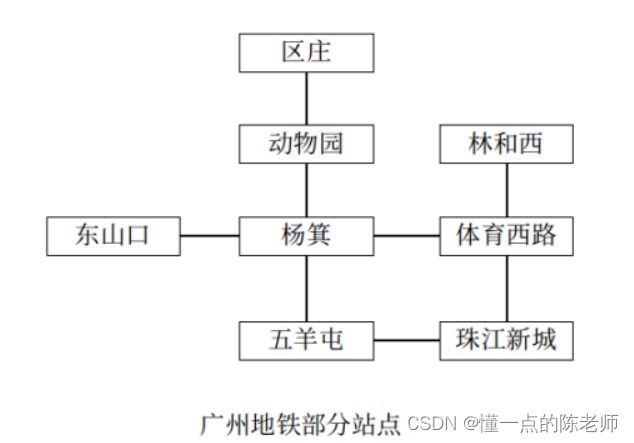
常见图结构：

和树结构有什么不一样？

看到图结构关系比树复杂，而且没有层级概念，是一种多对多关系，那么在算法中，要怎样去表达这种结构关系呢？

定义

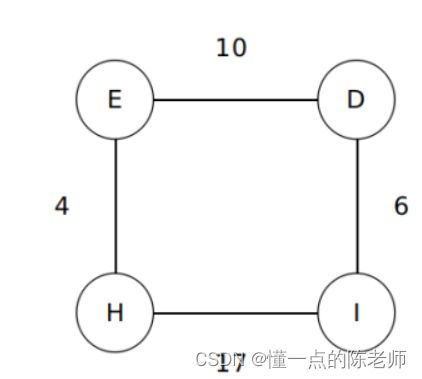
在计算机科学中，一个图（Graph）就是一些顶点（Vertex）的集合，这些顶点通过一系列的边（Edge）连接。顶点一般用圆圈表示，边就是这些圆圈之间的连线，顶点之间通过边连接。如上图，顶点包括｛东山口，区庄，动物园，杨箕，五羊屯，林和西，体育西路，珠江新城｝，边就是链接顶点的线，但我们知道不是每个站点相间的距离都一样，例如从东山口到杨箕是3公里，从杨箕到五羊屯是5公里，这样我们再引入一个概念称为权重（Weight），如图：

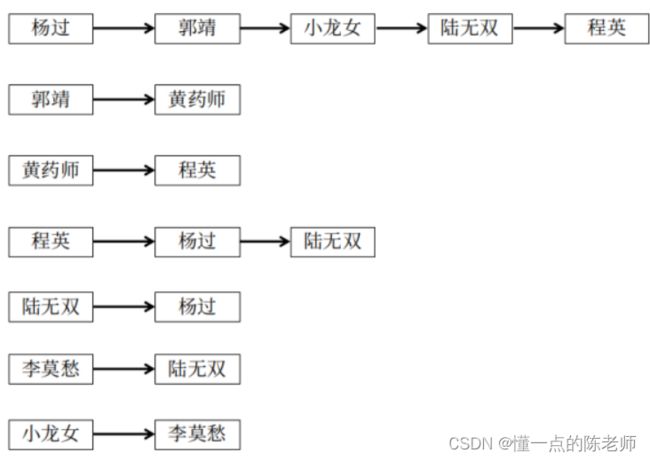
然后我们再看一下图，边变成带箭头的线，表示一种单方面的关系。我们可以这样理解，杨过的伯伯是郭靖，杨过的姑姑是小龙女，但我们反过来就不能称小龙女的姑姑是杨过。

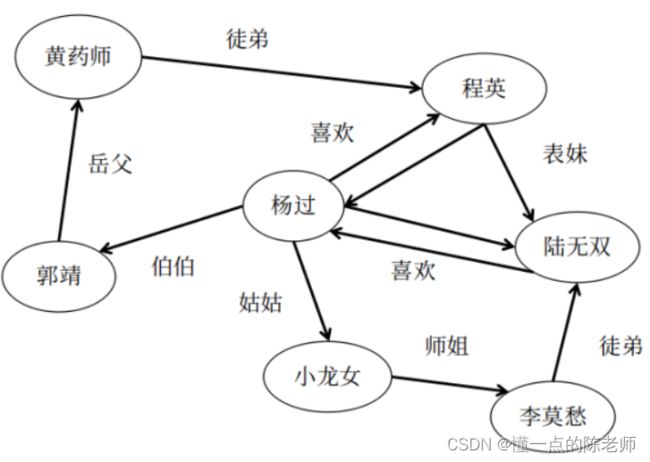
所以一般有这几种类型的图。

1. 无权无向图。
2. 无权有向图。
3. 有权无向图。
4. 有权有向图。

可以通过这个连接，动态观察图的表示

图的表示

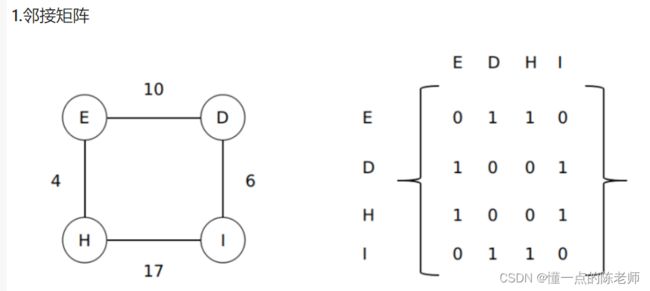
1.邻接矩阵

2. 邻接列表

两种结构的优缺点

操作	邻接列表	邻接矩阵
存储空间	O(V+E)	O(V^2)
增加顶点	O(1)	O(V^2)
增加边	O(1)	O(1)
检查顶点相邻性	O(V)	O(1)

邻接矩阵代码表示

E,D,H,I = range(4)
adjacency_matrix =[
    [0, 1, 1, 0],
    [1, 0, 0, 1],
    [1, 0, 0, 1],
    [0, 1, 1, 0]]
# 邻接矩阵可以直观判断两个顶点是否关联
print("E和D关联" if adjacency_matrix[E][D] else "E和D不关联" )
print("E和I关联" if adjacency_matrix[E][I] else "E和I不关联" )


# 如果要把权重带上，可以在邻接矩阵上把1替换成权重，创建有权无向图邻接矩阵
adjacency_matrix_2 =[
    [0, 10, 4, 0],
    [10, 0, 0, 6],
    [4, 0, 0, 17],
    [0, 6, 17, 0]]
print("E-D:", adjacency_matrix_2[E][D])  # E-D: 10

邻接列表

adjacency_list = {
  '杨过':{'郭靖':'伯伯', '小龙女':'姑姑', '陆无双':'喜欢', '程英':'喜欢'},
  '郭靖':{'黄药师':'岳父'},
  '黄药师':{'程英':'徒弟'},
  '程英':{'杨过':'喜欢','陆无双':'表妹'},
  '陆无双':{'杨过':'喜欢'},
  '李莫愁':{'陆无双':'徒弟'},
  '小龙女':{'李莫愁':'师姐'},
}
print("郭靖是杨过的%s" % adjacency_list['杨过']['郭靖'])
print("黄药师是郭靖的%s" % adjacency_list['郭靖']['黄药师'])

得益于Python的字典（dict）数据类型，在字典里面嵌套字典便能表现有权图的邻接列表。如果是无权图可以用字典嵌套集合（set）来展现。

graph = {'A': set(['B', 'C']),
          'B': set(['A', 'D', 'E']),
          'C': set(['A', 'F']),
          'D': set(['B']),
          'E': set(['B', 'F']),
          'F': set(['C', 'E'])}

图的遍历

动态演示遍历算法

深度优先搜索法（DFS）：

根据字面意思，就是顺着起始顶点访问一个没有访问过的顶点，一直走到没有新的顶点可以访问的时候，才往后退回上一个顶点，看一下有没有新的顶点可以访问，如果有又继续深入，直到所有顶点都被访问。

广度优先搜索法（BFS）：

从一个顶点出发，把它所有关联的顶点依次访问，然后到下一个顶点（刚才访问的关联顶点）。然后以这个顶点为中心，再次访问所有关联顶点，直到所有顶点被访问。

完整代码演示

# 创建有无有向图的邻接列表
graph = {'A': ['B', 'C'],
         'B': ['A', 'D', 'E'],
         'C': ['A', 'F', 'G'],
         'D': ['B'],
         'E': ['B', 'F', 'G'],
         'F': ['C', 'E'],
         'G': ['C', 'E']}

def graph_dfs(adjacency_list, start_point):
    """图的深度优先搜索法"""
    visited = [start_point]      # 保存已经访问过的顶点
    stack = [[start_point, 0]]   # 用栈数据结构来记录访问历史，
    #result = [start_point]
    while stack: # 当栈为空，说明全部顶点已经遍历完成
        (current_point, next_point_index) = stack[-1]  # 获取当前访问的顶点
        if (current_point not in adjacency_list) or (next_point_index >= len(adjacency_list[current_point])):
            stack.pop() # 当前顶点没有新的可以访问关联顶点，那么就出栈
            continue
        next_point = adjacency_list[current_point][next_point_index]
        stack[-1][1] += 1            # 记录当前访问的顶点的这个关联顶点已经被访问
        if next_point in visited:    # 若已经访问了，继续找下一个
            continue
        visited.append(next_point)   # 若是新的顶点，那就添加到已访问顶点
        stack.append([next_point, 0])# 新的顶点入栈　
    return visited  # 返回访问顶点的结果
#------------测试--------------------
res = graph_dfs(graph, 'A')
print("->".join(res))  # A->B->D->E->F->C->G

def graph_bfs(adjacency_list, start_point):
    visited = [start_point] # 保存已经访问过的顶点
    queue = []              # 用队列结构来记录访问历史
    queue.append(start_point)
    while len(queue) > 0:   # 当队列为空，说明全部顶点已经遍历完成
        current_point = queue.pop(0)  # 获取访问历史的队头为当前顶点
        for next_point in adjacency_list.get(current_point, []):
            # 逐一访问当前顶点的所有关联点
            if next_point not in visited:  
                visited.append(next_point)
                queue.append(next_point)   # 在队尾添加顶点作为访问记录
    return visited
#------------测试--------------------
res = graph_bfs(graph, 'A')
print("->".join(res)) # A->B->C->D->E->F->G