广度优先搜索以及C++实现
一、引入两个问题
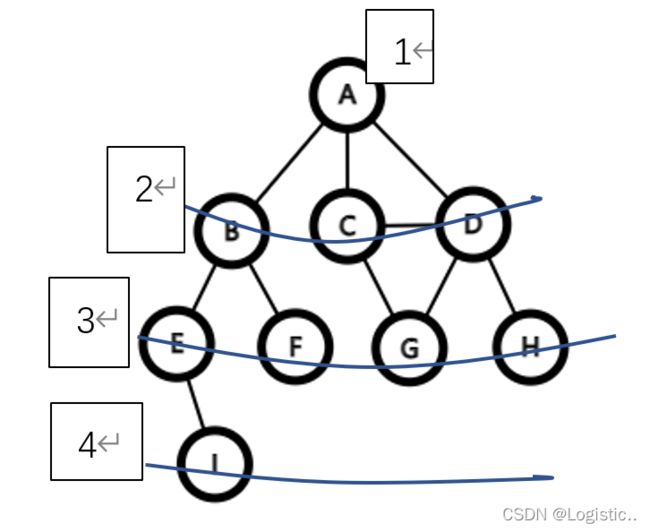
- 给出图1从任意一点开始的广度优先搜索遍历的序列，
（1）设置BFS返回值为向量的代码；
（2）设置BFS无返回值，同时点集用字符串表示，要求输出结果打印到屏幕上
图1
- 岛屿数量问题（类似于迷宫问题），来自leetcode200题。
给你一个由 '1'（陆地）和 '0'（水）组成的二维网格，请你计算网格中岛屿的数量。岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围
示例：
输入：grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出：3
二、首先介绍一下什么是广度优先搜索
1.先以实例来演示
（1）对图1来说，以A为源点进行广度优先搜索
图3
序列：A B C D E F G H I
（2）对图1来说，以B为源点进行广度优先搜索
图3
序列：B A E F C D I G H
2.操作方法
已知一个图的顶点集合为
顶点
的邻接点集合为
首先选定一个起始点
1)、访问顶点
2)、访问完 的所有未被访问的邻接点
3)、依次从这些邻接点
（在步骤2中访问的顶点）出发，访问它们的所有未被访问的邻接点; 依此类推，直到图中所有访问过的顶点的邻接点都被访问
可以发现，广度优先搜索类似于树的层次遍历
3.实现方法
广度优先搜索具体怎么实现
广度优先搜索主要用到队列这个数据结构，与之相似的深度优先搜索主要用到栈。
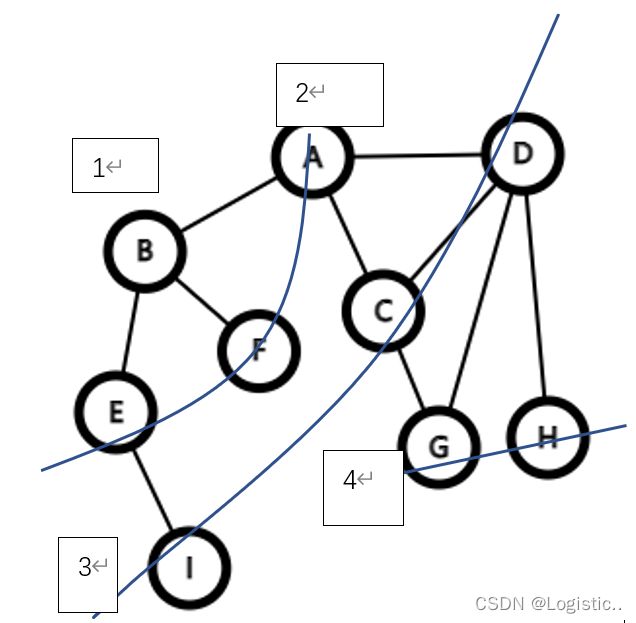
(1)以图2为例
设置两个队列，第一个队列que用来操作BFS，第二个队列Note用来记录边路序列
1).节点A进入队列que，标记已访问，A推入队列Note，已访问节点集合
2).A的所有未访问邻接点(B,C,D）进入队列que，标记已访问，A弹出队列, B，C，D推入队列Note，已访问节点集合
3).B的所有未访问邻接点(E,F)进入队列que，标记已访问，B弹出队列que，E，F推入队列Note, 已访问节点集合
4).C的所有未访问邻接点G进入队列que，标记已访问，C弹出队列que，G推入队列Note, 已访问节点集合
5).D的所有未访问邻接点H进入队列que，标记已访问，D弹出队列que，H推入队列Note, 已访问节点集合
6).E的所有未访问邻接点I进入队列que，标记已访问，E弹出队列que，I推入队列Note, 已访问节点集合
7).F没有未访问的邻接点,F弹出队列que,已访问节点集合
8).G没有未访问的邻接点,G弹出队列que,已访问节点集合
9).H没有未访问的邻接点,H弹出队列que,已访问节点集合
10).I没有未访问的邻接点,I弹出队列que,已访问节点集合
(2)算法具体化
已知一个图的顶点集合为
顶点的邻接点集合为
已访问的节点集合为
这里
分别是
个取值为1~n的自然数
首先选定一个起始点
1、访问顶点 ，顶点推入队列，加入集合
.
2、访问完队头元素() 的所有未被访问的邻接点
，并把诸
推入队列，放入集合，再把队头元素弹出队列
3、再次访问队头元素
（在步骤2中访问的节点的第一个邻接点），访问它的所有未被访问的邻接点，把所有访问到的邻接点推入队列，放入集合，弹出队头元素，依此类推，直到队列变空。
三、BFS的代码实现
1.问题一代码如下
| (1).返回的遍历序列是向量的情形，此代码基于图的邻接矩阵 |
#include
#include
#include
using namespace std;
template//表示边的变量可以为整数，也可以为字符串，所以在这里使用模板T
class Graph {
public:
vector> NeighMatrix;//邻接矩阵
vector EdgeList; //表示点集的向量，可以是整型或字符型,所以这里用模板表示
Graph(vector> Matrix, vector edgelist) //利用邻接矩阵和边集对图实例化
{
NeighMatrix = Matrix;
EdgeList = edgelist;
}
int FirstNeighbour(int node) //定义一个成员函数，用来获取某个节点的首个相邻节点
{
for (int j = 0; j < NeighMatrix.size(); j++)
if (NeighMatrix[node][j] != 0)
return j;
return -1;
}
int NextNeighbour(int node, int subnode) //定义一个成员函数，用来获取某个节点在节点subnode后的下一个邻接点
{
for (int j = subnode + 1; j < NeighMatrix.size(); j++)
if (NeighMatrix[node][j] != 0)
return j;
return -1;
}
vector BFS(int start) //人为规定起点，返回BFS遍历节点的索引[0~num-1]
{
queue que;//定义一个队列，用于BFS
vector note;//若需要遍历结果作为向量形式的返回值，用note存储遍历结果
vector visitmark(NeighMatrix.size(), 0);//访问标记向量，某元素索引i未被访问过时，visitmark[i]=0，否则为1
que.push(start);//先把起点推入队列
visitmark[start] = 1;//起点被访问
cout << "startpoint=" << EdgeList[start] << ",result=";
cout << EdgeList[start] << " ";
while (que.size()) //循环体进行的条件是队列存在元素
{
int i = que.front();
//把队头元素（节点i）的全部未访问邻接点放到队列中
if (FirstNeighbour(i) != -1)//前提条件是队头元素至少存在一个邻接点
{
if (visitmark[FirstNeighbour(i)] == 0) //若要把该节点推入队列，需要确保该节点未被访问
{
que.push(FirstNeighbour(i));
visitmark[FirstNeighbour(i)] = 1;//节点推入队列，同时标记为已访问
cout << EdgeList[FirstNeighbour(i)] << " ";
}
int j = FirstNeighbour(i);
if (j == -1)
break;
while (NextNeighbour(i, j) != -1) //节点i的邻接节点中，存在下一个与i相邻的节点
{
if (visitmark[NextNeighbour(i, j)] == 0)
{
que.push(NextNeighbour(i, j));
visitmark[NextNeighbour(i, j)] = 1;
cout << EdgeList[NextNeighbour(i, j)] << " ";
j = NextNeighbour(i, j);//继续迭代，直到节点i的所有相邻节点全部被访问
}
else
j = NextNeighbour(i, j);//若没有这行代码，有可能进入死循环
if (j == -1)
break;
}
}
note.push_back(que.front());
que.pop();//每次循环找出队头元素的所有未访问邻接点，放到队尾，再删去队头元素，这是一个有限的过程
}
cout << endl;
return note;
}
};
int main()
{
vector> Matrix;
vector subMatrix, edge,ans;
int num;
cin >> num;
//输入邻接矩阵
for (int i = 0; i < num; i++) {
edge.push_back(i + 1);//这里用1表示第一个节点
Matrix.push_back(subMatrix);
for (int j = 0; j < num; j++){
int ele;
cin >> ele;
Matrix[i].push_back(ele);
}
}
Graph G = Graph(Matrix, edge);
for (int i = 0; i < Matrix.size(); i++)
ans = G.BFS(i);
return 0;
}
| (2).无返回值的情形,同时设定点集用字符A,B,C,…表示 |
z
#include
#include
#include
using namespace std;
template
class Graph {
public:
vector> NeighMatrix;//邻接矩阵
vector EdgeList; //表示点集的向量，可以是整型或字符型,所以这里用模板表示
Graph(vector> Matrix, vector edgelist) //利用邻接矩阵和边集对图实例化
{
NeighMatrix = Matrix;
EdgeList = edgelist;
}
int FirstNeighbour(int node) //定义一个成员函数，用来获取某个节点的首个相邻节点
{
for (int j = 0; j < NeighMatrix.size(); j++)
if (NeighMatrix[node][j] != 0)
return j;
return -1;
}
int NextNeighbour(int node, int subnode) //定义一个成员函数，用来获取某个节点在节点subnode后的下一个邻接点
{
for (int j = subnode + 1; j < NeighMatrix.size(); j++)
if (NeighMatrix[node][j] != 0)
return j;
return -1;
}
void BFS_void(int start) //人为规定起点，返回BFS遍历节点的索引[0~num-1]
{
queue que;//定义一个队列，用于BFS
vector visitmark(NeighMatrix.size(), 0);//访问标记向量，某元素索引i未被访问过时，visitmark[i]=0，否则为1
que.push(start);//先把起点推入队列
visitmark[start] = 1;//起点被访问
cout << "startpoint=" << EdgeList[start] << ",result=";
cout << EdgeList[start] << " ";
while (que.size()) //循环体进行的条件是队列存在元素
{
int i = que.front();
//把队头元素（节点i）的全部未访问邻接点放到队列中
if (FirstNeighbour(i) != -1)//前提条件是队头元素至少存在一个邻接点
{
if (visitmark[FirstNeighbour(i)] == 0) //若要把该节点推入队列，需要确保该节点未被访问
{
que.push(FirstNeighbour(i));
visitmark[FirstNeighbour(i)] = 1;//节点推入队列，同时标记为已访问
cout << EdgeList[FirstNeighbour(i)] << " ";
}
int j = FirstNeighbour(i);
if (j == -1)
break;
while (NextNeighbour(i, j) != -1) //节点i的邻接节点中，存在下一个与i相邻的节点
{
if (visitmark[NextNeighbour(i, j)] == 0)
{
que.push(NextNeighbour(i, j));
visitmark[NextNeighbour(i, j)] = 1;
cout << EdgeList[NextNeighbour(i, j)] << " ";
j = NextNeighbour(i, j);//继续迭代，直到节点i的所有相邻节点全部被访问
}
else
j = NextNeighbour(i, j);//若没有这行代码，有可能进入死循环
if (j == -1)
break;
}
}
que.pop();//每次循环找出队头元素的所有未访问邻接点，放到队尾，再删去队头元素，这是一个有限的过程
}
cout << endl;
}
};
int main()
{
vector> Matrix;
vector subMatrix;
vector edge;
int num;
cin >> num;
//输入邻接矩阵
for (int i = 0; i < num; i++) {
edge.push_back((char)(65 + i));
Matrix.push_back(subMatrix);
for (int j = 0; j < num; j++) {
int ele;
cin >> ele;
Matrix[i].push_back(ele);
}
}
Graph G = Graph(Matrix, edge);
for (int i = 0; i < Matrix.size(); i++)
G.BFS_void(i);
return 0;
}
| 问题一的输入 |
9
0 1 1 1 0 0 0 0 0
1 0 0 0 1 1 0 0 0
1 0 0 1 0 0 0 1 0
1 0 1 0 0 0 0 1 1
0 1 0 0 0 0 1 0 0
0 1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 1 1 0 0 0 0 0
0 0 0 1 0 0 0 0 0
| 问题一(1)的运行结果 |
startpoint=1,result=1 2 3 4 5 6 8 9 7
startpoint=2,result=2 1 5 6 3 4 7 8 9
startpoint=3,result=3 1 4 8 2 9 5 6 7
startpoint=4,result=4 1 3 8 9 2 5 6 7
startpoint=5,result=5 2 7 1 6 3 4 8 9
startpoint=6,result=6 2 1 5 3 4 7 8 9
startpoint=7,result=7 5 2 1 6 3 4 8 9
startpoint=8,result=8 3 4 1 9 2 5 6 7
startpoint=9,result=9 4 1 3 8 2 5 6 7| 问题一(2)的运行结果 |
0
startpoint=A,result=A B C D E F H I G
startpoint=B,result=B A E F C D G H I
startpoint=C,result=C A D H B I E F G
startpoint=D,result=D A C H I B E F G
startpoint=E,result=E B G A F C D H I
startpoint=F,result=F B A E C D G H I
startpoint=G,result=G E B A F C D H I
startpoint=H,result=H C D A I B E F G
startpoint=I,result=I D A C H B E F G
2.问题二的分析
这个题和上一题的相同之处在于，可以使用BFS的思想，找出图中的一个陆地点，以这个点为中心进行广度优先搜索，此时，若某个节点被访问，直接把这个节点所在位置的元素由1变为0，直到搜索不到陆地，则此时陆地数量+1，为了后续岛屿的寻找，把这个陆地上的所有点变为0，同时继续向右或者向下找陆地点，重复这个过程
代码如下：
| 岛屿数量问题的BFS代码，leetcode击败了65%的C++用户，若想在leetcode运行需要去掉main函数· |
#include
#include
#include
using namespace std;
class Solution {
public:
class Node {
public:
int x;
int y;
Node(int xx, int yy) {
x = xx; y = yy;
}
};
int numIslands(vector>& grid) {
vector> dir = { {1,0},{-1,0},{0,1},{0,-1} };//定义4个方向
queue que;//BFS所用的队列
int cnt = 0;//计数器
int ii = 0, jj = 0;
int xlen = grid.size();
int ylen = grid[0].size();
while (ii < xlen && jj < ylen)
{
if (grid[ii][jj] == '1') //第ii行jj列的点是陆地
{
grid[ii][jj] = '0';
Node start=Node(ii,jj);
que.push(start);
int i = ii, j = jj;
while (que.size())
{
i = que.front().x;
j = que.front().y;
for (int m = 0; m < 4; m++) //把队头点的相邻陆地节点全部找出
{
int xx = i + dir[m][0];
int yy = j + dir[m][1];
if (xx < 0 || xx >= xlen || yy < 0 || yy >= ylen)
continue;//若移动点越界，立刻跳过本次循环
if (grid[xx][yy] == '1')//说明此处还是陆地
{
Node point = Node(xx, yy);
que.push(point);
grid[xx][yy] = '0';//为防止重复访问，此处变为0
}
}
que.pop();//grid[ii][jj]四周的点全部被推入队列，此时这个点弹出队
}
cnt += 1;
}
if (jj < ylen - 1)
jj += 1;
else{ii += 1; jj = 0;}
}
return cnt;
}
};
int main()
{
vector> island{ {'1','1','0','0','0' }, { '1','1','0','0','0' }, { '0','0','1','0','0' }, { '0','0','0','1','1' } };
Solution a;
cout << a.numIslands(island);
return 0;
}