五点差分法求解偏微分方程（PDE）
先以一个例题带大家了解五点差分法求解PDE
偏微分方程的解析解通常是非常难求的，即使是多数常微分方程，通常也难以计算解析解，即使可以计算，那也是相当复杂，因此，微分方程数值解的求解，是我们的一个重要的研究方向
求解微分方程数值解的核心，就是用差商来代替微商，
可以取一个比较小的值
二阶向前差商
二阶向后差商
二阶中心差商
差商有多种形式，我们选择中心差商
同理，y对x的二阶中心差商
由题目条件
可以确定边界取值，这是Dirchilet边界条件
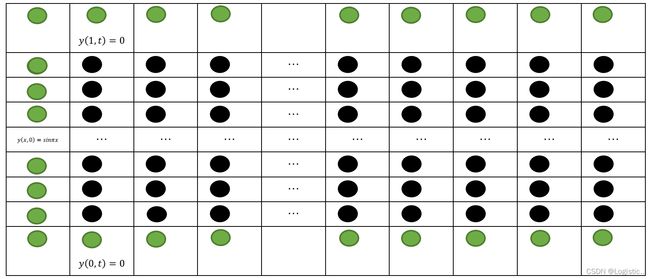
下图是Dirchilet边界条件的直观解释，绿色点代表已知点。
由题目条件
可以确定
附近点的取值，这是Neumann边界条件
用差分可以近似表示成
下图是Neumann边界条件的直观解释，灰色点代表其他已知点，绿色点代表Neumann边界条件确定的点。
由题目条件
可以得出
的近似关系
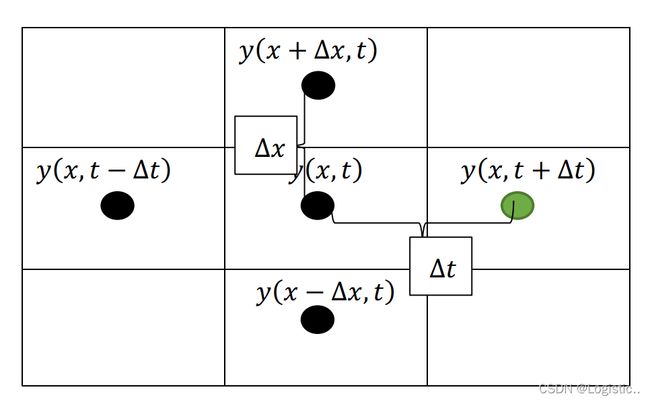
利用网格可视化
我们发现，
可以由左边的4个点近似计算,这就是五点差分法求解偏微分方程的思路,我们把视角放大到整体.
Step1：先看绿色的点1，根据1左侧个点的取值，由(*),可以推出点1的取值
Step2：再看绿色的点2，根据2左侧个点的取值，由(*),可以推出点2的取值，以此类推，可以得出每一列上下两点之外每个点的取值，第三列点的取值，用前两列的点就可以确定
由边界条件
，我们可以发现，x=0和x=1的取值是确定的，
Step3: 重复这个过程，在
空间内的所有离散的近似解已经确定了
下面是本题的Matlab代码
注意，要单独编写一个M文件定义函数
flucfun.m
%y_tt=y_xx,00
%y(x,0)=sin(pi*x),y_t(x,0)=x(1-x),0<=x<=1
%y(0,t)=y(1,t)=0,t>0
%上面是某个波动方程
%这里定义了x范围在0~1，所以x的取值范围是确定的，我们需要t的取值范围
%这里利用五点差分法求解二阶偏微分方程，所以我们需要选择每个自变量的差分步长，分别用dx，dt表示
%yy是波动方程在给定的某个区域内各点的取值，trange是t的取值范围，dx，dt分别代表x，t分量差分的精度
function yy=flucfun(trange,dx,dt)
xrange=1;%为了形式规范，还是写了xrange，xrange可有可无
numX=ceil(xrange/dx);%ceil是向上取整函数，由于matlab以矩阵的形式存储解集，矩阵的大小表示了在这个解集内的离散点数量
numT=ceil(trange/dt);
yy=zeros(numX,numT);
yy(1,:)=0;yy(numX,:)=0; %Dirchilet边界条件
for xx=1:numX
yy(xx,1)=sin(pi*xx*xrange/numX);%Dirchilet边界条件
yy(xx,2)=yy(xx,1)+dt*(xx*xrange/numX)*(1-xx*xrange/numX);%Neumann边界条件
end
for tt=2:numT-1
for xx=2:numX-1
%中间差分
yy(xx,tt+1)=((dt/dx)^2)*(yy(xx+1,tt)-2*yy(xx,tt)+yy(xx-1,tt))+2*yy(xx,tt)-yy(xx,tt-1);
end
end
end
Matlab主程序
xrange=1;
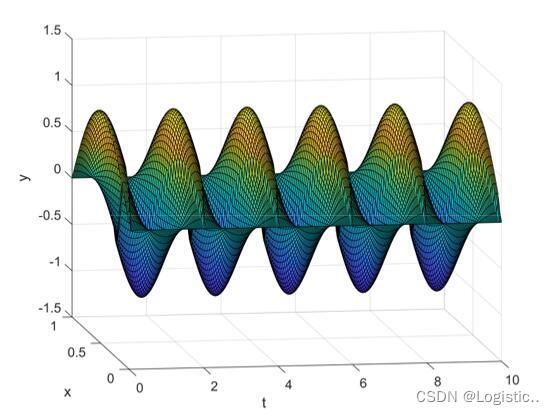
trange=10;%我们想要0这是Matlab的求解结果
编写一个求解给定任一点的函数值的m文件
getvalue.m
function yf=getvalue(xx,tt,yy,x,t)
%求解任给一个(x,t)对应的y值
%xx，tt表示坐标，是两个单调增加的向量
%yy表示求解出来的矩阵
[~,m]=size(xx);
[~,n]=size(tt);
for i=1:m-1
if (xx(i)<=x)&&(x<=xx(i+1))
break
end
end
for j=1:n-1
if (tt(j)<=t)&&(t<=tt(j+1))
break
end
end
yf=yy(i,j);
前提是差分精度足够高！
感谢大家的观看！制作不易