优美的曲线(含蝴蝶线)-CoCube
复现如下这篇:
优美的曲线-turtlesim
两段视频:
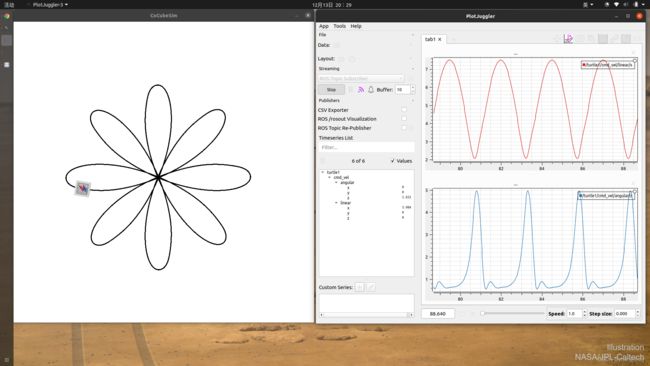
优美的曲线-CoCube
butterfly蝴蝶曲线之CoCube篇
如何更深入分析,获得更高精度曲线呢?
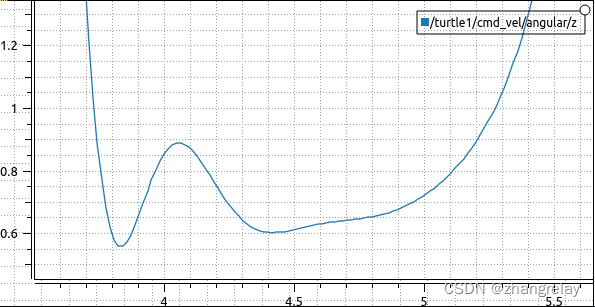
对比下面两幅图:
尤其需要注意右图,右下角。
什么原因导致这个控制量波动?
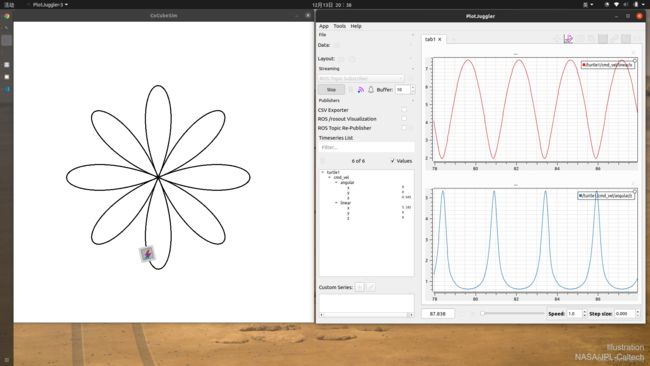
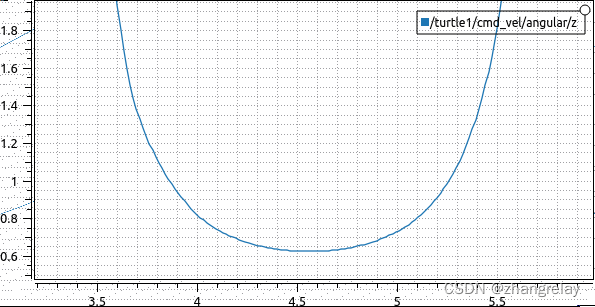
调整控制器参数后。
同样注意右下角:
参数调整对于控制器性能的影响也是非常显著的。
这也就是在机器人系统中为何要充分掌握好,反馈控制器设计的各种理论和方法。
蝴蝶线:
goal_x=9.5+2.0*sin(curve_t/200.0)*(exp(cos(curve_t/200.0))-2.0*cos(curve_t/50.0)-pow(sin(curve_t/2400.0),5));
goal_y=9.5+2.0*cos(curve_t/200.0)*(exp(cos(curve_t/200.0))-2.0*cos(curve_t/50.0)-pow(sin(curve_t/2400.0),5));一个有bug需修改的移动到目标点的示例代码:
#include "ros/ros.h"
#include "turtlesim/Pose.h"
#include "geometry_msgs/Twist.h"
#include "math.h"
#include
ros::Subscriber sub;
ros::Publisher pub;
float goal_x = 2;
float goal_y = 2;
void sendVel(const turtlesim::Pose::ConstPtr& data){
ros::NodeHandle n;
pub = n.advertise("/turtle1/cmd_vel",100);
float curr_x = data->x;
float curr_y = data->y;
float curr_ang = data->theta;
float dist = sqrt(pow(goal_x-curr_x,2) + pow(goal_y-curr_y,2));
std::cout << "Distance = " << dist << std::endl;
if(dist > 0.01){
double ang = atan2((float)(goal_y-curr_y),(float)(goal_x-curr_x));
std::cout << "Curr_ang = " << curr_ang << " | ang = " << ang << std::endl;
geometry_msgs::Twist t_msg;
t_msg.linear.x = 1.0*(dist);
t_msg.angular.z = 4.0*(ang-curr_ang);
pub.publish(t_msg);
}
else
{
std::cout << "Mission Completed" << std::endl;
std::cout << "Please enter new coordinates" << std::endl;
std::cout << "Please enter goal_x:" << std::endl;
std::cin >> goal_x;
std::cout << "Please enter goal_y:" << std::endl;
std::cin >> goal_y;
}
}
int main(int argc, char **argv){
ros::init(argc,argv,"goToGoal");
ros::NodeHandle n;
sub = n.subscribe("/turtle1/pose",100,sendVel);
ros::spin();
return 0;
} 机器人CoCube沿着这些点走起来,轨迹就是一条连续的曲线。
它的足迹就是依据数学公式描述之优美的曲线。
如下这篇是点:
从开环到闭环的旅程-CoCube
好算法好参数,对于机器人轨迹跟踪而言非常重要。
这些和实际系统有何关联呢?
迷宫逃离的问题-CoCube
将轨迹跟踪算法用于上图红色轨迹线,就可以实现机器人穿越迷宫哦。
相关算法不断完善,就可以用于下图:
这类地图+动态环境识别,如果都能处理好,一个简易的自动导航机器人就完工啦。
下一讲,不用下面这样的环境了:
目标实现不可能一帆风顺,在自由的环境中随心所欲的留下自己的足迹。
一定会遇到各种艰难险阻,有可预知的,静态障碍物,或不可预知的,动态障碍物,或者两者皆有。
怎么办?
^_^
参考引用:
复杂环境移动机器人路径规划与轨迹跟踪研究
罗敏
【摘要】:随着世界各国经济和科学技术的飞跃发展,移动机器人的应用领域越来越广泛,其应用场景也从室内环境拓展到了各种复杂环境,如野外、水下、空中甚至外太空等。目前,对于复杂环境的机器人系统仍存在许多尚待研究的课题。本文针对环境全局信息已知、地面崎岖不平的复杂环境条件下的轮式机器人的路径规划和轨迹跟踪控制技术进行研究。本文建立了崎岖地面的环境模型,针对曲面路径规划算法的时间复杂度改进问题,提出了多尺度技术。针对曲面路径规划算法的精度改进问题,提出了曲面的二维等效展开技术。在已规划的崎岖地面最优路径的基础上进行了曲面轨迹跟踪控制研究,在基于力矩受限的约束条件下,提出了基于梯度下降参数优化法的调节时间指标和最大力矩导数的优化改进方法。并对复杂环境下崎岖地面的不平性和机器人拐弯等产生的不确定性干扰影响进行了轨迹跟踪控制算法研究和分析。主要工作如下:首先,针对曲面轮式机器人的路径规划,提出了减小路径规划算法时间复杂度的多尺度图法。常用路径规划算法的时间复杂度会随着规划场景的节点规模增大呈指数性增长。对于复杂大规模场景的崎岖地面规划,运用这类路径规划算法时的时间成本代价太大。本文提出的多尺度法,通过在粗-细尺度图上求取最优路径,减小了节点数增多对时间复杂度增长的影响,从而减小了路径规划算法的时间成本。崎岖地面的节点规模越大,多尺度法在时间复杂度上的改善效果越好。本文还将多尺度法拓展应用到了多机器人的路径规划上。其次,针对曲面轮式机器人的路径规划,提出了减小路径规划算法的路径长度误差的二维等效展开方法。由于传统路径规划算法通常基于节点间的欧几里得距离公式计算最优路径,将传统算法应用于曲面最优路径规划时,曲面上节点之间的距离和节点间的空间欧几里得距离之间存在误差。二维等效展开方法通过计算二维等效曲面上的路径长度,减小了路径规划算法的最优路径长度误差。崎岖地面的凹凸不平度越大或崎岖地面的节点规模越大,二维等效展开方法在计算曲面最优路径长度时的误差改善效果越好。本文将二维等效展开方法也拓展应用到了多机器人的路径规划上。然后,针对曲面轮式机器人的轨迹跟踪,提出了具有力矩约束的调节时间优化方法。由于通常的轨迹跟踪控制算法设计得到的输入力矩常常超过实际应用中的最大饱和值,使得轨迹跟踪算法的实用性变差,所以在算法设计时应该控制输入力矩的峰值大小。减小力矩通常会牺牲系统调节时间指标,设计时不应因控制力矩使得调节时间过大而使算法无法实际应用。本文提出的具有力矩约束的调节时间优化法将输入力矩最大值控制在期望值上,同时得到尽可能小的调节时间,保证了算法的实用性。该优化方法通过将输入力矩最大值减小到理想的期望值上,节约了移动机器人运行时所需要的能源。输入力矩峰值的减小,也降低了机器人电机运行所需的功率,因而减小了电机等机械设备的物理尺寸。最后,针对曲面轮式机器人轨迹的跟踪,提出了具有力矩约束的力矩导数最大值优化方法。通常的轨迹跟踪算法设计得到的输入力矩在施加力的初始时刻会出现时间很短的突然变化很大的冲击负荷,这种冲击负荷对移动机器人的电力设备和机械结构都会产生危害,影响设备的使用寿命。力矩导数最大值优化方法在限制力矩最大值和系统调节时间的基础上,尽量地减小系统的最大力矩变化率,让机器人启动的起步过程平滑,降低了启动过程中的冲击负荷,减小了对机器人的电力设备和机械设备的负荷要求和机械尺寸要求。对输入力矩导数的最大值的优化,使得需要的力矩输入很小,可以有效地节约能源。