多标签分类器（附pytorch代码）

多标签分类器

 多标签分类任务与多分类任务有所不同，多分类任务是将一个实例分到某个类别中，多标签分类任务是将某个实例分到多个类别中。多标签分类任务有有两大特点：

• 类标数量不确定，有些样本可能只有一个类标，有些样本的类标可能高达几十甚至上百个
• 类标之间相互依赖，例如包含蓝天类标的样本很大概率上包含白云

如下图所示，即为一个多标签分类学习的一个例子，一张图片里有多个类别，房子，树，云等，深度学习模型需要将其一一分类识别出来。

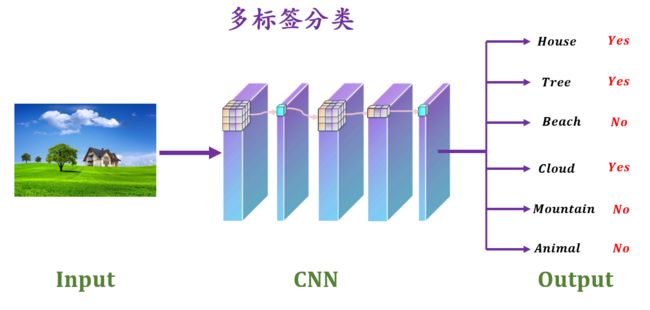
多标签分类器损失函数

 假设$\mathcal{X}={\mathbb{R}}^d$表示$d$维样本空间，$\mathcal{Y}=\{y=(y_1,y_2,\cdots ,y_n)|y_i\in \{0,1\},i=1,\cdots ,n\}$表示$n$维标签空间。训练该多标签分类器的损失函数可以用二元交叉熵函数，该多标签分类器的最后一层为$\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}$，多标签分类模型预测的概率向量为$p=(p_1,p_2,\cdots ,p_n)$，其中$p_i\in [0,1](i=1,\cdots ,n)$，此时真实标签分布$y$和预测概率分布$p$的二元损失函数为：$$\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}1=-\frac{1}{n}\sum _{i=1}^n[y_i\log p_i+(1-y_i)\log (1-p_i)]$$

代码实现

  针对图像的多标签分类器pytorch的简化代码实现如下所示。因为图像的多标签分类器的数据集比较难获取，所以可以通过对mnist数据集中的每个图片打上特定的多标签，例如类别$1$的多标签可以为$[1,1,0,1,0,1,0,0,1]$，然后再利用重新打标后的数据集训练出一个mnist的多标签分类器。

from torchvision import datasets, transforms
from torch.utils.data import DataLoader, Dataset
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import os

class CNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.Sq1 = nn.Sequential(         
            nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=2),   # (16, 28, 28)                           #  output: (16, 28, 28)
            nn.ReLU(),                    
            nn.MaxPool2d(kernel_size=2),    # (16, 14, 14)
        )
        self.Sq2 = nn.Sequential(
            nn.Conv2d(in_channels=16, out_channels=32, kernel_size=5, stride=1, padding=2),  # (32, 14, 14)
            nn.ReLU(),                      
            nn.MaxPool2d(2),                # (32, 7, 7)
        )
        self.out = nn.Linear(32 * 7 * 7, 100)  

    def forward(self, x):
        x = self.Sq1(x)
        x = self.Sq2(x)
        x = x.view(x.size(0), -1)    
        x = self.out(x)
        ## Sigmoid activation   
        output = F.sigmoid(x)  # 1/(1+e**(-x))
        return output

def loss_fn(pred, target):
    return -(target * torch.log(pred) + (1 - target) * torch.log(1 - pred)).sum()


def multilabel_generate(label):
    Y1 = F.one_hot(label, num_classes = 100)
    Y2 = F.one_hot(label+10, num_classes = 100)
    Y3 = F.one_hot(label+50, num_classes = 100) 	
    multilabel = Y1+Y2+Y3
    return multilabel
        
# def multilabel_generate(label):
# 	multilabel_dict = {}
# 	multi_list = []
# 	for i in range(label.shape[0]):
# 		multi_list.append(multilabel_dict[label[i].item()])
# 	multilabel_tensor = torch.tensor(multi_list)
#     return multilabel

def train():
    epoches = 10
    mnist_net = CNN()
    mnist_net.train()
    opitimizer = optim.SGD(mnist_net.parameters(), lr=0.002)
    mnist_train = datasets.MNIST("mnist-data", train=True, download=True, transform=transforms.ToTensor())
    train_loader = torch.utils.data.DataLoader(mnist_train, batch_size= 128, shuffle=True)


    for epoch in range(epoches):
    	loss = 0 
    	for batch_X, batch_Y in train_loader:
    		opitimizer.zero_grad()
    		outputs = mnist_net(batch_X)
    		loss = loss_fn(outputs, multilabel_generate(batch_Y)) / batch_X.shape[0]
    		loss.backward()
    		opitimizer.step()
    		print(loss)

if __name__ == '__main__':
	train()