为了统计一切出现在图像上的目标类别的计数：Learning To Count Everything 论文笔记

写在前面
  这是一篇关于目标计数的文章，5月份CVPR出来的时候看过了，这里总结一下，为下一篇做铺垫。代码我试过了，比较管用。强推！

• 论文地址：Learning To Count Everything
• 代码地址：GitHub
• 第一次更新：2022年5月3日，多看了一些文章，本文归属于 类别无关的单类别计数问题，即一张图片中只有一个类别，但是总的图库里面类别很多。

一、Abstract

  目前的工作主要关注于单类别特定目标的计数，而本文关注一种很牛皮的概念，Counting Everything：在某个类别给出少量标注的情况下来统计该类别，这也就是作者提出的一种few-shot少样本回归任务。为了解决该任务，本文利用给出的图像和少量样本来预测图像中所有样本的密度图。同时作者提出了一种新的自适应策略在测试时来调整网络以泛化到任何新的类别上，而这只需要少量该新类别的样本。同时作者引入了新的数据集(FSC-147)，包含147个目标类别6K张图像，标注为Boxes标注和点标注，确实牛皮。

二、引言

  现有的计数任务存在两大主要挑战：1、将计数任务作为有监督的回归任务，需要大数量的点标注，费时且费力；2、没有一种通用的数据集（包含多类别）。
  本文解决了上述的两个挑战，针对问题1：将计数任务作为典型的全监督方式，提出一种少样本回归任务。该任务采用一幅图片以及少量的示例样本作为输入，输出则为标记的样本数量。与一般的计数任务不同，本文设置的训练集和测试集的类别分布不同（增加了难度）。
  本文提出了新的架构Few Shot Adaptation and Matching Network (FamNet)来解决少样本计数问题，主要由两个模块组成：1、特征提取模块，用于解决目标类别数量的问题；2、稠密预测模块，用于解决类别无关的挑战。另外，作者表明在测试阶段采用一种新颖的少样本适应方法来提高FamNet的性能。
  为了解决少样本计数数据集缺乏的问题，作者引入了一个中等规模的数据集FSC-147包含超过6K张图片147个类别。数据标注采用点标注和回归框标注。
  本文贡献如下：1、提出将目标计数作为少样本回归任务；2、FamNet+ adaptation scheme；3、少样本计数数据集: FSC-147。

三、Related Works

  之前的计数方法一般用于特定类别的计数，所需训练样本也是成千上万。还有一些少样本计数的工作既需要点的标注也需要Bounding boxes，或者会受到遮挡的影响。然后是一些密度检测的方法，一般多用于人群或者细胞计数。与本文相似的工作还有HAML，但是该方法在训练时引入了二阶导数，使得计算偏昂贵，而本文提出的方法既快速又准确。

四、少样本适应与匹配网络

4.1 网络结构

输入为一张带有少数Bounding boxes+其他目标点的图像，输出为一张密度图以及目标的数量。FamNet主要由两个关键模块组成：1、多尺度特征提取模块，ResNet-50→layer3+layer4，利用ROI Pooling（阅读源码，确实是个简单的Pooling，而且还不是用C++编译好的版本，直接用的Pytorch搭建的Pooling，这地方要是换成ROIAlign估计性能得提高一两个点）获得多尺度特征；2、密度预测模块，采用样本特征和图像特征之间的关联图（直接用样本特征和图像特征进行卷积）作为密度预测模块的输入。同时为了统计多尺度的目标，将样本特征尺度缩放发到不同的尺度（0.9，1.1倍）下，然后用图像特征来关联样本特征（卷积）从而获得多个关联图，最后将关联图拼接并送入到密度预测模块中。密度预测模块由5个卷积和3个下采样层（下采样2倍）组成。

4.2 训练

  采用自己构建的数据集进行训练。构建密度图的过程：使用适当的窗口尺寸进行高斯平滑。具体来说，首先采用点标注来估计目标的尺寸：计算每一个点和最近邻点的距离以及所有点的平均距离，这一平均距离作为高斯滑动窗口的尺寸用来产生密度图，高斯分布的标准差设为窗口尺寸的四分之一。
  损失采用mean squared error均方误差(MSE)，Adam优化器，$lr=10^{-5}$，batch_size=1，image_h = 384，image_w根据原始长宽比进行调整。

4.3 测试阶段适应

  在推理阶段，提出一种新方法用于提升估计模块的精度，关键在于充分利用Bounding boxes样本的位置信息（在训练阶段利用的是样本外观特征信息）。主要是两种损失函数：

4.3.1 最小计数损失

  对于每一个给定的样本框$b\in B$，$B$为给定的所有样本框，$Z_b$表示在密度图$Z$上位置$b$处的裁剪图，均有${\Vert Z_b\Vert }_1\ge 1$，而${\Vert Z_b\Vert }_1$为$Z_b$所有值的求和。定义最小计数损失如下：
$${\mathcal{L}}_{\text{MinCount }}=\sum _{b\in B}\max \left(0,1-{\Vert Z_b\Vert }_1\right)$$
（查看源码可知，此处当${\Vert Z_b\Vert }_1\ge 1$时，${\mathcal{L}}_{\text{MinCount }}=0$。因此，最小计数损失只会惩罚那些没有判断出样本点区域内目标大于1的情况）

4.3.2 扰动损失

  这一损失受到目标跟踪里的相关滤波算法所激发。给定待追踪的目标，这些算法会学得一个滤波器能够对精确位置处的bounding boxes进行高强度反应，而对干扰位置处的响应较低。然后这些相关滤波器就可以根据干扰位置到目标位置处的值进行回归优化，其中目标回应值会随着干扰距离的增加而呈指数衰减，通常为高斯分布。
  本文得出的密度图$Z$本质上为样本和图像的关联响应（卷积）图。而样本点周围的密度值理想情况下也会是一个高斯分布。设$G_{h\times w}$为尺寸是$h\times w$的2D高斯分布图，干扰损失定义如下：
$${\mathcal{L}}_{Per}=\sum _{b\in B}{\Vert Z_b-G_{h\times w}\Vert }_2^2$$
（此损失一定存在！）

4.3.3 联合适应损失

$${\mathcal{L}}_{\text{Adapt }}={\lambda }_1{\mathcal{L}}_{\text{MinCount }}+{\lambda }_2{\mathcal{L}}_{\text{Per }}$$
其中${\lambda }_1,{\lambda }_2$为超参数。
  测试时采用100个梯度下降步长，$lr=10^{-1}$，${\lambda }_1=10^{-9},{\lambda }_2=10^{-4}$。为什么要设这么小？原因是确保适应损失和训练损失在同一量级上。注意：适应损失仅仅用在测试阶段（这估计得看代码才能知道如何操作的：训练和测试分开，测试时继续迭代损失更新网络，步长为100）。

五、FSC-147数据集

  现有的计数数据集大多服务于某种特定的类别，例如车、人、细胞。另外，现有的多类别数据集并未包含很多的图像。还有一些数据集，图像的目标实例数量太少或者外观尺寸变化不够显著等因素使得这类数据集也不适用。因此，本文收集了6135张，共147个类别的图像，主要由厨房餐具、办公文具、信纸、交通工具、动物等组成。数量从7-3731，平均每幅图56个目标。每个目标实例用近似中心(?)的点来标注。另外，三个目标实例随机挑选出来加上矩形框作为目标样例。接下来就是制作数据集的过程，这里略去，感兴趣的童鞋可以查看原论文。注意一下数据集的划分：训练集：3659张，89类；验证集：1286张，29类；测试集：1190张，29类，总计147类。

六、实验

6.1 性能评估指标

• 均方绝对误差：$MAE=\frac{1}{n}{\sum }_{i=1}^n\left|c_i-{\hat{c}}_i\right|$
• 均方根误差：$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(c_i-{\hat{c}}_i\right)}^2}$，其中$n$为测试图片的数量，$c_i,{\hat{c}}_i$为GT和预测的数量。

6.2 与其他少样本方法的比较

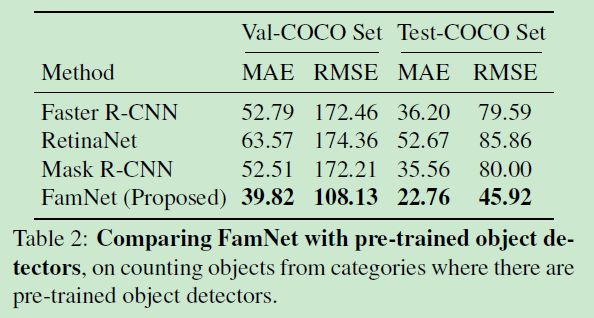
6.3 相比于目标检测的方法

6.4 消融实验

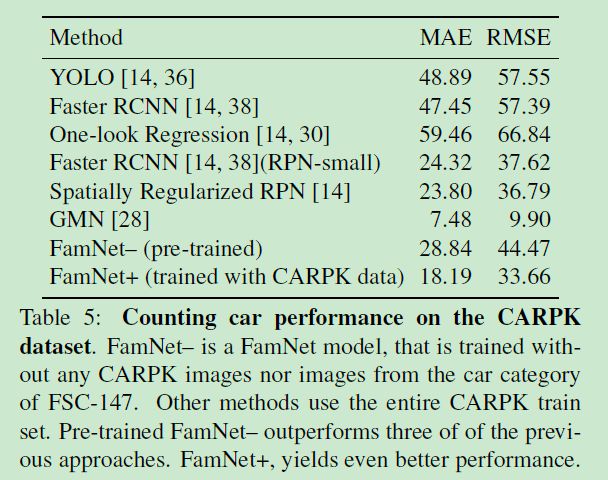
6.5 特定类别的目标计数

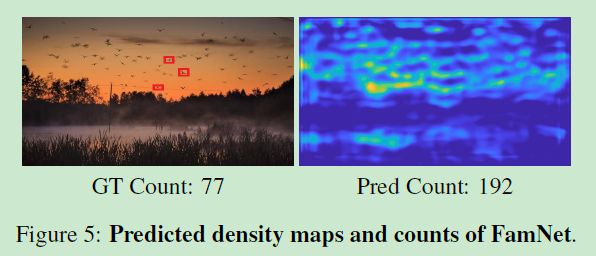
6.6 高质量的结果

七、结论

  本文提出一种少样本计数回归任务与相应的计数数据集，并设计了一种新的方法用于该任务，性能很好。
写在后面
  本文主要是起一个引导作用，开创了少样本计数任务以及相应的数据集，提供了Baseline以供研究人员进行改进，方法部分讲的不是太详细，建议阅读源码~

更新
2021年12月28日第一次更新：结合源码对构建网络的关键模块进行了补充，详见括号内内容~