统计学分析方法

多变量分析方法的选择

1、有因变量，则建立有监督模型。

有监督模型有两大通用目的：1）分析哪些自变量对因变量存在显著影响作用；

                           2）通过选择对因变量存在显著影响的自变量，建立预测因变量取值的预测模型

1）因变量为连续变量，建立的模型称为回归预测模型：
            自变量为连续变量时，可选择回归分析、方差分析；
            自变量为分类变量+连续变量，可选择带虚拟变量的回归分析、联合分析、方差分析
2） 因变量为分类变量（定性数据），建立的模型称为分类预测模型：
            自变量为连续变量（或连续+分类）时，可选择判别分析、Logistic/probit analysis
            自变量为定性数据时，可选择对数线性回归（Logit）。预测因变量是如何分类的，在人文社科常用。

2、无因变量，则建立无监督模型。

只要是无监督分析，都叫做描述分析，分析方法得到的结果没有客观标准判断结论是否准确。

目的：1）对人进行分类；2）对变量/指标进行分类；3）分析变量与变量之间的测量关系

1） 自变量为连续变量时，选择因子分析（其中一个目的就是对变量/指标分类）、聚类分析（对人分类、对变量/指标分类）
2）自变量为分类变量时，选择对应分析（对人分类）、多维尺度分析（对人分类）

3、其他分析

1） 当模型中需要加入潜在变量（通过多个客观指标测量的抽象概念整体）、或需要考虑多个变量之间的因果关系分析模型，建立结构方程模型、路径模型、协方差分析。

2）综合评价：通过多个指标对多个评价对象进行排名，可选择层次分析法（AHP)、因子分析等。

相关系数

1、相关系数是衡量两个变量之间变化趋势的相关性

2、不同变量类型的相关系数

    两个变量都为连续变量，则可用Pearson相关系数。在统计中常用r这个符号来表示。
    两个变量都为定序变量，则可用GMMA、Spearman、Kendall’s tau-b等相关系数
    两个变量都为定类变量，则可用LAMMDA等相关系数
    一个变量为定类变量，一个变量为连续变量，可通过ETA系数来测量相关性

3、三种重要相关系数

    Pearson相关系数：参数检验，针对两个都是连续变量的数据进行相关性判断
    Spearman相关系数：非参数检验，针对两个都是定序变量
    Kendall’s tau-b相关系数：非参数检验，针对两个都是定序变量

4、其他概念

常用方法：散点图；计算相关系数

4、相关分析的假设检验

原假设：两个变量来自总体中不存在显著相关性

研究假设：两个变量来自总体中存在显著相关性

显著性检验目的：是用来判断两个变量在总体中是否存在相关性(<0.05，研究假设成立)

相关系数目的：是计算两个变量在样本数据中的相关性强弱

操作：分析-相关-双变量

5、偏相关分析的假设检验

注意：计算相关性的变量为连续变量，加入控制的变量同样也是连续变量

操作：分析-相关-偏相关性

回归分析

1、目的与应用

    目的：当需要用一个数学表达式（模型）表示多个因素与另外一个因素之间关系时，可选用回归分析法。

     R2：自变量对因变量的解释能力，即r（相关系数）的平方。注意r不一定是一元一次回归模型里x前面的值，x前面的值是要考虑x和y的量纲的。

应用：和有监督模型的两个通用目的相同：

1）分析哪些自变量对因变量存在显著影响作用，R2值可以不要求大于0.8；

2）通过选择对因变量存在显著影响的自变量，建立预测因变量取值的预测模型，模型R2必须要求大于等于0.8。

但是，在人文社科领域，很多回归模型的R2值达不到0.8，也可以用来做预测。

2、回归分析的建立步骤

1）选择变量

        因变量：根据研究需求或问题推导出来

        自变量：1）前人的研究成果；2）个人经验

2）确定自变量与因变量之间关系

        首先，挨个将自变量与因变量画散点图，判断每个自变量与因变量间是线性还是非线性关系

        其次，通过卡方检验、T检验、F检验或相关分析法，挨个分析每个备选的自变量与因变量之间是否存在显著的相关性。将与因变量明显没有相关性的自变量剔除掉，不加入到后期模型中

3）选择对应的线性或非线性方程，进行各项参数计算

4）回归方程计算，对模型进行全方位检验

多重共线性检验：检验多个自变量之间是否存在相关性较高的变量，如有，则保留与因变量相关性最高的一个自变量。（相关分析法、VIF/容忍度）

模型拟合优度检验：方差检验/判定系数（R方）/残差检验/自变量参数检验

3、回归分析的软件操作

画图位置：图形-图表构建器

解决问题：分析影响人们家庭收入的因素有哪些，建立预测收入的回归方程

因变量：家庭收入

自变量：年龄、工作年限、性别（因为只有男女01）、学历（变成虚拟变量）

操作：分析-回归-线性（注意：自变量需选择连续变量或者虚拟变量转换的变量）

          “统计”中勾选共线性诊断、DW（残差）

           “图”中勾选标准化残差图下的：直方图、正态概率图

4、虚拟变量

原因：分类变量无法参与到回归模型中的加减乘除运算

操作：将原先的分类编码统一转换为0、1数值

           转换-重现编码为不同变量，定义旧值与新值的转换关系

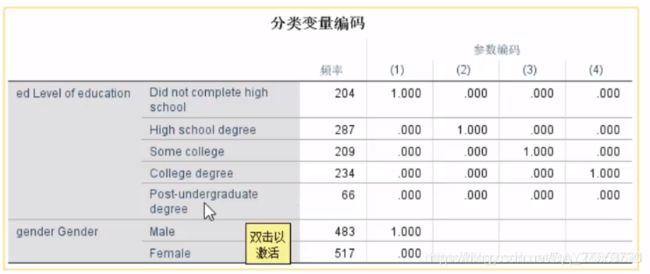
    Ed=12345，转换为4个变量，选择第三个值为对照（也可以选其他值为对照人群）

    还可以转换为5个变量，这时没有对照人群，都有一个1。
  

	1	2	3（对照人群）	4	5
Ed1	1	0	0	0	0
Ed2	0	1	0	0	0
Ed3	0	0	0	1	0
Ed4	0	0	0	0	1

5、回归分析的结果解读

    1）拟合优度检验：

    R方值（R2）

    F值：F值对应的概率P值小于0.05，研究假设成立，即至少有一个自变量对因变量存在显著影响

    2）参数显著性检验：

        根据每个自变量的t值对应的概率P值是否小于0.05，如小于0.05，则研究假设成立，即该自变量对因变量存在显著影响。

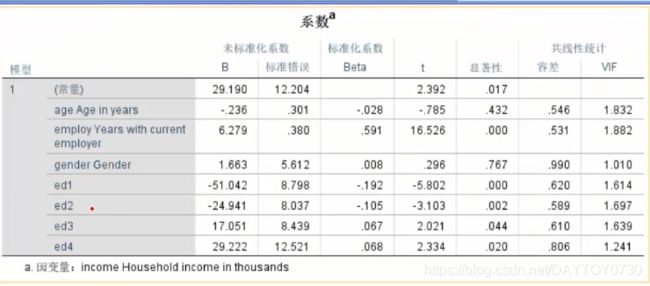
  根据下表得出：

        工作年龄和学历对收入有显著影响，而年龄和性别没有。通过标准化系数来判断两者对影响程度大小，可知工作年限的影响明显大于学历。

        工作年限对收入影响程度（未标准化系数的B）：在其他变量不变的情况下，工作年限每增加一个单位（1年），则因变量家庭收入平均增加6.279个单位。

        学历对收入的影响程度（4个虚拟变量）：Ed1 = -51.042表示Ed1代表的学历（高中以下）比对照的学历人群（大专学历）在因变量家庭收入上，平均低51.042个单位 ——其他同理

3）共线性检验：

        通常根据VIF>10，自变量之间存在共线性。如果存在共线性，可用逐步法解决。

4）残差检验：

        DW越接近2，表示残差越不存在自相关性。——主要看两个图表：直方图、正态P-P图

5）回归方程 

         先通过逐步回归法，将对因变量没有显著影响的自变量从模型中剔除，得到干净的模型

        操作：用逐步回归法，在线性回归的方法中选“步进”，从自变量中将对模型没有影响的因素删除掉。

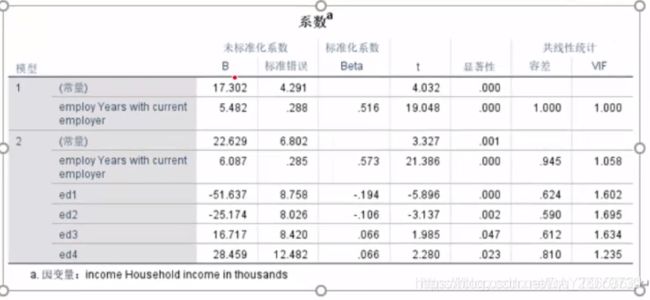
        以下结果为三次逐步回归后，R方值很接近1得到的结果。第三个模型是最准确的

回归方程：y=34.601+6.021*工作年限-62.647*ed1-36.379*ed2

      发现模型中没有ed3和ed4，那就无法完整反应学历的影响。需要强制将他们放到模型里。操作是：任务三-6-32:42，在回归分析中将四个学历放在下一层（SPSS软件里选“下一个”），方法选强制（输入）。得到如下结果

回归方程：y=22.629+6.087*工作年限-51.637*ed1-25.174*ed2+16.717*ed3+28.459*ed4

6）非线性回归

（1）求解方式：

        线性转换：原因是非线性方程拟合方法和参数初始值设置均会导致求出的结果并非全局最优解，因此尽量将非线性方程转换为多元线性回归方程。

        直接建立非线性方程，求解非线性模型。

    操作：先通过散点图判断是否存在非线性关系（用telecon数据）

    SPSS操作1：分析-回归-曲线估算

    ​ 自变量：Ininc；因变量：Income

    ​ Income = e^Ininc

    SPSS操作2：分析-回归-非线性

        因变量：Income
        自己写模型表达式a*EXP(b*Ininc)
        点“参数”设置初始值

因子分析

目的：对多个具有较高相似性的变量/指标进行降维，前提是这些变量/指标之间必须存在一定的相关性/相似性

1、应用场景

    1）降维后做综合评价

    2）效度检验：对抽象概念的测量工具进行有效性检验，判断哪些指标需要保留或删除，并对保留的指标进行维度划分

    3）降维后做其他分析：由于变量存在较高相关性，不适合做回归分析、聚类等其他分析，需要用因子分析消除变量间较高的共线性

2、因子旋转的目的

    1）使得因子可以更好地代表原来的变量

    2）降低或消除提取的因子之间的相关性

3、SPSS软件操作

分析-降维-因子

1）描述-相关性矩阵-KMO和巴特利特球形度检验（用来判断相关性）

2）提取：方法默认选择主成分（输出勾选碎石图 ，也可以不选）

     （主成分分析是因子分析中一种提取因子的方法）

3）旋转-最大方差法  输出-旋转后的解

4）得分-保存为变量

5）选项-按大小排序、排除小系数

4、因子分析的结果解读

   1） KMO>0.7，适合做因子分析

    2）累计方差贡献率需要达到多少才合适：
          做综合评价：>80%（类似于回归分析需要R2>0.8）
          效度检验或其他分析：>60%，效度检验更宽泛，甚至可以不要求

          判断因子数量：因子特征值>1；因子的累计方差贡献率；碎石图拐点位置的因子数量（现在已经比较少用）

   3） 因子的划分：根据每个变量在每个因子中的取值是否大于0.5（最好用旋转后的）

   4）效度检验（应用场景2）（用因子旋转载荷矩阵）：

    用于判断保留哪些变量，这种方法也主要应用于探索性因子分析

        第一判断标准：每个变量有且只有一个因子载荷值大于0.5，如果所有因子载荷值均小于0.5，则说明该变量不具有收敛效度，需要删除；

        第二判断标准：变量在两个或以上因子中的载，荷值同时大于0.5，则说明该变量不具有区分效度，需删除；

        第三判断标准：某变量单独成为一个因子，则说明该变量也不存在收敛效度，需删除

       5）因子原始得分计算（用因子得分系数矩阵）：F1 = x1*a1 + x2*a2……

    因子轴旋转后的因子得分：在变量视图里可以找到几个

Logistic回归（逻辑回归）

1、应用场景：

做分类预测模型，且为非参数检验方法。可以用于二分类、无序多分类、有序多分类（有序多分类前提：自变量对因变量影响是不变的）。

2、SPSS软件操作

二元（因变量有两个值）

1、操作

    位置：分析-回归-二元Logistic

    首先选“输入”方法，统一看下自变量对因变量的影响程度

    分类：将分类变量转为虚拟变量

    保存：概率、组成员

     选项：Exp的置信区间

2、结果解读

    1、很重要的一个结果是“分类表”，用来判断逻辑回归模型的准确率。

    2、看另一个表“方程中的变量”：
        1）根据参数检验中的p是否<0.05，得到自变量对因变量是否存在显著影响。
        2）根据“瓦尔德”（Wald）值的大小，判断自变量对因变量的影响程度

    然后再次进行逻辑回归操作，选“向前”或“向后”方法，剔除影响程度小的变量。

    之后如果发现有的变量被剔除了，可以用分层的方法（选“下一个”），用“输入”方法，强制将某变量加进来

  3、优势比（OR值，在表格中是Exp(B)）大于1，表示该自变量会增加因变量取1的概率的发生；反之会降低因变量取1的概率（B是根据正负号判断）。

   4、连续自变量对因变量的影响程度解读：在其他变量不变的情况下，当年龄增加一个单位（1岁）时，优势比增加1.385倍（年龄越大、退休概率越高）

   

    5、分类自变量对因变量的影响程度解读：

    在Level of education的4个虚拟变量中，只有第3个虚拟变量有显著影响。虚拟变量的对照组是"Post-undergraduate"，第3个虚拟变量是"Some college"。所以这个结果的解读是：在其他变量不变的情况下，大专学历的优势比是研究生学历优势比的0.120倍，即大专学历高于研究生学历的退休概率

    6、Logistic公式：

 

    最后SPSS会自动生成两个变量：

    PRE是指每个人的概率，概率和0.5比较，如果>0.5，则因变量取值。这个0.5是在回归分析中的“选项”里设置“分类分界值”

    PGR是指每个人的因变量取值

多元无序回归

1、操作

        位置：分析-回归-多元Logistic回归

        参考类别选哪个都可以，结果没差别

        因子选分类变量，协变量选连续变量。

        模型中主效应和全因子根据区别情况勾选，详细可看方差分析

        统计里的几个模型可以定制看各个变量的影响

        保存里选择“预测类别”和“预测类别概率”，和二元回归一样。

2、结果解读

似然比检验，根据其显著性的值，可以判断几个自变量和因变量有没有相关性。

参数估算值有两个大表，原因是其实相当于建立了两个二元逻辑回归。

有序多分类回归

1、操作

        分析-回归-有序

        在“输出”勾选“平行线检验”、“预测类别”和“预测类别概率”（平行线检验是检验无论切割在哪里，自变量对因变量的影响是不变的，此前提成立方可建立有序多分类模型）

        位置，选主效应。

2、结果解读

    “模型拟合信息”表：显著性<0.05，说明至少有一个自变量对因变量有影响作用

    “拟合优度”表，显著性>0.05，说明模型的拟合状态还不错。

    “伪R方”，一般不看这个结果。

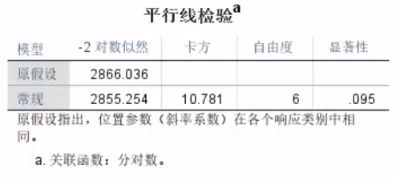
    “平行线检验”，检验当因变量划分不同取值时建立的多个二元Logistic回归，自变量对因变量的影响程度是相同的。如果该检验不成立，则不能选择有序多分类模型，改用无序多分类模型。当P>0.05，说明原假设成立，则平行性检验成立，可以建立有序多分类模型。

     

    “参数估算值”：

        阈值一栏里：对有序变量逐次切割之后做的二元回归

        位置一栏里：“显著性”<0.05的，说明该变量对因变量有显著影响，可将“显著性”>0.05的变量去除后，再重新做一次回归预测

        “参数估算值”：这里没有直接计算出优势比（Exp(B)）,但是“位置”一栏的“估算”就是B。所以可以根据估算值的正负来判断：如果为正，则该参数增加因变量取大于1的概率，如果为负则增加因变量取小于1的概率。

        模型公式：

           第一个：

            p1表示学历取1的概率

           第二个：

            p2表示学历取1和2的概率

          第三个：

             p3表示学历取1、2、3的概率

           第四个：

             p4表示学历取1、2、3、4的概率

时间序列分析

普通ARIMA模型和因果关系ARIMA模型的区别就是，自变量是否要考虑因果关系的滞后性（普通的不考虑）

格兰杰因果检验

因果关系成立的三个条件：       

        1、AB两个事件必须存在相关性

        2、原因A必须发生在结果B之前 

        3、排除其他干扰因素（没有A导致B，或A+C导致B）

平稳序列

ARIMA模型建立的前提是时间序列数据必须为平稳序列，可通过单位根检验（ADF）来判断一个序列是否平稳。如果不平稳，可通过差分进行转换。

ARIMA中的I就是差分进行了几阶差分，如果没有差分就是0

ARIMA模型三个重要参数

p： p阶自回归模型 AR（p）

i： i阶差分

q： q阶移动平均模型 MA(q)

周期性计算

1）通过自相关系数（ACF）的拐点，乘以4得到周期。

2）谱分析，分析—时间序列—谱分析，通过频率取值最高的点对应的频率乘以数据量，得到周期

SPSS软件操作

普通ARIMA模型

    1、定义时间：数据-定义日期和时间

    2、建立模型：分析-时间序列预测-创建传统模型
        加入因变量和自变量（自变量可以不加，在这里添加的自变量是不考虑滞后性的，只有和因变量的相关性）
        方法选“专家建模器”，条件可以自定
        “统计”里的勾选项用于判断模型的好坏
        “图”一般画预测值和拟合值

    结果解读：
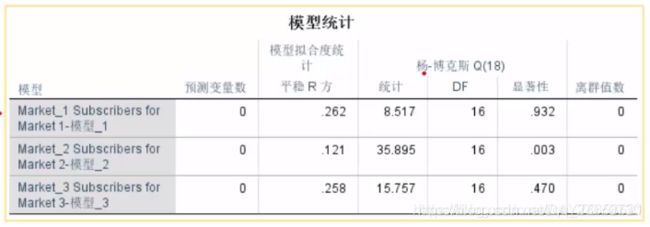
        1）（看“模型统计”表）时间序列的假设检验：通过杨-博克斯模型（Ljung-Box Q(18)），原假设是模型可以很好地拟合原始数据，p>0.05表示模型可以接受，P值越大模型越好。R方值仍然是0~1之间，越大越好。

         2）模型1：

(12个月为一个周期，所以这里是t-12)

        只有当数据窗口中有空的时间数据时，选了预测之后才会有预测结果，不然的话就没有预测。预测结果在输出窗口中，数据窗口中没有。

因果关系ARIMA模型

   1） 操作位置：分析-时间序列预测-创建时间因果模型
   2） 字段窗口：
            目标：因变量，最好选择连续变量
            候选输入：自变量的候选项，有可能是自变量
            目标和输入：选入的变量既是自变量又是因变量
            强制输入：一定需要作为自变量，不管有没有影响

 

3）时间序列因果模型：

     之后再进行拟合，做多元回归线性模型测试

分析-时间序列预测 下的其他几个功能的简介

都用的不太多
交叉相关性

        用来分析不同变量之间是否存在滞后性相关

自相关性

        用来画自相关（ACF）图和偏自相关图。这两个图一般做分析的时候是要画

序列图

        用来画时间序列图

谱图

        用的非常少，但功能很重要，主要用在分析音频上。可以作为第二种判断周期性的方法（第一种是看ACF图）。通过频率取值最高的点对应的频率乘以数据量，得到周期

季节性分解

        一般是在建模前进行的操作，看数据是否在季节上有周期性。不过实用性不强，这一步可以直接交给模型做判断。