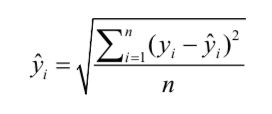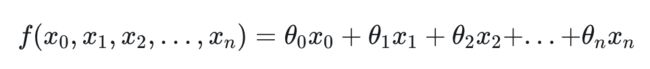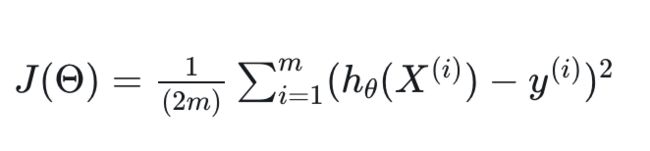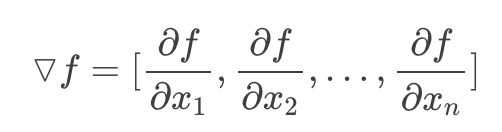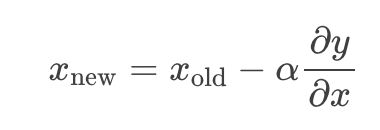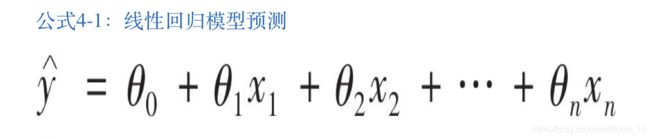机器学习算法/模型——线性回归
线性回归
- 0. 本质和概论
-
- 0.1 本质
- 0.2 概念/术语
- 1. 假设函数
- 2. 损失函数：平方误差函数
- 3. 优化算法
-
- 3.1 梯度下降法：求解函数极值
- 3.2 标准方程（矩阵求解）
- 4.代码实例
-
- 4.1 模型训练
- 4.2 模型可视化（如何将学习好的模型画出来）
- 5. 模型分析与总结
-
- 模型
- 模型参数
- 模型优劣
0. 本质和概论
0.1 本质
线性回归：利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
（最小二乘 = 平方）
概括地说，线性回归模型就是对所有特征添加一个权重，之后求和，最后再添加一个我们称为偏置项的常数，以此进行预测。（瞬间联想到神经网络）
0.2 概念/术语
线性回归模型是：利用线性函数对一个或多个自变量 （x 或 (x1,x2,…xk)）和因变量（y）之间的关系进行拟合的模型。
- 正确理解”线性“：直线、平面…
注意：“线性”的意思并非是 y 和 x 为直线关系！
线性函数的定义是：一阶（或更低阶）多项式，或零多项式。
当线性函数只有一个自变量时，y = f(x)，这里f(x) 的函数形式有三种：
- f(x) = a + bx （a、b 为常数，且 b≠0）—— 一阶多项式；
- f(x) = c (c为常数，且 c≠0) —— 零阶多项式；
- f(x) = 0 —— 零多项式；
但如果有多个独立自变量，y=f(x1,x2,…,xk) 的函数形式则是：
f(x1,x2,…,xk)=a+b1x1+b2x2+…+bkxk
也就是说，只有当训练数据集的特征是一维的时候，线性回归模型可以在直角坐标系中展示，其形式是一条直线。
结论:
特征是一维的，线性模型在二维空间构成一条直线；
特征是二维的，线性模型在三维空间中构成一个平面；
若特征是三维的，则最终模型在四维空间中构成一个体，以此类推。
注：如果不考虑空间维数，这样的线性函数统称为超平面。
注意：特征可以构造，也就是说只有一个特征 x，也可以变为多个：
-
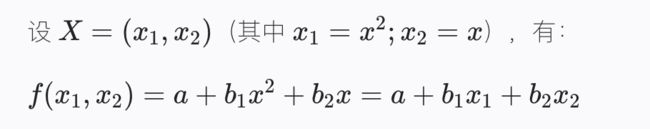
回归
回归分析用于寻找最佳拟合线，使得尽可能多的数据点位于这条线附近（或这条线上）。 -
变量 y ：想要预测的变量
变量 y = 因变量 = 响应变量 = 目标 = 结果 -
自变量：用于预测y的变量
自变量 = 自变量X = 特征 = 属性 -
回归系数：回归线的斜率（一元）
回归系数 = 参数估计值 = 权重 = 斜率（一元）
注：当只存在一个预测变量(x)时，该预测变量的标准化回归系数也被称为相关系数 ，记作 r
-
拟合值：拟合得到的估计值 y ^ \widehat{y} y
拟合值 = 预测值 -
残差：观测值和拟合值之间的差异（真实值−预测值）
残差 = 误差 -
最小二乘法：一种通过最小化残差的平方和而拟合回归的方法。
最小二乘法 = 普通最小二乘法（OLS）
-
均方根误差：回归均方误差的平方根，它是比较回归模型时使用最广泛的度量。
均方根误差 = RMSE
-
标准残差：与均方根误差的计算一样，只是根据自由度做了调整。
标准残差 = RSE
1. 假设函数
通用的线性回归模型，是接受 n 维自变量的。
我们设 x0=1, 因此：
2. 损失函数：平方误差函数
-
平方误差
其中， y ^ \widehat{ y} y i 为第 i 个样本的真实值，yi 为第 i 个样本的预测值。平方误差可能还有一些变种，例如开个根号，除个样本量变成平均值等等。基本上是换汤不换药。 -
目标函数/损失函数
n 维自变量的线性回归模型对应的目标函数就是：
即 预测变量的权重是参数。
3. 优化算法
有梯度下降和标准方程两种方法来求解方程。
3.1 梯度下降法：求解函数极值
梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。
简单地说，梯度下降法先初步猜测合适的权重组合，再通过一个迭代过程，把这些权重应用于每个数据点做预测，然后调整权重，以减少整体预测误差。
注：除了回归之外，梯度下降法也能用来优化其他模型中的参数，比如支持向量机和神经网络。
相关概念:
- 梯度：一阶偏导组成的向量
梯度用 ▽f 来表示，表示函数变化最快的地方
函数f(x1,x2,…,xk) 梯度的定义式，即
- 梯度下降算法的作用/原理
根据导数的正负号，可以判断最小值的坐标是在左边还是右边。
通过导数绝对值的大小，可以判断距离的远近。
用个公式来代替这两条结论的描述，就是
其中，α 是个正数。当 ∂y/∂x>0 时，会得到一个更小的 x，即 x 向左移动。当 ∂y/∂x<0 时，会得到一个更大的 x，即 x 向右移动。且移动的距离 α|∂y/∂x| 与导数的绝对值正相关，满足所有上面的结论。这样，在多次反复使用上面的公式进行循环迭代后，就能逐步逼近函数的极值。
- 梯度下降算法流程：
一句话总结：
从任意点开始，在该点对目标函数求导，沿着导数方向（梯度）“走”（下降）一个给定步长，如此循环迭代，直至“走”到导数为0的位置，则达到极小值。
那么对应的，n 维自变量的线性回归模型对应的目标函数，应用梯度下降，实现的过程是：
3.2 标准方程（矩阵求解）
为了得到使成本函数最小的θ值，有一个闭式解方法——也就是一个直接得出结果的数学方程，即标准方程。
4.代码实例
4.1 模型训练
- 模块导入
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
- 数据准备
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)
- 模型拟合
lin_reg = LinearRegression()
lin_reg.fit(X, y)
- 获取模型参数
print(lin_reg.intercept_, lin_reg.coef_) # Scikit-Learn将偏置项（intercept_）和特征权重（coef_）分离开了
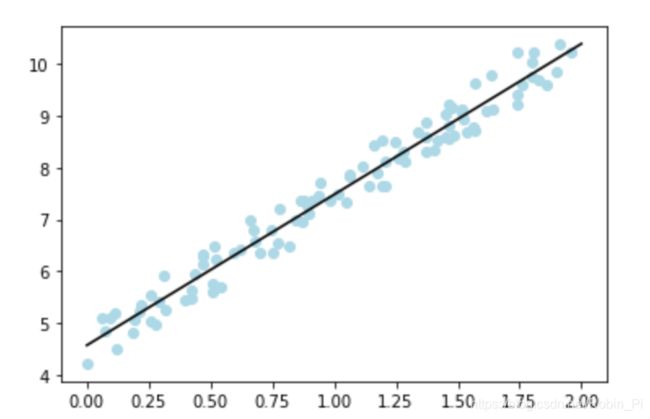
4.2 模型可视化（如何将学习好的模型画出来）
因为学习的是直线方程，所以通过两个新样本来生成模型图像（两点确定一条直线）
注：这里使用的是两个端点值（x 取的是0和2，方便画出完整的直线）
X_new = np.array([[0], [2]])
y_pred = lin_reg.predict(X_new)
y_pred
plt.scatter(X, y, color='lightblue')
plt.plot(X_new, y_pred, 'black')
5. 模型分析与总结
模型
模型参数
- 线性回归主要的参数：权重 θ
- 线性回归的超参数：α
当我们使用梯度下降求解时，梯度下降算法中的步长参数：α，就是训练线性回归模型的超参数。
模型优劣
-
优点
1.简单易用
2.直观 -
劣势
1.对异常值敏感
2.权重失真（含高度相关的变量x）
3.弯曲的趋势
4.并不说明存在因果关系
参考：
- 机器学习必备的数学知识，一次学会
- 机器学习极简入门
- 《白话机器学习》
- 《机器学习实战——基于scikit-learn…》
- 《面向数据科学家的实用统计学》