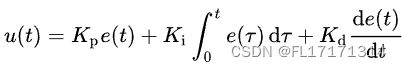机器人PID控制

比例-积分-微分控制器（PID 控制器或三项控制器）是一种采用反馈的控制回路机制，广泛用于工业控制系统和需要连续调制控制的各种其他应用。PID 控制器连续计算误差值 {\displaystyle e(t)}作为所需设定点(SP) 和测量过程变量(PV) 之间的差异，并根据比例、积分和微分项（分别表示为P、I和D）应用校正，因此得名。

积分控制的作用是消除稳态误差，因为系统只要存在误差，积分作用就不断地积累，输出控制量，直到偏差为零，积分作用才会停止。但积分作用太强会使系统超调加大，甚至使系统出现振荡。

实际上，PID 会自动对控制功能进行准确且响应迅速的校正。一个日常的例子是汽车的巡航控制，如果施加恒定的发动机功率，上坡会降低速度。控制器的 PID 算法通过以受控方式增加发动机的功率输出，以最小的延迟和超调将测量速度恢复到所需速度。

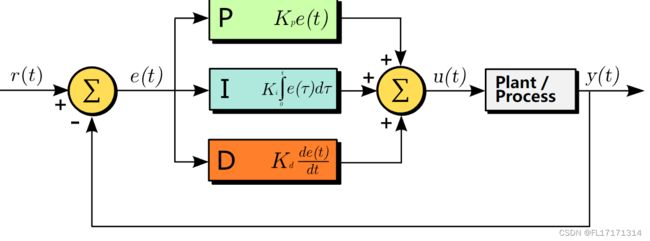
PID控制器的显着特点是能够利用比例、积分和微分这三个控制项对控制器输出的影响来进行精确和优化控制。右侧的框图显示了如何生成和应用这些术语的原理。它显示了一个 PID 控制器，它连续计算一个误差值 {\displaystyle e(t)}作为所需设定点之间的差异 {\displaystyle {\text{SP}}=r(t)}和测量的过程变量 {\displaystyle {\text{PV}}=y(t)}：{\displaystyle e(t)=r(t)-y(t)}, 并根据比例、积分和微分项应用校正。控制器试图通过调整控制变量来使误差随时间最小化 {\displaystyle u(t)}，例如控制阀的开度，到由控制项的加权和确定的新值。

在这个模型中：

• 项P与 SP - PV 误差的当前值成正比{\displaystyle e(t)}. 例如，如果误差较大且为正，则控制输出将成比例地较大且为正，同时考虑到增益因子“K”。单独使用比例控制通常会导致设定点和实际过程值之间出现误差，因为它需要一个误差来生成比例响应。除非存在错误，否则控制器无法调整系统。
• 第I项考虑了 SP - PV 误差的过去值，并随着时间的推移将它们积分以产生第I项。例如，如果在应用比例控制后存在残余 SP - PV 误差，则积分项会通过添加由于误差的历史累积值而产生的控制效果来寻求消除残余误差。当误差消除后，积分项将停止增长。这将导致比例效应随着误差的减小而减小，但这可以通过不断增长的积分效应来补偿。
• D项是基于其当前变化率对 SP − PV 误差未来趋势的最佳估计。它有时被称为“预期控制”，因为它通过施加由误差变化率产生的控制影响来有效地寻求减少 SP - PV 误差的影响。变化越快，控制或阻尼效果就越大。[1]

调谐——这些效果的平衡是通过循环调谐来实现的，以产生最佳控制功能。调谐常数在下面显示为“K”，必须为每个控制应用导出，因为它们取决于控制器外部完整回路的响应特性。这些取决于测量传感器的行为、最终控制元件（例如控制阀）、任何控制信号延迟和过程本身。常数的近似值通常可以在知道应用类型的情况下最初输入，但它们通常通过在实践中通过引入设定点变化和观察系统响应来“冲击”过程来改进或调整。

控制作用——上面的数学模型和实际循环都对所有项使用直接控制作用，这意味着增加的正误差会导致增加的正控制输出校正。如果需要采取消极的纠正措施，则该系统称为反向作用。例如，如果流量回路中的阀门为 0–100% 控制输出的 100–0% 阀门开度 - 意味着控制器动作必须反转。一些过程控制方案和最终控制元素需要这种反向操作。一个例子是冷却水阀门，在信号丢失的情况下，故障安全模式将是阀门 100% 打开；因此 0% 的控制器输出需要导致 100% 的阀门打开。

考虑一个可以通过控制回路移动和定位的机械臂[14] 。电动马达可以提升或降低手臂，具体取决于施加的正向或反向功率，但由于手臂的惯性质量、重力引起的力、手臂上的外力（如负载），功率不能是简单的位置函数举起或在外部物体上做功。

• 感测到的位置是过程变量(PV)。
• 所需位置称为设定点 (SP)。
• PV 和 SP 之间的差异是误差 (e)，它量化了手臂是太低还是太高以及多少。
• 过程的输入（电机中的电流）是 PID 控制器的输出。它被称为操纵变量 (MV) 或控制变量 (CV)。

通过测量位置 (PV) 并将其从设定值 (SP) 中减去，即可找到误差 (e)，控制器从中计算出提供给电机的电流 (MV)。

比例

显而易见的方法是比例控制：电机电流与存在的误差成比例设置。但是，如果手臂必须举起不同的重量，则此方法会失败：对于相同的错误，较大的重量需要施加更大的力，但如果错误较小，则需要较小的力。这就是积分项和导数项发挥作用的地方。

积分

积分项不仅会增加与错误有关的作用，而且还会增加与错误持续时间有关的作用。因此，如果施加的力不足以使误差为零，则该力将随着时间的推移而增加。一个纯粹的“I”控制器可以将错误归零，但它会在开始时反应缓慢（因为动作在开始时会很小，取决于变得重要的时间）和在结束时残酷（动作增加只要误差是正的，即使误差已经开始接近零）。

在误差较小时应用过多的积分并减小会导致超调。超调后，如果控制器要在相反方向上应用较大的修正并反复超调所需位置，则输出将围绕设定点以恒定、增长或衰减的正弦波振荡。如果振荡幅度随时间增加，则系统不稳定。如果它们减少，则系统是稳定的。如果振荡保持在恒定幅度，则系统是边缘稳定的。

导数

导数项不考虑误差的大小（意味着它不能将其归零：纯 D 控制器无法将系统带至其设定点），而是误差的变化率，试图使该速率为零。它旨在将误差轨迹平坦化为一条水平线，抑制施加的力，从而减少超调（由于施加的力太大而导致另一侧的误差）。

 等效地，PID 控制器 的拉普拉斯域中的

传递函数为：

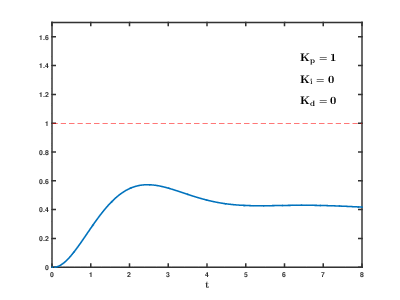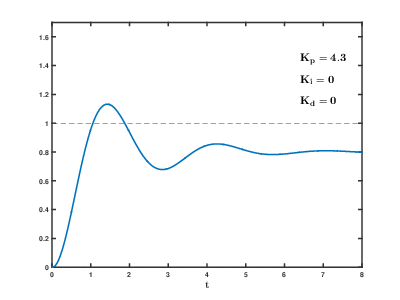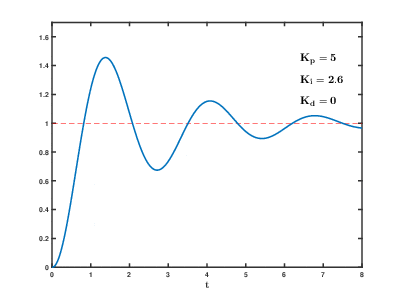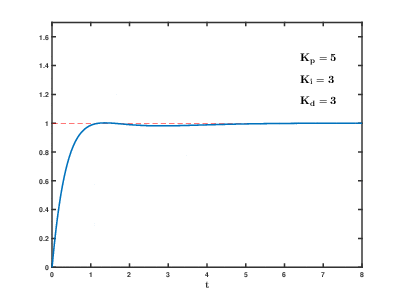
不同 PID 参数 (K p ,K i ,K d ) 对系统阶跃响应的影响：

比例作用： P 作用是与系统的主要响应最相关的组件。增加 P 增益K P 通常会导致更短的上升时间，但也会导致更大的过冲。虽然它可以减少系统的稳定时间，但它也可能导致高度振荡或不稳定的行为。  微分作用：微分作用响应误差信号的变化率，主要与闭环系统的阻尼行为有关。从这个意义上说，增加 D 增益K D通常会导致更小的过冲和更好的阻尼行为，但也会导致更大的稳态误差。

积分作用： 积分作用通常用于优化系统的稳态响应 并塑造其动态行为。 从本质上讲，它为系统带来了内存。 增加 I 增益K I会导致稳态误差减少 （通常消除），但也会导致更多和更大的 振荡。

快速和粗略的调整程序：

• 调整K P 以获得所需的上升时间
• 调整K D以达到所需的设置时间
• 调整K I以消除稳态误差
• 重复和微调

严格的调整方法：

• Ziegler Nichols（经典但不是实现性能的最佳方式）
• 自调整
• 基于线性矩阵不等式和凸优化
• 基于频域

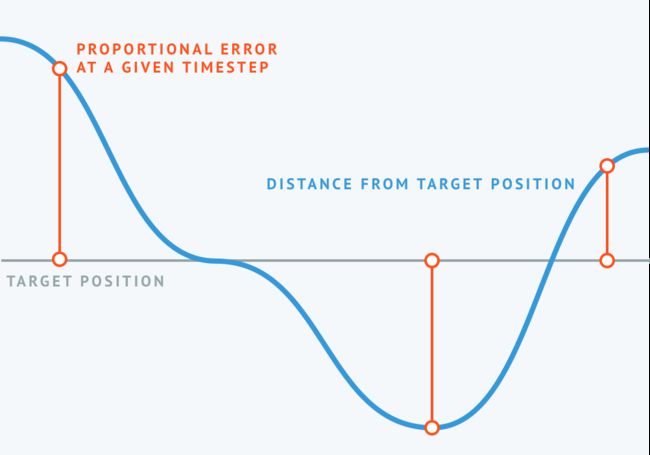
比例响应

比例响应检查当前的误差，因为它从给定时间步按比例评估距离误差。换言之，如果误差量低，则存在小的修正。相反，如果有很多piancha，就会有更大的修正。

想想某人手里拿着的钟摆。当它不静止时，它会前后摆动，因为重力最终总是将钟摆拉回起始位置，其力取决于它与起始位置的距离。当它远离起始位置时，摆锤会以很大的力摆动。

使用比例控制的问题是过冲，即对象过度校正其位置。它类似于摆过静止位置的钟摆。就其本身而言，当物体具有质量或惯性时，比例控制可能会出现问题，因为它们会影响物体的速度，而不管加速物体的任何因素（例如重力或汽车发动机）的影响是否会降低。它没有预料到它会回到目标位置，所以它往往会过冲和振荡。

如果 PC 的增益太高，控制器将不断地在任一方向过度补偿，从而导致明显的振荡。这类似于将汽车从静止位置完全节流，然后当汽车总是超过速度限制时硬制动。

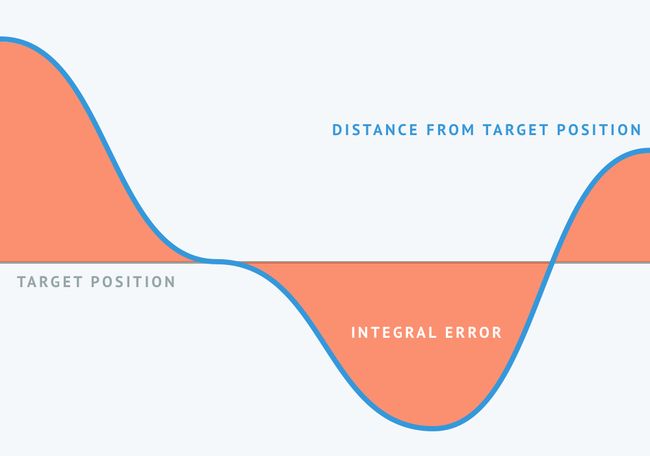
整体反应

积分有助于查看过去的数据，因为它总结了过去的错误。考虑到随着时间的推移没有正确纠正的事实，即使是很小的错误也会导致积分响应逐渐增加。

它对于消除控制系统中的恒定误差很有用，因为无论恒定误差有多小，最终该误差的总和都将足以调整控制器输出。它具有将稳态误差驱动为零的效果。

如果增益太大，控制器可能会变得不稳定，因为正常的控制器波动会被夸大。如果它太小，响应动态变化可能需要很长时间。

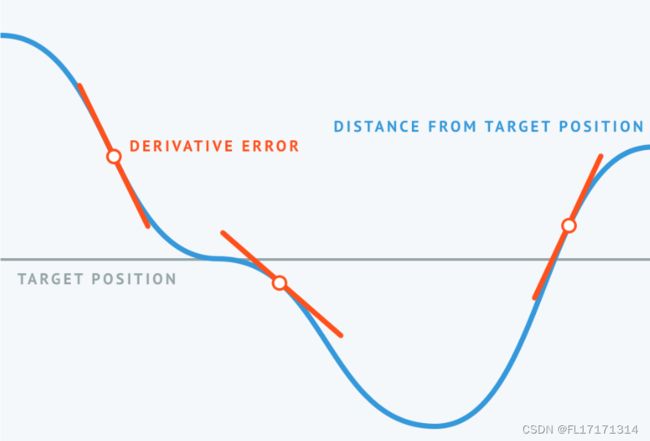
衍生响应

导数响应通过检查在给定时间步造成的误差变化率来预测未来。微分响应与过程变量的变化率成比例。当误差变化缓慢时，导数路径小。误差变化越快，导数路径越大。它有时被称为预期控制。

与比例和积分响应不同，微分响应对稳态误差没有影响。它的作用主要是减少超调。

应用 PID 控制

将这三者放在一起可能是有效的，因为它们可以弥补彼此的不足。

使用案例代码，目标是让机器人通过调整其旋转来沿着设定点行走，因为它在每个时间步都以一致的速度向前行走。在编程方面，我们所要做的就是创建一个运行方法，使用 PID 控制计算转向角。

我们的目标是让机器人将自身重新定位到 0 的位置。这意味着交叉跟踪误差为 y。

积分是所有观察到的误差的总和。导数是当前 y 位置减去先前观察到的 y 位置，除以时间单位1

import random
import numpy as np
import matplotlib.pyplot as plt


# Udacity provided code
class Robot(object):
    def __init__(self, length=20.0):
        """
        Creates robot and initializes location/orientation to 0, 0, 0.
        """
        self.x = 0.0
        self.y = 0.0
        self.orientation = 0.0
        self.length = length
        self.steering_noise = 0.0
        self.distance_noise = 0.0
        self.steering_drift = 0.0

    def set(self, x, y, orientation):
        """
        Sets a robot coordinate.
        """
        self.x = x
        self.y = y
        self.orientation = orientation % (2.0 * np.pi)

    def set_noise(self, steering_noise, distance_noise):
        """
        Sets the noise parameters.
        """
        # makes it possible to change the noise parameters
        # this is often useful in particle filters
        self.steering_noise = steering_noise
        self.distance_noise = distance_noise

    def set_steering_drift(self, drift):
        """
        Sets the systematical steering drift parameter
        """
        self.steering_drift = drift

    def move(self, steering, distance, tolerance=0.001, max_steering_angle=np.pi / 4.0):
        """
        steering = front wheel steering angle, limited by max_steering_angle
        distance = total distance driven, most be non-negative
        """
        if steering > max_steering_angle:
            steering = max_steering_angle
        if steering < -max_steering_angle:
            steering = -max_steering_angle
        if distance < 0.0:
            distance = 0.0

        # apply noise
        steering2 = random.gauss(steering, self.steering_noise)
        distance2 = random.gauss(distance, self.distance_noise)

        # apply steering drift
        steering2 += self.steering_drift

        # Execute motion
        turn = np.tan(steering2) * distance2 / self.length

        if abs(turn) < tolerance:
            # approximate by straight line motion
            self.x += distance2 * np.cos(self.orientation)
            self.y += distance2 * np.sin(self.orientation)
            self.orientation = (self.orientation + turn) % (2.0 * np.pi)
        else:
            # approximate bicycle model for motion
            radius = distance2 / turn
            cx = self.x - (np.sin(self.orientation) * radius)
            cy = self.y + (np.cos(self.orientation) * radius)
            self.orientation = (self.orientation + turn) % (2.0 * np.pi)
            self.x = cx + (np.sin(self.orientation) * radius)
            self.y = cy - (np.cos(self.orientation) * radius)

    def __repr__(self):
        return '[x=%.5f y=%.5f orient=%.5f]' % (self.x, self.y, self.orientation)


def run(robot, tau_p, tau_d, tau_i, n=200, speed=1.0):
    """
    Creates a 2-d trajectory of a robot.
    Arguments:
        tau_p: Float, controls importance of proportionality
        tau_d: Float, controls importance of derivative
        tau_i: Float, controls importance of integral
        n: Integer, number of steps the robot should take.
        speed: Float, how many seconds pass per timestep.
    Returns:
        x_trajectory, y_trajectory: A 2d list containing the
        path taken by the robot.
    """
    x_trajectory, y_trajectory = [], []
    integral = 0.0
    cte = robot.y
    for i in range(n):
        diff = (robot.y - cte) / speed
        cte = robot.y
        integral += cte
        steer = (-tau_p * cte) - (tau_d * diff) - (tau_i * integral)
        robot.move(steer, speed)
        x_trajectory.append(robot.x)
        y_trajectory.append(robot.y)

    return x_trajectory, y_trajectory

机器人从 (x,y) 位置 (0, 1) 开始。目标 y 位置为 0。

使用问题中提供的超参数，该算法几乎收敛于正确的设定点，但我们可以看到它在 -0.03 而不是 0 的 ay 位置附近徘徊。

——————————————————————————————————