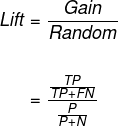机器学习 - 模型评估(TPR、FPR、K1、ROC、AUC、KS、GAIN、LIFT、GINI、KSI)
以下内容多为个人理解,如有不当之处,欢迎指正!
1. 混淆矩阵
一个二分类模型,是对现实情况的一种预测。如病例(阴性/阳性、有病/没病)、邮件(垃圾邮件/非垃圾邮件)等。以病例为例,对于一个患者,存在着有病/没病两种结果。对于医生的诊断,也存在着有病/没病两种结果。将医生的诊断结果与患者的实际情况对比,则得出四种结果:
- 诊断为有病,实际上确实有病,称为真阳性(TP)
- 诊断为有病,实际上却没病,称为伪阳性(FP)
- 诊断为没病,实际上确实没病,称为真阴性(TN)
- 诊断为没病,实际上却有病,称为伪阴性(FN)
将上面的四种结果,可以绘制成一个2x2的混淆矩阵:
| 真实值 | 总数 | |||
| p | n | |||
| 预测输出 | p' | 真阳性(TP) | 伪阳性(FP) | P' |
| n' | 伪阴性(FN) | 真阴性(TN) | N' | |
| 总数 | P | N | ||
需要注意的是,混淆矩阵是对医生的诊断结果(阳性/阴性)以及医生诊断结果的结果(正确/错误)的一种描述,患者的实际患病情况是对医生诊断结果的一种评估。切勿将患者的患病情况与医生的诊断结果的评估混为一谈。即,混淆矩阵是用来评估模型的,而与样本“无关”。
在某一次集体的病例检测的过程中,我们希望尽可能多、尽可能准确的检测出患者。所以,针对这种情况,我们提出以下指标:
1. 准确度(acc, Accuracy):正确诊断为阴性和正确诊断为阳性的占所有样本的比例。
如前所述,我们希望尽可能多、尽可能准确的检测出患者。那么检测出非患者则没有什么意义,因此,准确度并不能很好的反映出我们的目标,或者说并不能衡量出我们预测模型的好坏。甚至如果我们检测出非患者的准确度非常高,反而会影响我们对“尽可能多、尽可能准确的检测出患者”的模型进行评估。
2. 查全率(召回率,Recall):尽可能多反应的是我们希望能够把全部的阳性患者都检测出来。对于医学诊断而言,遗漏下来的患者,可能不能够得到及时的治疗,或者存在更大的隐患(如传染病);或者在图像分类中我们期望尽可能多的把用户期望的类别展现给用户,如用户希望识别小猫的图片,我们可以将图库中更多关于猫的图片展示给用户。那么,查全率表示的就是正确检测为阳性(TP)占全部阳性的概率。其中,全部阳性包括正确检测为阳性(TP),和错误检测为阴性(FN)之和。
3. 查准率(精准率,Precision):尽可能准确反应的是每一个被诊断为阳性的病例都是正确的。类似抢打靶子,枪枪命中,避免子弹的浪费。那么,查准率表示的就是正确检测为阳性(TP)占全部检测为阳性的比例。其中,全部检测为阳性包括正确检测为阳性(TP)和错误检测为阳性(FP)之和。
案例:有200人待检测,其中100人是阳性,100人为阴性(我们并不知道具体是哪个,需要检测出来阳性病例)。
思考以下情况的查全率和查准率
-
只检测1个人,且正确的将其检测为阳性。(查全率:1%,查准率:100%)
-
检测150个人,90人正确检测为阳性,60人错误检测为阳性。(查全率:90%, 查准率:60%)
-
检测200个人,全部将其检测为阳性(100人正确检测为阳性,100人错误检测为阳性)。(查全率:100%, 查准率:50%)
-
检测100个人,全部正确检测为阳性。(查全率:100%,查准率:100%)(理想情况)
通过上面的思考中,我们可以理解,单方面的高查全率或高查准率是没有办法反映出一个预测模型的好坏的,如上述的1、3情况。通常情况下,查全率和查准率率呈现出一种此消彼长的情况。如上述的1、2情况。因此,如何将两个指标融合在一起,更加有效的反应出一个模型的好坏呢?答案是:F1-Score
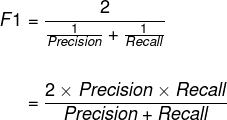
4. F1评分(F1-Score):查全率和查准率的调和平均数。
即:
所谓调和平均数,考虑的是,赋予较小值更大的权重,避免较小值和较大值对结果产生较大影响。对于二分类的情况,则讲究的是不偏科。因为我们追求的就是更高的查全率和更高的查准率,即刚才思考中的情况4。因此F1评分相较于单一的查全率和查准率具备更好的评估效果。
2.ROC曲线和AUC
除了追求的尽可能多、尽可能准确的检测出患者目标。也可以通过另外一个角度来考虑:尽可能多地正确将患者检测为阳性,尽可能少的错误将患者检测为阳性。
真阳性率(TPR,True Positive Rate):也称为命中率 (hit rate)、敏感度(sensitivity),表示正确检测为阳性患者(TP)占全部阳性患者(TP + FN)的比例。我们希望尽可能多地正确将患者检测为阳性,即真阳性率越高越好。
真阳性率与召回率的公式是相同的,因为应用在不同的模型评估指标中,概念有所不同。
伪阴性率(FPR,False Positive Rate):又称错误命中率,假警报率 (false alarm rate),表示错误检测伪阳性患者(FP)占全部阴性患者(FP+TN)的比例。我们希望尽可能少的错误将患者检测为阳性,因此,伪阴性率越低越好。
对于二分类问题,我们所获得的结果往往是通过Sigmoid后映射到[0-1]之间。如以0.5为界限,结果大于0.5,预测为阳性;小于0.5则预测为阴性。类似于考试及格分,100分的考试中,大于60分为及格。将100分映射到[0-1]区间,我们认为大于0.6为及格(即判定为阳性)。那么这个划定阴性/阳性、及格/不及格的界限称为阈值。
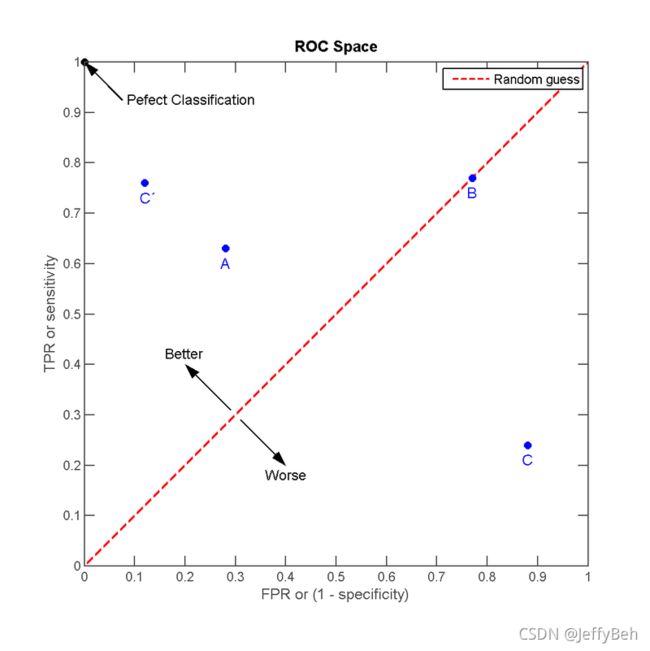
可想而知的是,同样的结果,因为阈值不同,预测的结果也不同。举例说明,王二某次考试为50,如果及格线为60分,则王二为不及格,如果及格线设置为50,则王二及格。对于模型预测也是同理。因为阈值改变而导致的预测结果不同,可以直观的反映到真阳性率和伪阴性率变化上。因此,对于每一个阈值,都对应着一个真阳性率和伪阴性率。我们将伪阴性率作为横轴(X轴),真阳性率作为纵轴(Y轴),来反应这种变化情况。
图片来源:ROC wiki
回归我们的目标:尽可能多地正确将患者检测为阳性,尽可能少的错误将患者检测为阳性。可以知道,我们追求的是更高的TPR和更低的FPR,反映在上图中,则可以理解成越靠近左上角,如A点,分类的效果越好。同理,越靠近右下角,如C点则分类效果越差。对于图中红色的对角线,我们可以看出,TPR和FPR的概率相同,如B点。对于一个样本,检测为阳性正确的概率和错误的概率的是相同的,就是随机预测。最直观的体验就是抛硬币,预测硬币正面朝上(检测为阳性)正确的概率和错误的概率都是50%。
对于对角线右下方的点,如C点,我们只需要做“反向预测”(与对角线对称点,C'),则同样可以获得较好的分类效果。可以理解成,王二做判断题,每次都判断错,那么只要他下次做题的时候,他认为是对的,就判断成错误;他认为吃错的,就判断成正确。那么王二的得分将大大提高。
结合以上,我们将随着阈值变化而变化的真阳性率和伪阴性率所有点描绘出来,则构成一条ROC曲线(receiver operating characteristic curve,接收者操作特征曲线)。
对于一条ROC曲线,因为我们的预测结果区间为[0-1],则阈值的取值范围必然为[0-1]。当阈值取1时,表示没有患者被检测为阳性,则TRP=TP/(TP+FN)中,TP的取值为0;FRP=FP/(FP+TN)中,FP的取值为0,则TPR和FRP均为0。同理,当阈值取0时,TPR和FPR均为1。那么ROC曲线的起点必然是(0, 0),终点必然是(1, 1)。
图片来源:ROC wiki
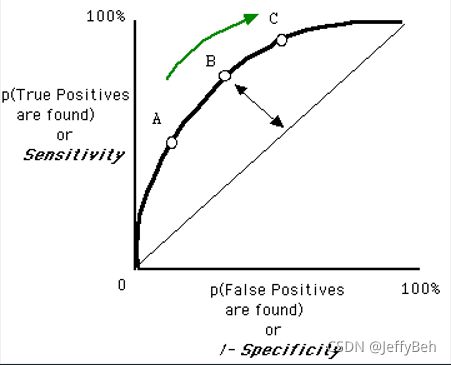
如何通过一条ROC曲线来衡量一个模型的好坏?或如上图中,多条ROC曲线代表的模型的好坏,需要通过什么来衡量呢?答案是:ROC曲线下面积 --AUC(Area under the Curve of ROC (AUC ROC))
从AUC判断分类器(预测模型)优劣的标准:
-
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
-
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设置阈值的话,能有预测价值。
-
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
-
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
注意:AUC是机器学习的社群最常使用来比较不同模型优劣的方法。然而近来这个做法开始受到质疑,因为有些机器学习的研究指出,AUC的杂讯太多,并且很常求不出可信又有效的AUC值,使得AUC在模型比较时产生的问题比解释的问题更多。
3. KS值
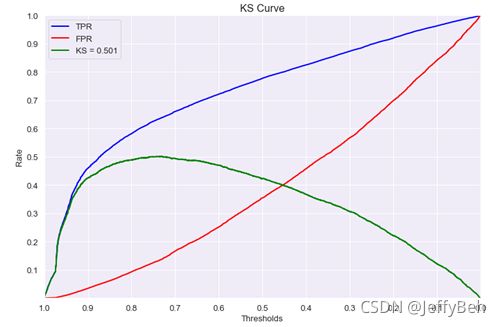
在ROC曲线中,我们将真伪阴性率(FPR)和真阳性率(TPR)分别作为横纵坐标来表示。换一种方式,我们将阈值作为横坐标,将真阳性率和伪阴性率作为纵坐标,在同一个坐标系中,分别画出TPR和FPR随阈值的变化过程。TPR与FPR的最大差值,则被称为KS(Kolmogorov-Smirnov,以发明该指标的两个人命名),即,KS = MAX(TRP - FPR)。
KS值反应的是模型正确区分阳性和阴性样本的能力。取值范围为[0-1](因为TPR和FPR的取值都是[0-1],二者的差值必然也是)。当KS值越大,正确区分阳性和阴性样本的能力越强。
图片来源:深入理解KS
4. GAIN(增益图)和LIFT(提升图)
对于分类问题,我们期望做最少的检测,正确找出最多的阳性样本。
案例分析:在一次样本检测中,共有100个样本,其中20个阳性、80个阴性。
正确检测为阳性的随机概率为20%。即检测10个样本,能够正确检测出2个阳性样本;检测50个样本,能够正确检测出10个。检测100个样本,能够正确检测出20个阳性。而这样的检测效率显然十分低下,我们期望能够使用一个模型,提高准确率。达到做最少的检测,正确找出最多的阳性样本的目标。如,模型的准确率为80%,那么检测10个样本,便能正确检测出8个阳性,那么检测20个样本,就能检测出16个...而通过先验概率来检测,则检测20个样本只能正确检测出4个。两者的差别显而易见。
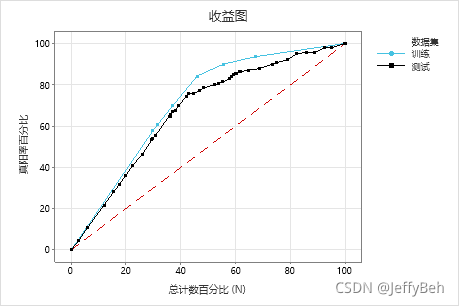
那么,将不同样本区间,正确检测出阳性的比例(即,真阳性率)反映在图中,就是增益图(Gain Charts)。
图片来源:CART® 分类的增益图和提升图
我们知道,随机概率并不会随着样本数量而改变,因此,在图中必然是一条对角线(图中红色虚线)。如检测20个样本,随机概率为20%,那么就会有4个阳性被正确检测出。共有20个阳性样本,则真阳性率为4/20=20%。同理,检测60个样本,则有12个样本被检测出来,真阳性率为12/20=60%。检测100个样本,则真阳性率为100%。
而通过图中蓝色曲线(GAIN)可以看出,当检测60%的样本时,就能够检测出90%多的阳性样本。效率明显高于随机概率。
GAIN图可以直观的反映出利用模型预测与随机概率相比的性能提升效果。
我们进一步将模型训练的真阳性率与随机概率的真阳性率的比例作为衡量利用模型比随机概率的性能提升率的指标,就是提升图(Lift Charts)
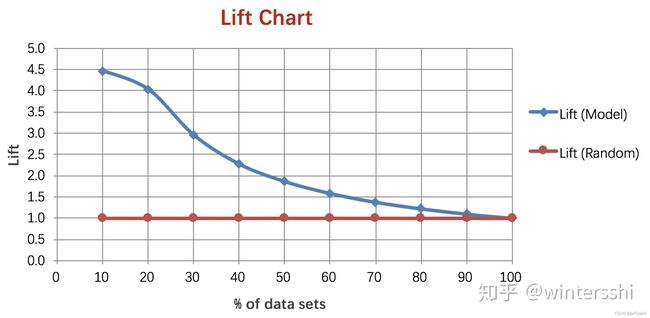
图片来源:ROC、K-S 曲线、Lift 曲线、PR 曲线
图中红色直线可以理解为当模型预测概率是随机概率时,那么Gain=Random,则Lift=Gain/Random=Random/Random=1。以此作为模型Lift衡量基准。
图中蓝色曲线,表示真正的模型预测真阳性率与随机预测的真阳性率的比值。该曲线越陡,即在前面迅速下降,则表示模型的训练效果越好。可以理解为,检测样本较少时,就已经将大部分的阳性样本正确检测出来。
说明:当检测样本时达到100%时,模型预测与随机预测的真阳性率都是100%,二者的比值为1,因此会交于点(100, 1)。
未完待续,近期更新...
以上内容多为个人理解,如有不当之处,欢迎指正!
参考:
ROC曲线
柯尔莫哥洛夫-斯米尔诺夫检验
深入理解KS
KS指标理解