《集体智慧编中文版》读书笔记——第三章：发现群组

前言

发现群组是一个典型无监督学习问题，目的是要在一组数据中找寻某种结构。

关于分级聚类

分级聚类的算法比较简单，主要步骤如下：
1. 从原数据集中挑选最接近的两个样本作为一个组。
2. 生成该组的中心作为一个赝本加入原数据集中。
3. 重复1，直到数据集只有一个样本。
*见clusters.py中的hclustes。
*缺点：（1）、不会真正将数据项拆分成不同组；（2）、必须计算每两个配对项之间的关系，在大规模数据时计算量惊人。

关于K-均值聚类

算法预先告知生成的聚类数量，只需要计算各点与各聚类中心的距离即可。
主要步骤如下：
1. 随机确定k个中心位置。
2. 将个数据项分配给最邻近的中心店。
3. 分配完后，重新计算聚类中心。
4. 重复1。
* 见clusters.py中的kcluster
*缺点：以随机中心点，返回的结果顺序几乎不相同，最终聚类所包含的内容也可能会有所不同。

其他问题

书中还提到两个知识点，第一个，实现起来效果不是很理想，跳过，第二个只是描述双变量相关系数的一种测度方法，不表。

多维压缩：

书中提到的多维压缩即在二维平面上选择代表样本的点，使得各点的直线距离正比于对应样本点的距离指标(这里的距离是认为设定的，比如1-相关系数)

Tanimoto系数：

数据集如果是0，1，表示对应维度特征的有无，可以定义这样的度量相关系数的指标：交集/并集长度之比。

数据集

原文中提取数据的api大部分已失效，这里直接给的博客词类统计表:blogdata.txt。

代码

import clusters as cl

rows = [[1,2,3],[2,3,4],[5,6,7],[4,5,10],[9,10,21],[3,4,8],[7,8,9]]

print('K-均值聚类:')
print(cl.kcluster(rows))

print('分级聚类结果:')
clust = cl.printclust(cl.hclustes(rows))


# 本地（博客 词频 ）表
blogdatapath = r"E:\桌面space\space\学习ing\python学习\集体智慧编程\发现群组\data\blogdata.txt"

# rowsnames 博客名，colnames 词，rows 矩阵
rownames,colnames,rows = cl.readfile(blogdatapath)

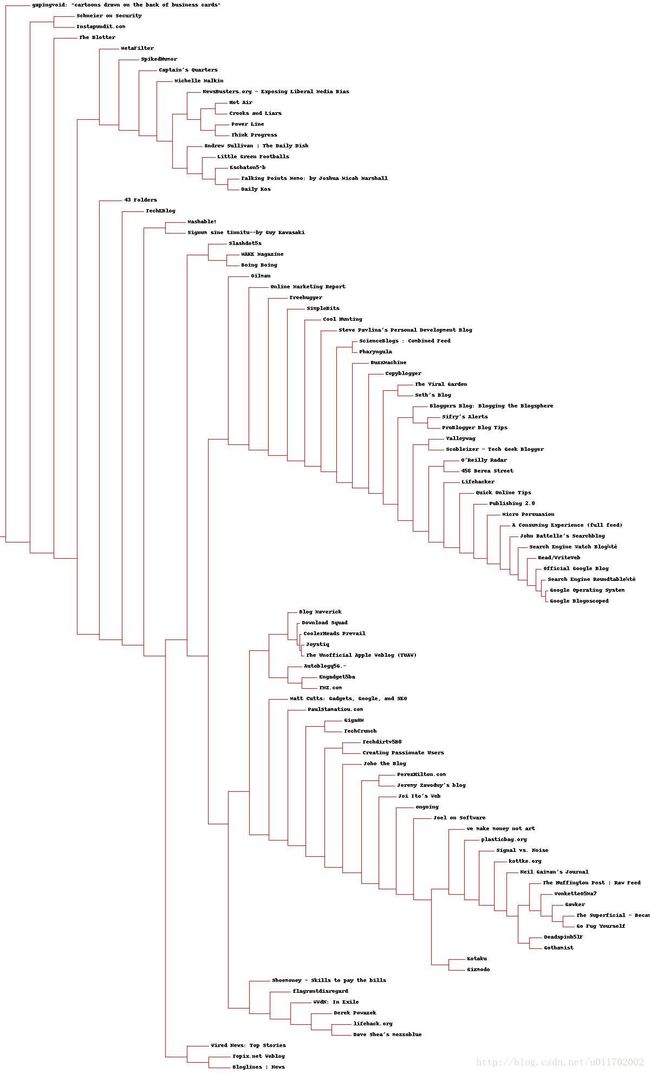
# 分级聚类树状图
clust = cl.hclustes(rows)
cl.drawdendrogram(clust,rownames,
        jpeg = r"E:\桌面space\space\学习ing\python学习\集体智慧编程\发现群组\closests.jpeg")

结果

附件

clusters.py

### 导入博客单词计数表

def readfile(filename):
    lines = [line for line in open(filename)]

    # 第一行是列标题
    colnames = lines[0].strip().split('\t')[1:]

    rownames = []
    data = []
    for line in lines[1:]:
        p = line.strip().split('\t')
        # 每行的第一列是行名
        rownames.append(p[0])

        # 剩余部分就是该行对应的数据

        data.append([float(x) for x in p[1:]])
    return rownames,colnames,data


from math import sqrt


## 皮尔逊相关系数

def pearson(v1, v2):
    sum1 = sum(v1)
    sum2 = sum(v2)

    sq = lambda x : sum([pow(v,2) for v in x])
    sum1sq = sq(v1)
    sum2sq = sq(v2)

    psum = sum([v1[i]*v2[i] for i in range(len(v1))])

    num = psum - (sum1*sum2/len(v1))
    den = sqrt((sum1sq - pow(sum1,2)/len(v1))*(sum2sq - pow(sum2,2)/len(v2)))
    if den == 0 :return 0

    return num/den


### 聚类的类

class bicluster:
    def __init__(self, vec, left = None,right = None,distance = 0, id = None):
        self.vec = vec # 属性数组
        self.left = left # 左节点
        self.right = right # 右节点
        self.id = id # id 小于0时属于分支节点
        self.distance = distance


###  分级聚类

def hclustes(rows,distance = lambda v1,v2 : 1 - pearson(v1, v2)):
    """
        输入：rows 行列矩阵，每一行代表一个对象尸体
              distance 计算距离的函数
        输出：
    """
    distances = {}  # 距离矩阵
    currentclustid = -1 # 标记节点是一个叶子节点

    # 最开始的聚类就是数据集中的行
    clust = [bicluster(rows[i],id = i) for i in range(len(rows))]

    while len(clust)>1:
        lowestpair = (0,1)
        closest = distance(clust[0].vec,clust[1].vec)

        # 遍历每一个配对， 寻找最小距离
        for i in range(len(clust)):
            for j in range(i+1,len(clust)):
                # 用distances来缓存距离的计算值
                if clust[i].id == currentclustid or clust[j].id==currentclustid or (clust[i].id,clust[j].id) not in distances:
                    distances[(clust[i].id,clust[j].id)] = distance(clust[i].vec,clust[j].vec)

                d = distances[(clust[i].id,clust[j].id)]

                if d < closest:
                    closest = d
                    lowestpair = (i,j)

        # 计算两个聚类的平均值
        mergevec = [(v1+v2)/2 for (v1,v2) in zip(clust[lowestpair[0]].vec,clust[lowestpair[1]].vec)]

        newcluster = bicluster(mergevec,left = clust[lowestpair[0]],
                                right = clust[lowestpair[1]],
                                distance = closest,id = currentclustid)
        del clust[lowestpair[1]]
        del clust[lowestpair[0]]
        clust.append(newcluster)
    return clust[0]


### 类似文件系统的方式打印

def printclust(clust, labels=None,n = 1):
    # 利用缩进来建立层级布局
    print(' '*n,end = '')
    if clust.id < 0:
        # 负数代表这是一个分支
        print('-')
    else:
        # 正数代表这是一个叶子节点
        if labels==None:
            print(clust.id)
        else:
            print(labels[clust.id])
    # 现在开始打印右侧分支和左侧分支
    if clust.left!=None:
        printclust(clust.left, labels=labels,n = n+1)
    if clust.right!=None:
        printclust(clust.right, labels=labels,n = n+1)


## 计算聚类树的深度

def getheight(clust):
    # 若是一个叶子节点，高度为1
    if clust.left==None and clust.right==None :return 1

    # 否则，高度为各自之和
    return getheight(clust.left) + getheight(clust.right)


## 横向树相似度只和

def getdepth(clust):
    # 一个叶子节点的距离是0.
    if clust.left==None and clust.right==None:return 0
    # 一个枝节点的距离等于左右两侧分支中距离较大者
    # 加上该枝节点自身的距离
    return max(getdepth(clust.left),getdepth(clust.right)) + clust.distance


from PIL import Image,ImageDraw
## 以树的形式绘制结果

def drawdendrogram(clust, labels=None, jpeg = r'e:\closests.jpg'):
    # 高度和宽度
    h = getheight(clust)*20
    w = 1200
    depth = getdepth(clust)

    # 由于宽度是固定的，因此需要对距离值做相应的调整
    scaling = float(w - 150)/depth

    # 新建一个白色背景的图片
    img = Image.new('RGB', (w,h),(255,255,255))
    draw = ImageDraw.Draw(img)

    draw.line((0,h/2,10,h/2),fill=(255,0,0))

    # 画第一个节点
    drawnode(draw, clust, 10, (h/2), scaling, labels)

    img.save(jpeg,'JPEG')

def drawnode(draw, clust, x, y, scaling, labels):
    if clust.id<0:
        h1 = getheight(clust.left)*20
        h2 = getheight(clust.right)*20
        top = y - (h1+h2)/2
        bottom = y + (h1+h2)/2
        # 线的长度
        l1 = clust.distance*scaling
        # 聚类到其子节点的垂直线
        draw.line((x,top+h1/2,x,bottom - h2/2),fill=(255,0,0))

        # 连接左侧节点的水平线
        draw.line((x,top+h1/2,x+l1,top+h1/2),fill=(255,0,0))

        # 连接右侧节点的水平线
        draw.line((x,bottom - h2/2,x+l1,bottom - h2/2),fill=(255,0,0))

        # 调用函数绘制左右节点
        drawnode(draw,clust.left,x+l1,top+h1/2,scaling,labels)
        drawnode(draw,clust.right,x+l1,bottom-h2/2,scaling,labels)
    else:
        # 如果这是一个叶节点，则绘制节点的标签
        draw.text((x+5,y-7),labels[clust.id],(0,0,0))


### 将行列转置

def rotatematrix(data):
    newdata = []
    for i in range(len(data[0])):
        newrow = [data[j][i] for j in range(len(data))]
        newdata.append(newrow)
    return newdata


### K-均值聚类

import random
def kcluster(rows, distance = lambda v1,v2:1-pearson(v1,v2), k=4):
    # 确定每个维度的最大值和最小值
    ranges = [(min([row[i] for row in rows]),max([row[i] for row in rows])) for i in range(len(rows[0]))]

    # 随机创键k个中心点
    clusters = [[random.random()*(vmax - vmin)+vmin for vmin,vmax in ranges] for j in range(k)]

    lastmatches = None
    for t in range(100):
        # 输出迭代次数
        print('Iteration %d' % t)
        bestmathches = [[] for j in range(k)]

        # 在每一行寻找距离最近的中心点
        for j in range(len(rows)):
            row = rows[j]
            bestmathch = 0
            for i in range(k):
                d = distance(clusters[i], row)
                if d# 如果结果与上次相同， 则整个过程结束
        if bestmathches==lastmatches:break
        lastmatches = bestmathches

        # 把中心点移到其所有成员的平均位置处
        for i in range(k):
            avgs = [0]*len(rows[0])
            if len(bestmathches[i])>0:
                for rowid in bestmathches[i]:
                    for m in range(len(rows[rowid])):
                        avgs[m]+=rows[rowid][m]
                for j in range(len(avgs)):
                    avgs[m]/=len(bestmathches[i])
                clusters[i] = avgs

    return bestmathches


### 多维缩放

def scaledown(data, distance = lambda x,y:1-pearson(x,y), rate = 0.1):
    n = len(data)

    # 每一对数据项之间的真实距离
    realdist = [[distance(data[i], data[j]) for j in range(n)] for i in range(n)]

    outersum = 0.

    # 随机初始化节点在二维空间中的初始位置
    loc = [[random.random(),random.random()] for i in range(n)]
    fakedist = [[0. for j in range(n)] for i in range(n)]

    lasterror = None
    for m in range(1000):
        # 寻找投影后的距离
        # 任意两点的距离fakedist当是两者坐标loc的直线距离
        # for i in range(n):
        #   for j in range(n):
        #       fakedist[i][j] = sqrt(sum([pow(loc[i][x]-loc[j][x],2) for x in range(len(loc[i]))]))

        # 移动节点
        grad = [[0.,0.] for i in range(n)]

        totalerror = 0
        for k in range(n):
            for j in range(n):
                if j==k : continue

                fakedist[j][k] = sqrt(sum([pow(loc[k][x]-loc[j][x],2) for x in range(len(loc[j]))]))
                errorterm = (fakedist[j][k] - realdist[j][k])/realdist[j][k]

                # 每一个节点都需要根据误差的多少，按比例移离或移向其他节点
                grad[k][0] += ((loc[k][0]-loc[j][0])/fakedist[j][k])*errorterm
                grad[k][1] += ((loc[k][0]-loc[j][0])/fakedist[j][k])*errorterm

                # 记录总误差
                totalerror += abs(errorterm)
            loc[k][0] -= rate*grad[k][0]
            loc[k][1] -= rate*grad[k][1]

        # 如果节点移动之后的情况变得更糟，则程序结束
        if lasterror and lasterrorbreak
        lasterror = totalerror

        # 根据rate 参数与grad值相乘的结果，移动每一个节点
        for k in range(n):
            loc[k][0] -= rate*grad[k][0]
            loc[k][1] -= rate*grad[k][1]

    return loc


def draw(data, labels, jpeg = r'E:\桌面space\space\学习ing\python学习\集体智慧编程\发现群组\mds2d.jpg'):
    imgsize = max(100,len(data)*20)
    img = Image.new('RGB',(imgsize,imgsize),(255,255,255))

    draw = ImageDraw.Draw(img)
    for i in range(len(data)):
        x = (data[i][0] + 0.5)*imgsize/2
        y = (data[i][1] + 0.5)*imgsize/2
        draw.text((x,y),labels[i],(0,0,0))
    img.save(jpeg,'JPEG')