【模式识别】C++实现感知器算法
一、问题描述
编写一个感知器算法程序,用此程序求解下列模式分类的解向量:
ω1:{(0 0 0),(1 0 0),(1 0 1),(1 1 0)}
ω2:{(0 0 1),(0 1 1),(0 1 0),(1 1 1)}
设w(1)=(-1 -2 -2 0)
二、算法介绍
对于本次算法程序,我将其分为以下几个部分:
1、变量定义
#define N 100
struct Node //定义了一个用于存放训练样本的数据结构
{
int element[N];//训练样本
int sample;//类别
} node[N];这里定义了一个名为Node数据结构,其中包括两个元素:element(用于记录各个模式类的数据)、sample(用于记录对应数据所属模式类)。
int n;//训练样本的维数
int m;//训练样本的个数
int c;//校正增量系数
Node w[N];//权向量定义了其他所用变量。(注:这里定义的都是全局变量)
2、数据输入部分
cout << "请输入训练样本的维数:";
cin >> n;
cout << "请输入每个训练样本的样本数(这里假设只有两类w1,w2):";
cin >> m;
cout << "请输入训练样本w1:\n";
for (int i = 0; i < m ; i++)
{
for (int j = 0; j < n ; j++)
{
cin >> node[i].element[j];
node[i].sample = 1;
}
}
cout << "请输入训练样本w2:\n";
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cin >> node[m + i].element[j];
node[m + i].sample = 2;
}
}接受用户手动输入的训练样本的维数与个数,用于之后使用(注:这里所用变量n、m均为全局变量)。之后由用户输入训练样本,并将其放在一个名为node的Node类型数组里。(注:在输入训练样本时会同步更新模式类1的sample=1,而模式类2的sample=2,用于在之后使用)
3、规范化处理
Change(node);void Change(Node x[])
{
for (int i = 0; i < 2 * m; i++)
x[i].element[n] = 1;
for (int i = 0; i < 2 * m; i++)
{
for (int j = 0; j <= n; j++)
{
if (x[i].sample == 2)
x[i].element[j] = x[i].element[j] * (-1);
}
}
}调用Change函数将训练样本转化为增广向量的形式,并将属于模式类2的样本乘以-1。
4、初始化权向量与校正增量系数
cout << "请输入初始权向量:\n";
for (int i = 0; i <= n; i++)
{
cin >> w[1].element[i];
}
cout << "请输入校正增量系数:";
cin >> c;接受由用户手动输入的权向量与校正增量系数。
5、迭代计算部分
Preceptron(node, w);void Preceptron(Node x[], Node w[]) //感知器算法
{
int a = 1; //用于记录当前权向量矫正次数
cout << "权向量W(1)为:";
for (int i = 0; i <= n; i++)
{
cout << w[a].element[i] << " ";
}
cout << "\n";
int number = 0; //用于判断是否可以离开迭代循环的变量
while (1)
{
int temp = Mul(w[a], x[(a - 1) % (2 * m)]);
if (temp > 0)
{
number++;
for (int i = 0; i <= n; i++)
{
w[a + 1].element[i] = w[a].element[i];
}
}
else
{
for (int i = 0; i <= n; i++)
{
w[a + 1].element[i] = w[a].element[i] + c * x[(a - 1) % (2 * m)].element[i];
}
}
a++;
cout << "经过调整后的权向量W(" << a << ")为:";
for (int i = 0; i <= n; i++)
{
cout << w[a].element[i] << " ";
}
cout << "\n";
if (a % (2 * m) == 1 && number == (2 * m))//符合退出迭代条件
break;
if (a % (2 * m) == 1)
number = 0;
}
}这里使用了一个名为number的参数用于记录每轮迭代时计算结果大于0的次数,当number与模式类样本个数(2m)相等时(即一轮迭代中并未调整权向量),跳出循环。
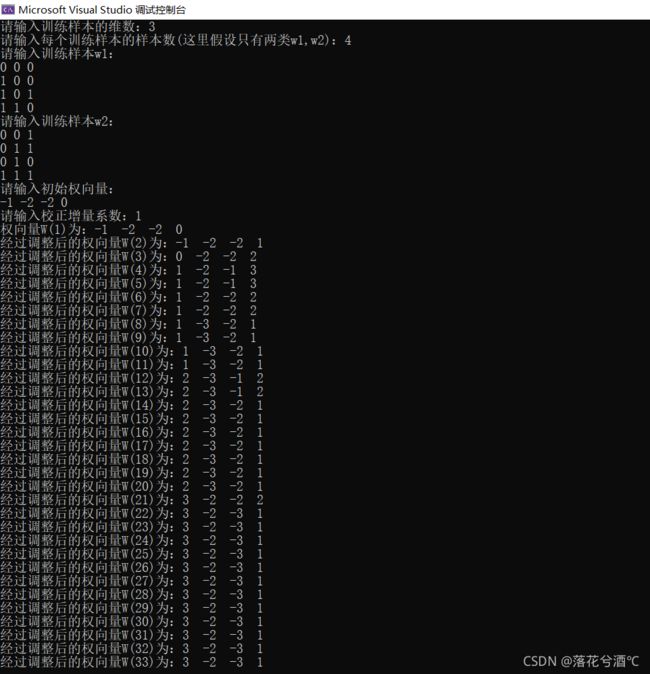
三、计算过程
四、结果图像
五、完整代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define N 100
struct Node //定义了一个用于存放训练样本的数据结构
{
int element[N];//训练样本
int sample;//类别
} node[N];
int n;//训练样本的维数
int m;//训练样本的个数
int c;//校正增量系数
Node w[N];//权向量
void Change(Node x[])
{
for (int i = 0; i < 2 * m; i++)
x[i].element[n] = 1;
for (int i = 0; i < 2 * m; i++)
{
for (int j = 0; j <= n; j++)
{
if (x[i].sample == 2)
x[i].element[j] = x[i].element[j] * (-1);
}
}
}
int Mul(Node a, Node b) //用于实现权向量与训练样本相乘
{
int result = 0;
for (int i = 0; i <= n; i++)
{
result = result + a.element[i] * b.element[i];
}
return result;
}
void Preceptron(Node x[], Node w[]) //感知器算法
{
int a = 1; //用于记录当前权向量矫正次数
cout << "权向量W(1)为:";
for (int i = 0; i <= n; i++)
{
cout << w[a].element[i] << " ";
}
cout << "\n";
int number = 0; //用于判断是否可以离开迭代循环的变量
while (1)
{
int temp = Mul(w[a], x[(a - 1) % (2 * m)]);
if (temp > 0)
{
number++;
for (int i = 0; i <= n; i++)
{
w[a + 1].element[i] = w[a].element[i];
}
}
else
{
for (int i = 0; i <= n; i++)
{
w[a + 1].element[i] = w[a].element[i] + c * x[(a - 1) % (2 * m)].element[i];
}
}
a++;
cout << "经过调整后的权向量W(" << a << ")为:";
for (int i = 0; i <= n; i++)
{
cout << w[a].element[i] << " ";
}
cout << "\n";
if (a % (2 * m) == 1 && number == (2 * m))//符合退出迭代条件
break;
if (a % (2 * m) == 1)
number = 0;
}
}
int main()
{
/*第一步:由用户输入各训练样本的参数*/
cout << "请输入训练样本的维数:";
cin >> n;
cout << "请输入每个训练样本的样本数(这里假设只有两类w1,w2):";
cin >> m;
cout << "请输入训练样本w1:\n";
for (int i = 0; i < m ; i++)
{
for (int j = 0; j < n ; j++)
{
cin >> node[i].element[j];
node[i].sample = 1;
}
}
cout << "请输入训练样本w2:\n";
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cin >> node[m + i].element[j];
node[m + i].sample = 2;
}
}
/*第二步:将输入的训练样本转化为增广向量的形式,并将属于w2的样本乘以-1*/
Change(node);
/*第三步:初始化权向量与校正增量系数*/
cout << "请输入初始权向量:\n";
for (int i = 0; i <= n; i++)
{
cin >> w[1].element[i];
}
cout << "请输入校正增量系数:";
cin >> c;
/*第四步:迭代计算*/
Preceptron(node, w);
return 0;
} 六、备注
本文是感知器算法,使用C++的简单编写,可能有很多不足之处,欢迎讨论