2021年全国研究生数学建模竞赛华为杯D题抗乳腺癌候选药物的优化建模求解全过程文档及程序

2021年全国研究生数学建模竞赛华为杯

D题 抗乳腺癌候选药物的优化建模

原题再现：

  一、背景介绍
  乳腺癌是目前世界上最常见，致死率较高的癌症之一。乳腺癌的发展与雌激素受体密切相关，有研究发现，雌激素受体α亚型（Estrogen receptors alpha, ERα）在不超过10%的正常乳腺上皮细胞中表达，但大约在50%-80%的乳腺肿瘤细胞中表达；而对ERα基因缺失小鼠的实验结果表明，ERα确实在乳腺发育过程中扮演了十分重要的角色。目前，抗激素治疗常用于ERα表达的乳腺癌患者，其通过调节雌激素受体活性来控制体内雌激素水平。因此，ERα被认为是治疗乳腺癌的重要靶标，能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。比如，临床治疗乳腺癌的经典药物他莫昔芬和雷诺昔芬就是ERα拮抗剂。
  目前，在药物研发中，为了节约时间和成本，通常采用建立化合物活性预测模型的方法来筛选潜在活性化合物。具体做法是：针对与疾病相关的某个靶标（此处为ERα），收集一系列作用于该靶标的化合物及其生物活性数据，然后以一系列分子结构描述符作为自变量，化合物的生物活性值作为因变量，构建化合物的定量结构-活性关系（Quantitative Structure-Activity Relationship, QSAR）模型，然后使用该模型预测具有更好生物活性的新化合物分子，或者指导已有活性化合物的结构优化。
  一个化合物想要成为候选药物，除了需要具备良好的生物活性（此处指抗乳腺癌活性）外，还需要在人体内具备良好的药代动力学性质和安全性，合称为ADMET（Absorption吸收、Distribution分布、Metabolism代谢、Excretion排泄、Toxicity毒性）性质。其中，ADME主要指化合物的药代动力学性质，描述了化合物在生物体内的浓度随时间变化的规律，T主要指化合物可能在人体内产生的毒副作用。一个化合物的活性再好，如果其ADMET性质不佳，比如很难被人体吸收，或者体内代谢速度太快，或者具有某种毒性，那么其仍然难以成为药物，因而还需要进行ADMET性质优化。为了方便建模，本试题仅考虑化合物的5种ADMET性质，分别是：1）小肠上皮细胞渗透性（Caco-2），可度量化合物被人体吸收的能力；2）细胞色素P450酶（Cytochrome P450, CYP）3A4亚型（CYP3A4），这是人体内的主要代谢酶，可度量化合物的代谢稳定性；3）化合物心脏安全性评价（human Ether-a-go-go Related Gene, hERG），可度量化合物的心脏毒性；4）人体口服生物利用度（Human Oral Bioavailability, HOB），可度量药物进入人体后被吸收进入人体血液循环的药量比例；5）微核试验（Micronucleus，MN），是检测化合物是否具有遗传毒性的一种方法。
  二、数据集介绍及建模目标
  本试题针对乳腺癌治疗靶标ERα，首先提供了1974个化合物对ERα的生物活性数据。这些数据包含在文件“ERα_activity.xlsx”的training表（训练集）中。training表包含3列，第一列提供了1974个化合物的结构式，用一维线性表达式SMILES（Simplified Molecular Input Line Entry System）表示；第二列是化合物对ERα的生物活性值（用IC50表示，为实验测定值，单位是nM，值越小代表生物活性越大，对抑制ERα活性越有效）；第三列是将第二列IC50值转化而得的pIC50（即IC50值的负对数，该值通常与生物活性具有正相关性，即pIC50值越大表明生物活性越高；实际QSAR建模中，一般采用pIC50来表示生物活性值）。该文件另有一个test表（测试集），里面提供有50个化合物的SMILES式。
  其次，在文件“Molecular_Descriptor.xlsx”的training表（训练集）中，给出了上述1974个化合物的729个分子描述符信息（即自变量）。其中第一列也是化合物的SMILES式（编号顺序与上表一样），其后共有729列，每列代表化合物的一个分子描述符（即一个自变量）。化合物的分子描述符是一系列用于描述化合物的结构和性质特征的参数，包括物理化学性质（如分子量，LogP等），拓扑结构特征（如氢键供体数量，氢键受体数量等），等等。关于每个分子描述符的具体含义，请参见文件“分子描述符含义解释.xlsx”。同样地，该文件也有一个test表，里面给出了上述50个测试集化合物的729个分子描述符。
  最后，在关注化合物生物活性的同时，还需要考虑其ADMET性质。因此，在文件“ADMET.xlsx”的training表（训练集）中，提供了上述1974个化合物的5种ADMET性质的数据。其中第一列也是表示化合物结构的SMILES式（编号顺序与前面一样），其后5列分别对应每个化合物的ADMET性质，采用二分类法提供相应的取值。Caco-2：‘1’代表该化合物的小肠上皮细胞渗透性较好，‘0’代表该化合物的小肠上皮细胞渗透性较差；CYP3A4：‘1’代表该化合物能够被CYP3A4代谢，‘0’代表该化合物不能被CYP3A4代谢；hERG：‘1’代表该化合物具有心脏毒性，‘0’代表该化合物不具有心脏毒性；HOB：‘1’代表该化合物的口服生物利用度较好，‘0’代表该化合物的口服生物利用度较差；MN：‘1’代表该化合物具有遗传毒性，‘0’代表该化合物不具有遗传毒性。同样地，该文件也有一个test表，里面提供有上述50个化合物的SMILES式（编号顺序同上）。
  建模目标：根据提供的ERα拮抗剂信息（1974个化合物样本，每个样本都有729个分子描述符变量，1个生物活性数据，5个ADMET性质数据），构建化合物生物活性的定量预测模型和ADMET性质的分类预测模型，从而为同时优化ERα拮抗剂的生物活性和ADMET性质提供预测服务。
  三、需解决问题
  问题1. 根据文件“Molecular_Descriptor.xlsx”和“ERα_activity.xlsx”提供的数据，针对1974个化合物的729个分子描述符进行变量选择，根据变量对生物活性影响的重要性进行排序，并给出前20个对生物活性最具有显著影响的分子描述符（即变量），并请详细说明分子描述符筛选过程及其合理性。
  问题2. 请结合问题1，选择不超过20个分子描述符变量，构建化合物对ERα生物活性的定量预测模型，请叙述建模过程。然后使用构建的预测模型，对文件“ERα_activity.xlsx”的test表中的50个化合物进行IC50值和对应的pIC50值预测，并将结果分别填入“ERα_activity.xlsx”的test表中的IC50_nM列及对应的pIC50列。
  问题3. 请利用文件“Molecular_Descriptor.xlsx”提供的729个分子描述符，针对文件“ADMET.xlsx”中提供的1974个化合物的ADMET数据，分别构建化合物的Caco-2、CYP3A4、hERG、HOB、MN的分类预测模型，并简要叙述建模过程。然后使用所构建的5个分类预测模型，对文件“ADMET.xlsx”的test表中的50个化合物进行相应的预测，并将结果填入“ADMET.xlsx”的test表中对应的Caco-2、CYP3A4、hERG、HOB、MN列。
  问题4. 寻找并阐述化合物的哪些分子描述符，以及这些分子描述符在什么取值或者处于什么取值范围时，能够使化合物对抑制ERα具有更好的生物活性，同时具有更好的ADMET性质（给定的五个ADMET性质中，至少三个性质较好）。

整体求解过程概述(摘要)

  研究发现，雌激素受体 α 亚型（ERα）是治疗乳腺癌的重要靶标，能够拮抗 ERα 活性的化合物可能是治疗乳腺癌的候选药物。一个化合物想要成为候选药物，除了需要具备良好的生物活性外，还需要在人体内具备良好的药代动力学性质和安全性。通常采用建立化合物生物活性预测模型的方法来筛选潜在活性化合物。本文构建化合物生物活性的定量预测模型和 ADMET 性质的分类预测模型，从而为同时优化 ERα 拮抗剂的生物活性和ADMET 性质提供预测服务。
  本文所做的工作可概括为以下几点:
  问题一：首先通过低方差滤波去除 225 个单一值特征变量，再对剩余的 504 个变量进行灰色关联分析筛选出前 200 名的特征变量，将样本特征比提高至接近 10:1。接着使用基于随机森林的递归特征消除算法选取前 30 名的特征变量，考虑到算法的随机性影响，将算法试验 50 次，对每次选出的 30 个变量计数，最后得到出现频数最高的 30 个变量。因得到的 30 个变量只有计数，没有得分排名，再对选出的 30 个变量做 10 次随机森林回归，取10次回归的平均值作为30个变量最终的相关性得分，选出排名靠前的20个变量。同时，对得分靠前的 20 个变量分别计算其与 pIC50的最大互信息系数得分，距离相关性系数得分，皮尔逊系数得分，验证变量选取的合理性。
  问题二：结合问题 1 递归特征消除选出的和生物活性相关性最高的 30 个特征变量，将变量按对生物活性相关性从高到低排序，求出变量与变量之间的距离相关系数，再通过类似非极大值抑制的方式，对分数高的变量删去和其距离相关系数为强相关的变量(系数>0.6)，从而保证所选变量的独立性，保证选出的特征子集尽可能最优。接着选用 5 种最常用的非线性模型支持向量回归模型，随机森林回归模型，梯度提升回归树模型，XGBoost 模型和 BP 神经网络来建立生物活性预测模型。将 1974 个样本划分成 80%训练集和 20%的测试集，用训练集训练模型，用测试集对模型进行检验，分别得到 5 种模型的三个评价指标 MSE,MAE,^2，通过比对这三个指标，最终确定了拟合优度2为 0.8076 的梯度提升回归树预测模型。使用模型对 test 文件中的 50 个化合物预测 pIC50，并通过 pIC50与IC50之间的转换公式得到 50 个 IC50的结果。
  问题三:首先对每个 ADMET 性质分别进行最优特征子集的选取，每个性质特征子集选取的步骤相同，以 Caco-2 为例，第一步滤去数据集中 225 个单一值特征变量，第二步使用最大互信息系数求取与 Caco-2 相关性最高的 200 个变量，第三步使用基于随机森林的递归特征消除算法选取变量，试验 50 次，每次选出 40 个变量，挑选出现频数大于 40 的特征变量，第四步，按随机森林得分排序变量，第五步使用问题二中提出的类似非极大值抑制的独立性变量剔除算法选出最优的特征子集。得到了 5 个性质各自的特征子集后，选用 5 种分类预测模型，通过在测试集上的准确率比较，确定最终各 ADMET 性质的分类预测模型。一共选出三个支持向量机分类模型和两个 XGBoost 分类模型，使用模型对 test文件中 50 个化合物预测 5 个性质的分类结果。
  问题四：筛选样本数据，分析主要变量分布，选定需要优化的变量。为满足 ADMET 中至少有三个性质较好及各变量上下限的约束条件下，以最大化 pIC50 为目标，建立单目标优化模型。通过差分进化算法求解，得到满足约束条件下的 pIC50 最优解为 9.5537。进行多次迭代，获得的多组最优解差异浮动最大值仅为 2.06%，验证了模型的稳定性和合理性。

模型假设：

  1.假定所有附件中所有提供的数据均为真实数据；
  2.假定数据样本的各个变量数值都在规定的数据范围之内；
  3.假定化合物抑制 ER分子活性除题中所给的分子描述符外，不受外界影响；
  4.假定各分子描述符均可以独立取值。

问题分析：

问题一分析：

  本题的任务为：根据附件二和附件一中提供的数据，针对 1974 个化合物的 729 个分子描述符进行变量选择，并将选出的变量按照重要性程度进行排序，最后给出前 20 个对生物活性最具有显著影响的分子描述符。
  本题主要有以下两个难点：
  难点一：化合物即样本数的个数为 1974 个，变量数即分子描述符的个数为 729 个，样本数量并没有和特征数量拉开一定的差距，在不做任何处理的情况下，若采用基于模型的回归算法进行特征选择易引起严重的过拟合。针对难点一：先对变量进行预筛选，通过方差分析法去除仅有单一值的变量 225 个，再对剩余的 504 个变量进行灰色关联分析，按照关联度进行排序，初步选出前 200 个变量，缓解直接使用回归模型来做特征选择时会产生的过拟合现象。
  难点二：由于目标值生物活性指标 pIC50 与各个变量之间的重要性及相关性并不能直接确定是线性关系还是非线性关系，若二者为非线性关系，可得因、自变量的相关程度低。针对难点二：在灰色关联分析的基础上，为了精准的得到因、自变量的相关程度，本题比对了三类常用的特征选择算法过滤式、包裹式、嵌入式的优缺点，最终选择了包裹式算法基于随机森林回归模型的递归特征消除来选出关联度最高的 30 个变量。由于该算法每次迭代过程时，变量得分会有一定的随机性，将算法试验 50 次，对每次试验选出的变量进行计数，得到了出现频率最高的 30 个变量。最后对第二次筛选后的 30 个变量再做10次随机森林回归，按照得分将30个变量进行排序，最终得出分数最高的20个变量，本题通过多次随机森林以降低平衡算法随机性带来的影响。

问题二分析：

  本题的任务：结合问题 1 的分析，选择不超过 20 个分子描述符，构建化合物对 ERα生物活性的定量预测模型，并使用构建的预测模型对文件“ERα_activity.xlsx”的 test表中的 50 个化合物进行 IC50值和对应的 pIC50值预测。
  本题主要有以下两个难点：
  难点一：题目要求用来拟合预测模型的变量数不能超过 20 个，按照第一问重要性排
序的 20 个变量间可能存在较大的相关性，即 20 个变量之间包含的有用信息较少，建立出
的模型效果会较差。为了使选出用于回归的 20 个变量包含最大的信息量，还需充分考虑
变量之间独立性的影响。
  难点二：由上一章用于模型验证的皮尔森系数可知，各个变量与生物活性指标 pIC50
之间呈线性关系的可能不大，存在高度非线性关系的可能性较大，因此需要选取相应的
非线性模型作为本题生物活性预测模型。

问题三分析：

  本题的任务为：利用 729 个分子描述符，针对 1974 个化合物的 ADMET 数据，分别构建化合物的 Caco-2、CYP3A4、hERG、HOB、MN 性质的分类预测模型，然后使用所构建的 5 个分类预测模型对 test 表中的 50 个化合物进行相应的预测。本题主要有以下两个任务：
  任务一：由于不同的 ADMET 性质存在差异，不能使用同一组特征子集来预测 5 种性质的好坏，各个性质之间需要单独进行特征子集的选择。
  任务二：因为输入特征子集不同，所以需要对每一个性质都单独建立一个二分类预测模型。

问题四分析：

  本题的任务：寻找并阐述化合物的哪些分子描述符，以及这些分子描述符在什么取值或者处于什么取值范围时，能够使化合物对抑制 ERα 具有更好的生物活性，同时具有更好的 ADMET 性质（给定的五个 ADMET 性质中，至少三个性质较好）。
  本题主要有以下难点：
  pIC50的预测模型以及五个 ADMET 的二分类模型为非线性模型，传统的优化算法仅能求出问题的局部最优解，并且求解的结果强烈依赖于初始值。对于此难点，本题采用差分进化算法(Differential Evolution，DE），来进行优化求解，此算法相比传统算法求出全局最优解的可能性更大，但其收敛速度较慢，计算复杂度较高，耗时较长。
  问题四模型分析与求解的思路流程图如图 7.1 所示。

模型的建立与求解

分子描述符变量筛选模型的建立

  本文的分子描述符变量筛选模型建立的研究流程如图 4.1 所示，首先使用低方差滤波法，去除 225 个单一值特征变量；其次，对滤波后的变量候选列表与目标 pIC50 之间进行灰色关联分析(Grey Relation Analysis，GRA)，获取前 200 个与目标关联性最高的主要候选变量，再对这些变量使用基于随机森林的递归特征消除算法 (Recursive feature elimination-Random Forest Regressor, RFE-RF),将算法试验 50 次，对每次试验选出的变量进行计数，得到了出现频率最高的 30 个变量。最后，对这 30 个变量使用随机森林回归试验，得到了重要性前 20 的变量的排序，并对筛选出来的变量以最大互信息系数(Maximal Information Coefficient, MIC)、皮尔森相关系数(Pearson correlation coefficient)、距离相关系数(Distance correlation coefficient)进行合理性验证。
  在得到 504 个分子描述符与 pIC50 的灰色相关性排序后，本题选取前 200 个分子描述符，使用基于随机森林的递归特征消除算法(RFE-RF)对其进一步筛选。递归特征消除主要思想是针对那些特征含有权重的预测模型，RFE 通过递归的方式，不断减少特征集的规模来选择需要的特征。
  第一：给每一个特征指定一个权重，接着采用预测模型在这些原始的特征上进行训练。
  第二：在获取到特征的权重值后，对这些权重值取绝对值，把最小绝对值剔除掉。
  第三：按照这样做，不断循环递归，直至剩余的特征数量达到所需的特征数量。
随机森林是以K个决策树{ℎ(, ), = 1,2, ⋯ , }为基本分类器，进行集成学习后得到的一个组合分类器。当输入待分类样本时，随机森林输出的分类结果由每个决策树的分类结果简单投票决定。这里的{, = 1,2, ⋯ ,}是一个随机变量序列，它是由随机森林的两大随机化思想决定的：
  （1）Bagging思想：从原样本集X中有放回地随机抽取K个与原样本集同样大小的训练样本集{, = 1,2, ⋯ ,}，每个训练样本集构造一个对应的决策树。
  （2）特征子空间思想：在对决策树每个节点进行分裂时，从全部属性中等概率随机抽取一个属性子集(通常取log2() + 1个属性，M为特征总数），再从这个子集中选择一个最优属性来分裂节点。
  训练随机森林的过程就是训练各个决策树的过程，由于各个决策树的训练是相互独立的，因此随机森林的训练可以通过并行处理来实现，这将大大提高生成模型的效率。随机森林中第k个决策树ℎ(, )的训练过程如图4.2所示。将以同样的方式训练得到K个决策树组合起来，就可以得到一个随机森林。当输入待分类的样本时，随机森林输出的分类结果由每个决策树的输出结果进行简单投票（即取众数）决定。随机森林分类流程如图4.3所示。

  随机森林对噪声和异常值有较好的容忍性，能够在不需要降维的条件下处理具有高维特征的输入样本，而且能够评估各个特征在分类问题上的重要性，具有良好的可扩展性和并行性。
  随机森林算法可以在分类的基础上进行回归分析，通过将样本分类的结果进行一定的运算可以获得各个分子描述符的重要性，表示各分子描述符对预测pIC50的影响程度，某一分子描述符重要性越大，表明该分子描述符对预测pIC50的影响越大，重要性越小，表明该分子描述符对预测pIC50的影响越小。随机森林算法中某一特征的重要性，是该特征在内部所有决策树重要性的平均值，而在决策树中，计算某一个特征的重要性可以采用以下方法：


  最终得到这 200 个分子描述符对预测 pIC50的重要性排序，进行递归消除。由于随机森林每颗树的训练样本是随机的，树中每个节点的分裂属性集合也是随机选择确定的，导致此算法结果具有一定的随机性，为了尽可能平衡此随机性对结果的影响，本题将对这 200 个特征进行五十次 RFE-RF 算法，对每次试验选出的特征进行计数，得到了出现频率最高的 30 个特征。
  最后，本题对这 30 个特征进行了 10 次基于随机森林的重要性排序，取其平均值得到前 20 个对 pIC50影响最大的特征及其排序。基于随机森林的 RFE 在本文中的实现可概括如图 4.4 所示。

  使用 Python 编程实现方差分析，在这里只去除单一值特征变量，总计 225 个，部分要删除的变量名称如表 4.1 所示：

  本题对剩余 504 个变量使用 Python编程实现灰色关联分析，选出前 200 个特征变量，算法参数：分辨系数值选择为 0.5。灰色关联分析得分情况如表 4.2 所示：

  由上表可知：当分辨系数值选择为 0.5，灰色关联得分的最大值和最小值之间的差距在 0.3，第一名和第 200 名的得分差距在 0.23，后面从 201 名到最后 504 名的得分差距在0.068，可以很明显的看出对生物活性影响较大的分子描述符变量在前 200 名内。

基于随机森林的递归特征消除

  由于递归特征消除的特征选择结果具有一定的随机性，本题对灰色关联分析得到的前200 名的特征做 50 次递归特征消除算法试验，每次试验输出 30 个特征变量，对每次试验出现的特征进行计数，选取前 30 个出现频数最高的特征，各变量出现的频数如图 4.4 所示。

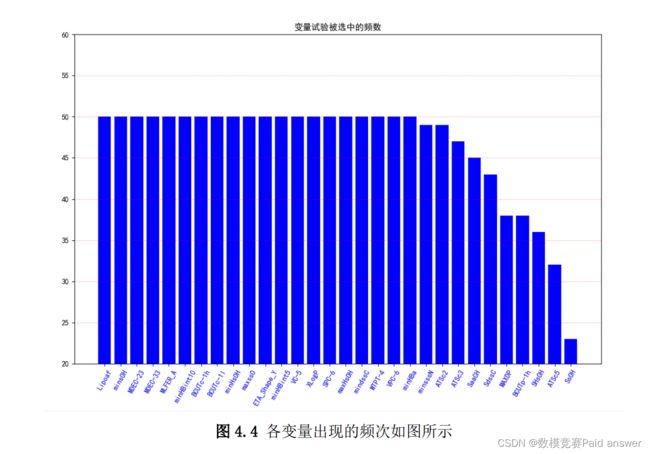
  使用 Python 编程实现递归特征消除试验，具体参数设置见表 4.3 所示：

随机森林回归重要性排序

  由于算法递归特征消除可以较准确的得到与生物活性相关性大的特征变量，但其无法对所得的 30 个变量按照重要性进行排序。为此通过对 30 个变量再做随机森林回归，得到 30 个变量的重要性排序。考虑到随机森林算法结果同样具有一定的随机性，通过试验10 次，对 10 次结果取平均值，得到最终要求的前 20 个分子描述符，具体结果如表 4.4 所示。

合理性验证

  为了验证特征筛选的合理性及其重要性排名的可靠性，本题使用最大互信息系数(MIC)、距离相关系数、皮尔森系数的方法来对本题确定的 20 个按重要性排序的变量进行合理性验证，结果如表 4.5 所示。

  综合表 4.4、表 4.5 和图 4.4 可以看出 20 个特征在几种衡量特征重要性的评价方法下的异同。可以得到如下规律:
  (1)互信息—最大信息数 MIC、距离相关系数、基于随机森林回归的特征重要性排序较为相近，体现了主要变量在不同规则下的平稳度；
  (2)此 20 个特征与生物活性之间的距离相关系数和最大信息数 MIC 都较大，体现了其都对目标影响较大，验证了本题变量选择的合理性。
  (3)Pearson 相关系数得分中所有变量得分的绝对值都未超过 0.6，可得这些特征与生物活性的线性相关性比较低，所以预测 pIC50时更适合使用非线性的回归模型进行预测。

生物活性预测模型的建立

  本题模型建立及求解的流程图如图 5.1 所示，首先选取和生物活性相关性最高的 30个特征变量，求出他们之间的距离相关系数，再通过类似非极大值抑制的方式，将变量按它们对生物活性相关性从高到低排序，对分数高的变量删去和他们距离相关系数为强相关的变量，从而保证所选变量的独立性，保证选出的特征子集含有最大的信息量。解决完变量的独立性问题后，选用 5 种最常用的非线性模型：支持向量回归模型，随机森林回归模型，梯度提升回归树模型，XGBoost 模型和 BP 神经网络来建立生物活性预测模型。将 1974 个样本划分成 80%训练集和 20%的测试集，用训练集训练，用测试集对 5种非线性模型进行检验，分别得到 5 种模型的三个评价指标 MSE,MAE,2，通过对比这三个指标，选取最终的生物活性 pIC50预测模型。

变量独立性剔除算法的建立

在统计学中，对相关性强弱有如下约定，如表 5.1 所示。

  为了保证变量之间的独立性，本题的首要目标是得到一特征子集，使特征变量之间的相关性小于 0.6。
  为此，本题首先选取第一问按随机森林得分排序后的 30 个变量，计算 30 个变量两两之间的距离相关系数，使用类似非极大值抑制的方式对 30 个变量进行变量剔除，剔除的阈值选择为 0.6，具体算法流程如图 5.2 所示。

梯度提升回归树模型的建立

  本题使用梯度提升回归树模型作为第四个非线性生物活性预测模型。GBDT模型是Boosting算法的一种，也是Boosting算法的一种改进。他传统的Boosting有着很大的区别，GBDT的核心就在于每一次计算都是为了减少上一次的残差（Residual），而为了减少这些残差，可以在残差减少的梯度（Gradient）方向上建立一个新模型。在GBDT中，每个新模型的建立是为了使得先前模型残差往梯度方向减少，与传统Boosting算法对正确、错误的样本进行加权有着极大的区别。

论文缩略图：

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

#距离相关系数筛选部分
import dcor
test_data=n1.iloc[:,1:]
Y_data=np.array(n1['y'].tolist())
score_list=[]
for col in test_data.columns:
x=test_data[col]
score=dcor.distance_correlation(x,Y_data)
score_list.append(score)
score_list
#基于随机森林的单变量打分
from sklearn.model_selection import cross_val_score,
ShuffleSplit
from sklearn.ensemble import RandomForestRegressor
import numpy as np
X = n2.iloc[:,1:]
Y = n2['y'].tolist()
names = n2.columns.tolist()[1:]
rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
# 单独采用每个特征进行建模，并进行交叉验证
for i in range(X.shape[1]):
score = cross_val_score(rf, X.iloc[:, i:i+1], Y,
scoring="r2",cv=ShuffleSplit(len(X), 3, .3))
scores.append((format(np.mean(score), '.3f'), names[i]))
print(sorted(scores, reverse=True))
name_list3=[]
score_list3=[]
for index in scores:
name_list3.append(index[1])
score_list3.append(index[0])
final_re=pd.DataFrame({'col':name_list3,'score':score_list3})
#GBDT部分
rfc_s_list=[]
list_nes=list(range(240,300))
for i in list_nes:
clf =
GradientBoostingRegressor(n_estimators=i,max_depth=3,loss='ls')
rfc_s =
cross_val_score(clf,x_train,y_train,cv=10,n_jobs=-1).mean()
rfc_s_list.append(rfc_s)
print(max(rfc_s_list),
list_nes[rfc_s_list.index(max(rfc_s_list))])
plt.plot(list_nes,rfc_s_list)
plt.show()
rfc_m_list=[]
list_nes=list(range(1,14))
for i in list_nes:
clf =
GradientBoostingRegressor(n_estimators=295,max_depth=i,loss='ls')
rfc_s =
cross_val_score(clf,x_train,y_train,cv=10,n_jobs=-1).mean()
rfc_m_list.append(rfc_s)
print(max(rfc_m_list),
list_nes[rfc_m_list.index(max(rfc_m_list))])
plt.plot(list_nes,rfc_m_list)
plt.show()
rfc_su_list=[]
list_nes=[0.6,0.7,0.8,0.9,1]
for i in list_nes:
clf =
GradientBoostingRegressor(n_estimators=295,max_depth=5,loss='ls',subsample=i)
rfc_s =
cross_val_score(clf,x_train,y_train,cv=10,n_jobs=-1).mean()
rfc_su_list.append(rfc_s)
print(max(rfc_su_list),
list_nes[rfc_su_list.index(max(rfc_su_list))])
plt.plot(list_nes,rfc_su_list)
plt.show()
clf=GradientBoostingRegressor(n_estimators=295,max_depth=5,loss='ls',subsample=0.7)
clf.fit(x_train,y_train)
predict_x3=clf.predict(x_test)
print(r2_score(predict_x3,y_test))
import matplotlib.pyplot as plt
plt.figure(figsize=[15,8])
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.scatter(range(0,len(predict_x3)),predict_x3,c='b',marker='*',s=80,label="预测值")
plt.scatter(range(0,len(y_test) ),y_test,c =
'r',s=80,marker='o',label="真实值")
plt.legend(['真实值','预测值'],loc = 1,fontsize = 6)
plt.xlabel('样本个数',fontsize = 15)
plt.ylabel('值',fontsize = 15)
plt.legend(fontsize='xx-large')
plt.title('R^2=0.7235',fontsize = 20)
# plt.text(480,3,'R^2=0.7235')
plt.savefig(r'C:\Users\Admin\Desktop\202\2021年D题\基于RFE
GBDT对试验样例的预测结果.png')
plt.show()
#集成学习部分
from sklearn.model_selection import cross_val_score
#创建数据集
dataset = Dataset(x_train,y_train,x_test)
model_rf=Regressor(dataset=dataset,estimator=RandomForestRegressor,parameters={'n_estimators':
108,'max_depth':20},name='rf')
#model_lr=Regressor(dataset=dataset,estimator=LinearRegression,
parameters={'normalize': True},name='lr')
#model_rfc=Regressor(dataset=dataset,estimator=SVR,parameters={'kernel':'rbf','gamma':0.4683673469387755,'C':3.787878787878788,'epsilon':0.1,'cache_size':5000},name='svr')
#model_dtr=Regressor(dataset=dataset,estimator=DTR,parameters={'max_depth':4},name='dtr')
model_xgb=Regressor(dataset=dataset,estimator=XGBRegressor,parameters={'learning_rate':0.1,'n_estimators':139,'max_depth':5,'min_child_weight':3,'gamma':0.02,'subsample':0.8,'colsample_bytree':0.7,'reg_alpha':1,'objective':'reg:linear'},name='xgb')
model_gbdt=Regressor(dataset=dataset,estimator=GradientBoostingRegressor,parameters={'n_estimators':295,'max_depth':5,'loss':'ls'},name='gbdt')
# Stack two models
# Returns new dataset with out-of-fold predictions
pipeline = ModelsPipeline(model_rf,model_xgb,model_gbdt)
stack_ds = pipeline.stack(k=10,seed=111)#用于stacking
# Train LinearRegression on stacked data (second stage)
stacker = Regressor(dataset=stack_ds,
estimator=GradientBoostingRegressor)
results4 = stacker.predict()
# Validate results using 10 fold cross-validation
result = stacker.validate(k=10,scorer=r2_score)
#xgboost部分
param =
{'silent':True,'obj':'reg:linear',"subsample":0.8,"max_depth":5,"eta":0.1,"gamma":0.02,"lambda":1,"alpha":0,"colsample_bytree":0.8,"colsample_bylevel":1,"colsample_bynode":1,"nfold":5}
num_round = 139
model = xgb.train(param, dfull, num_round)
from sklearn.metrics import r2_score
dtest = xgb.DMatrix(x_test)
r2_score(y_test,model.predict(dtest))
#汇总综合图部分
import matplotlib.pyplot as plt
xx=range(0,len(y_test))
plt.figure(figsize=(20,8))
plt.scatter(xx,y_test,color="#000080",label="Sample
Point",linewidth=3)
plt.plot(xx,results4,color="#4876FF",label="FittingLine_Integratedlearning",linewidth=1)
plt.plot(xx,y_hat2,color="#A2CD5A",label="FittingLine_RF",linewidth=1)
plt.plot(xx,predict_x3,color="#FFFF00",label="FittingLine_GBDT",linewidth=1)
plt.plot(xx,predict_y,color="#FF6A6A",label="FittingLine_XGB",linewidth=1.5)
plt.rcParams.update({'font.size': 12})
plt.legend(loc='upper left')
plt.legend()
plt.savefig(r'C:\Users\Admin\Desktop\202\2021年D题\基于RFE
横向对比.png')
plt.show()
#分布图部分
sp=oridata.corr('spearman')
fig_path='./随机森林打分+xgboost拟合结果图.png'
fig=sns.pairplot(sp)
scatter_fig = fig.get_figure()
scatter_fig.savefig(fig_path, dpi = 400)
#热力图部分
import seaborn as sns
import palettable
import matplotlib as mpl
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(11, 9),dpi=100)
fig=sns.heatmap(data=sp,vmax=1,
cmap=palettable.cmocean.diverging.Curl_10.mpl_colors,
# annot=True,
# fmt=".2f",
annot_kws={'size':8,'weight':'normal',
'color':'#253D24'},
mask=np.triu(np.ones_like(sp,dtype=np.bool)),#显示对脚线下面部分图
square=True,
linewidths=.5,#每个方格外框显示，外框宽度设置
cbar_kws={"shrink": .5}
)
scatter_fig = fig.get_figure()
#低方差滤波部分
Y_data=np.array(data_selected['pIC50'].tolist())
score_list=[]
for col in test_data.columns:
x=test_data[col]
score=dcor.distance_correlation(x,Y_data)
score_list.append(score)
score_list
#t-sne可视化部分
# #二维空间
ts = TSNE(n_components=2, init= 'pca' , random_state=3)
reslut = ts.fit_transform(need_data_norm)
plt = plot_embedding(reslut, labels2, 't-SNE Embedding of
digits' )
plt.xlabel('x')
plt.ylabel('y')
plt.title('t-sne聚类结果二维可视化')
plt.savefig('./t-sne聚类结果二维可视化.png')
plt.show()
# 2.绘制图片
plt.figure("三维空间的映射",figsize=[8,8], facecolor="lightgray")
ax3d = plt.gca(projection="3d") # 创建三维坐标
# ax3d.view_init(elev=70, azim=30)
ax3d.view_init(elev=45, azim=30)
#三维
plt.title('三维空间的映射', fontsize=18)
ax3d.set_xlabel('x', fontsize=20)
ax3d.set_ylabel('y', fontsize=20)
ax3d.set_zlabel('z', fontsize=20)
plt.tick_params(labelsize=10)
ax3d.set_xticks(ra)
ax3d.scatter(x, y, z, s=30, c=labels, cmap="Set1", marker="o")
plt.show()
#遗传算法特征选择部分
X=need_data
y=yy.iloc[:,0].tolist()
estimator = RFC(n_estimators=30)
model = GeneticSelectionCV(
estimator, #模型
cv=5, #交叉验证
verbose=0,
scoring="accuracy",#评价标准
max_features=25,#最多模型特征
n_population=100, #种群大小
crossover_proba=0.5,#交叉概率
mutation_proba=0.2, #变异概率
n_generations=50,#迭代次数
crossover_independent_proba=0.5,
mutation_independent_proba=0.04,
tournament_size=3,
n_gen_no_change=10,
caching=True,
n_jobs=-1)
model = model.fit(X, y)
print('Features:', X.columns[model.support_])
#递归特征删除部分
score_list=[]
for index in range(7,26):
RFR_ = RandomForestClassifier(n_estimators=30)
selector1 = RFE(RFR_, n_features_to_select=index,
step=1).fit(X, Y) #
n_features_to_select表示筛选最终特征数量，step表示每次排除一个特征
# selector1.support_.sum() # 选择特征数量
X_wrapper1 = selector1.transform(X) #
最优特征，返回的是筛选后的自变量
score =cross_val_score(RFR_, X_wrapper1, Y, cv=9).mean()
print(score)#对筛选后的指标进行随机森林回归的交叉验证的得分
print("Support is %s" % selector1.support_) # 是否保留
score_list.append([index,score,selector1.support_])
score_list
import xgboost as xgb
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def schaffer(x):
x1, x2, x3 ,x4,x5, x6, x7 ,x8,x9, x10, x11 ,x12,x13, x14,
x15 ,x16,x17, x18, x19, \
x20, x21, x22 ,x23,x24, x25, x26 ,x27, x28, x29, x30
,x31,x32, x33, x34 ,x35,x36, x37, x38 ,x39, \
x40, x41, x42 ,x43,x44, x45, x46 ,x47, x48, x49, x50
,x51,x52, x53, x54 ,x55 = x
reward = 0
temp1 = pd.DataFrame(index=needed1.columns,data =[x19, x14,
x55, x12, x41, x4, x11, x6, x20, x26, x18, x34, x51, x22,
x47,
x33, x45,x29, x16, x17, x35,
x53])
xgbtemp1 = xgb.DMatrix(temp1.T)
key1 = model1.predict(xgbtemp1)
key_predictions1 = [round(value) for value in key1][0]
if key_predictions1 == 1:
reward = reward+1
temp2 = pd.DataFrame(index=needed2.columns,data =[x28, x40,
x37, x42, x38, x27, x30, x8, x6, x44, x15, x13, x22, 23])
xgbtemp2 = xgb.DMatrix(temp2.T)
key2 = model2.predict(xgbtemp2)
key_predictions2 = [round(value) for value in key2][0]
if key_predictions2 == 1:
reward = reward+1
temp3 = pd.DataFrame(index=needed3.columns,data =[x36, x21,
x4, x44,x41, x52, x46])
xgbtemp3 = xgb.DMatrix(temp3.T)
key3 = model3.predict(xgbtemp3)
key_predictions3 = [round(value) for value in key3][0]
if key_predictions3 == 0:
reward = reward+1
temp4 = pd.DataFrame(index=needed4.columns,data =[x3, x25,
x49, x32, x38, x39, x31])
xgbtemp4 = xgb.DMatrix(temp4.T)
key4 = model4.predict(xgbtemp4)
key_predictions4 = [round(value) for value in key4][0]
if key_predictions4 == 1:
reward = reward+1
temp5 = pd.DataFrame(index=needed5.columns,data =[x50, x43,
x5, x54, x1, x10, x2, x24, x7, x9, x48])
xgbtemp5 = xgb.DMatrix(temp5.T)
key5 = model5.predict(xgbtemp5)
key_predictions5 = [round(value) for value in key5][0]
if key_predictions5 == 0:
reward = reward+1
return -reward
from sko.GA import GA
ga = GA(func=schaffer, n_dim=55, size_pop=100, max_iter=80,
prob_mut=0.001, lb=ll, ub=uu,
precision=pre)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', -best_y)
f =[]
def func(x):
x1, x2, x3 ,x4,x5, x6, x7 ,x8,x9, x10, x11 ,x12,x13, x14,
x15 ,x16,x17, x18, x19, x20= x
temp = pd.DataFrame(index=X.columns,data = [x1, x2, x3
,x4,x5, x6, x7 ,x8,x9, \
x10, x11 ,x12,x13, x14, x15
,x16, x17,\
x18, x19 ,x20])
key1 = model1.predict(xgbtemp1)
key_predictions1 = [round(value) for value in key1][0]
if key_predictions1 == 1:
reward = reward+1
temp2 = pd.DataFrame(index=needed2.columns,data =[x28, x40,
x37, x42, x38, x27, x30, x8, x6, x44, x15, x13, x22, 23])
xgbtemp2 = xgb.DMatrix(temp2.T)
key2 = model2.predict(xgbtemp2)
key_predictions2 = [round(value) for value in key2][0]
if key_predictions2 == 1:
reward = reward+1
temp3 = pd.DataFrame(index=needed3.columns,data =[x36, x21,
x4, x44,x41, x52, x46])
xgbtemp3 = xgb.DMatrix(temp3.T)
key3 = model3.predict(xgbtemp3)
key_predictions3 = [round(value) for value in key3][0]
if key_predictions3 == 0:
reward = reward+1
temp4 = pd.DataFrame(index=needed4.columns,data =[x3, x25,
x49, x32, x38, x39, x31])
xgbtemp4 = xgb.DMatrix(temp4.T)
key4 = model4.predict(xgbtemp4)
key_predictions4 = [round(value) for value in key4][0]
if key_predictions4 == 1:
reward = reward+1
temp5 = pd.DataFrame(index=needed5.columns,data =[x50, x43,
x5, x54, x1, x10, x2, x24, x7, x9, x48])
xgbtemp5 = xgb.DMatrix(temp5.T)
key5 = model5.predict(xgbtemp5)
key_predictions5 = [round(value) for value in key5][0]
if key_predictions5 == 0:
reward = reward+1
return -reward
from sko.GA import GA
ga = GA(func=schaffer, n_dim=55, size_pop=100, max_iter=80,
prob_mut=0.001, lb=ll, ub=uu,
precision=pre)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', -best_y)
f =[]
def func(x):
x1, x2, x3 ,x4,x5, x6, x7 ,x8,x9, x10, x11 ,x12,x13, x14,
x15 ,x16,x17, x18, x19, x20= x
temp = pd.DataFrame(index=X.columns,data = [x1, x2, x3
,x4,x5, x6, x7 ,x8,x9, \
x10, x11 ,x12,x13, x14, x15
,x16, x17,\
x18, x19 ,x20])

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可