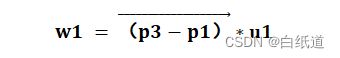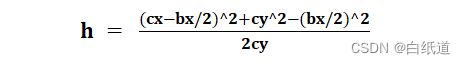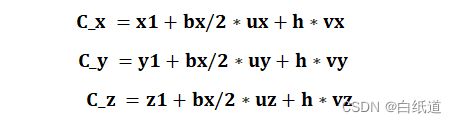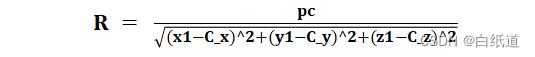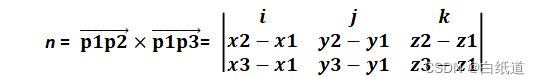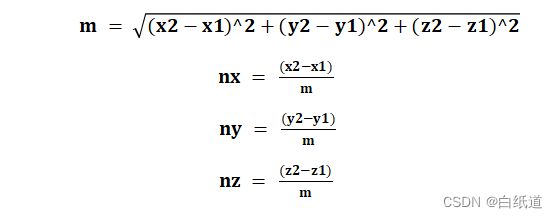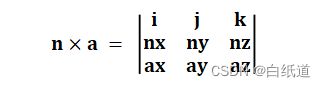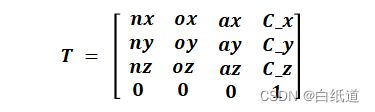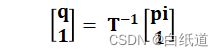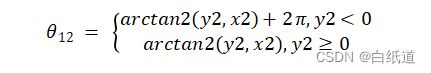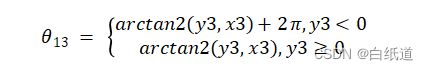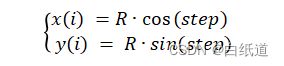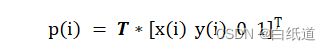机器人轨迹弧线规划
- 主要内容
- 弧线轨迹规划
- 主要思想：
一般情况下我们采用三点确定一个圆的方式（三角形外接圆）,在空间中如果我们需要直接确定弧线的中心坐标比较困难，所以我们需要将三维中的问题先转化到二维空间中解决，再将二维空间中的位置转换为三维空间中的位置数据。
-
- 公式推导：
第一步：
首先先确定空间中三点位置p1（x1,y1,z1）,p2（x2,y2,z2）,p3（x3,y3,z3）
以这空间三点为基准建立坐标系P1—UVW 确定U,V,W三轴的方向，首先确定U轴的方向：
（1）
确定了U轴的方向之后我们可以选择一个和U轴垂直的单位方向向量作为W轴,则我们定义：
（2）
我们获得了U轴和W轴的方向，我们需要求其单位向量（虽然说求到这一步我们已经基本可以确定轴的方向，但是后续我们需要单位向量来将三维空间中的数据真实的反应到二维中）：
（3）
（4）
根据式（3）、（4）我们可以得出V轴的方向以及其单位向量：
（5）
第二步：
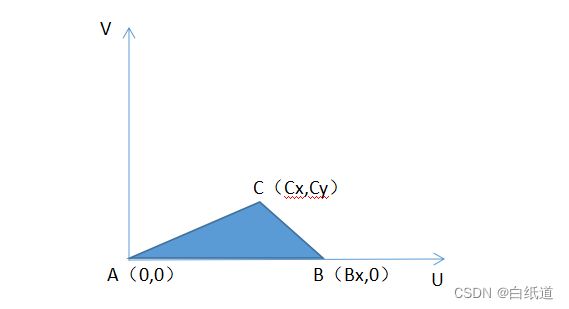
第一步中我们确定了以空间中三点建立的新坐标系P1—UVW，则在此步骤中我们将空间中三点转化到二维空间中来进行处理，我们确定以p1作为新平面坐标系（A—UV）的原点A(0,0)；p2，p3点在新平面坐标系上分别为B(bx,0)、C(cx,cy)，如下图：
Ps：为什么B点的坐标是(bx,0)呢？解释：主要是因为在第一步中p2点在U轴上，U轴转化到平面上后那么B点的坐标理所当然的就是(bx,0)了。
图1 空间中三点转化到二维平面上的位置信息
下面我们来具体推导B点和C点的位置数据（在B在U轴上的投影）：
（6）
求C位置数据方法同上（点C分别在UV轴上的投影）：
（7）
至此，我们获得ABC三点的所有位置数据。
第三步：
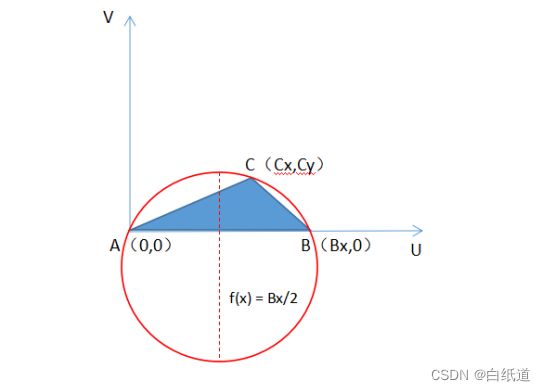
第一第二步完成了空间中点位置信息转化到平面上的公式推导和模型建立，第三步我们主要着手求其在平面中的圆心和半径信息,首先如图：
图2 二维平面上的位置信息
由图所示，我们可以确定圆心肯定在X = Bx/2上，那么我们设圆心为,圆上任意一点为根据圆的标准公式我们可以建立该方程：
（8）
根据（8）式我们可以求得位置参数h：
（9）
根据上述公式推导，我们可以确定空间中圆弧的中心，我们设其为Pc(C_x,C_y,C_z),
p1(x1,y1,z1),p2p3依次类推,U = [ux,uy,uz],可以求得：
（10）
我们通过（10）可以求得空间中圆弧的中心点
我们也可以求得其在三维空间中的半径R：
（11）
第四步：
在一二三步中我们求得了圆弧在空间中的中心和其半径，在第四步中我们主要讨论在空间中的弧线插补公式推导。
最主要的核心思想是将空间中三点反映到我们建立的新坐标系UVW上进行一个平面的弧线处理（空间圆弧本质上是三个空间点形成平面(平面M)上的圆弧,我们只要求出坐标系在坐标系O − X Y Z下的变换矩阵T ,就可经过坐标变换将三维空间(O − X Y Z)的圆弧变换到二维平面(P0−UVW)的圆弧）
为此，我们需要求出变换矩阵T，将空间中任意一点可以通过该变换矩阵反映到我们的新坐标系上，然后进行插补运算。
Ps：如何建立该变换矩阵T？回答：建立该变换矩阵的重要思想是将空间坐标系的各个轴（XYZ）反映到新建立的坐标系上各个轴（UVW），那么据此我们就需要用各个轴的方向余弦构建该矩阵T。
首先，先确定该平面的法向量，即W轴，并且求其在XYZ上的方向余弦（方向余弦：与三个轴之间的角度的余弦）
在该平面中确定两个向量，然后求其×积，我们就可以求得该平面的法向量，设平面法向量为n，则有：
（12）
记n = {A,B,C}，则W轴各方向余弦为：
（13）
U轴各方向余弦为：
（14）
V轴各方向余弦为：
（15）
可以求得[ox,oy,oz]
至此，我们可以求得变换矩阵T
（16）
近而我们可以求出p1,p2,p3在新坐标系下的值(i = 1,2,3)：
（17）
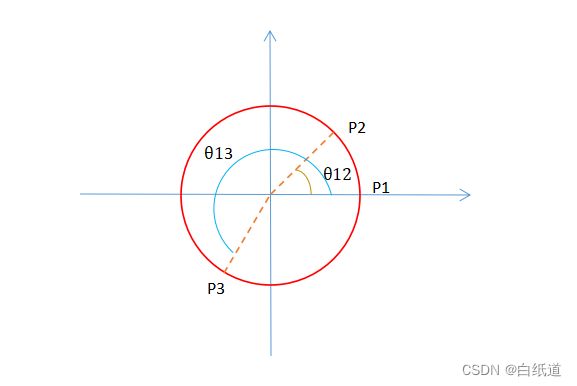
至此，我们求得空间中三点在新坐标系上的位置信息,并且我们可以确定圆弧的总插补角，如下图
图3 空间中三点决定的圆弧
如图，我们可以求得其圆弧的总插补角：
（18）
（19）
我们以总圆弧的弧度作为插补最大弧度值，从0到插补最大值/插补次数到插补最大弧度值（此值记为step），并且我们根据上述公式和图式可以推导每个插补的点位信息：
（20）
则插补点在基座标系内的坐标为：
（21）
至此，我们建立弧线轨迹规划模型和插补模型。