机器学习之随机森林、GBDT、Xgboost
随机森林 、GBDT 与 Xgboost 详细推导
- 一. 决策树——有监督学习
- 二. 随机森林
- 三. GBDT
- 四. Xgboost
- 四. 参考文献及链接
写在前面的话:这部分内容主要是基本概念与实现方法,便于回顾使用。很多数学公式我看着也头大,得慢慢吸收,多看几遍就差不多了。
损失函数是最小平方误差、绝对值误差等,则为回归问题;而误差函数换成多类别Logistic似然函数,则成为分类问题。
一. 决策树——有监督学习
决策树: 从根节点到叶子节点 (节点),既可以做分类,也可以做回归,所有的数据最终都会落在叶子节点,决策树学习采用的是自顶向下的递归方法,以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零,此时每个叶节点中的实例属于同一类
树的组成: 根节点,非叶子节点与分支,叶子节点
衡量标准:信息熵: 表示信息的复杂度,即不确定性。下式中 I I I为信息量,H(D)为标签的信息熵 H ( D ) = − ∑ i = 1 M P i ⋅ l o g 2 ( P i ) I = − l o g 2 P H(D) =-\sum_{i=1}^{M}P_i \cdot log_2(P_i) \quad I = - log_2P H(D)=−i=1∑MPi⋅log2(Pi)I=−log2P
-
信息增益(ID3算法): 信息增益越大,则权重越大。一般训练出来深度浅但又庞大。H(A)为特征的信息熵 g ( D , A ) = H ( D ) – H ( D ∣ A ) g(D,A)=H(D) – H(D|A) g(D,A)=H(D)–H(D∣A)
-
增益率(C4.5算法): g r ( D , A ) = g ( D , A ) / H ( A ) gr(D,A) = g(D,A) / H(A) gr(D,A)=g(D,A)/H(A)
-
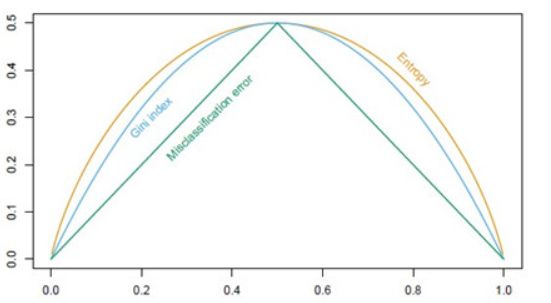
Gini系数(CART算法): G i n i ( p ) = ∑ i = 1 M p i ( 1 − p i ) = 1 − ∑ i = 1 M p i 2 Gini(p) = \sum^{M}_{i=1}p_i(1-p_i)=1-\sum^{M}_{i=1}p_i^2 Gini(p)=i=1∑Mpi(1−pi)=1−i=1∑Mpi2
Gini系数的图像、熵、分类误差率三者
之间的关系:
剪枝处理: 决策树对未知的测试数据未必有好的分类能力,泛化能力弱,节点划分将不断重复,造成分支过多,即可能发生过拟合现象,因此可主动去掉一些分支降低过拟合的风险。可分为 预剪枝 (边建立决策树边剪枝) 和 后剪枝 (建完决策树后再剪枝)。
- 计算所有内部节点的剪枝系数;
- 查找最小剪枝系数的结点,剪枝得决策树Tk ;
- 重复以上步骤,直到决策树Tk只有1个结点;
- 得到决策树序列T0T1T2…TK ;
- 使用验证样本集选择最优子树
from sklearn.tree import DecisionTreeClassifier
# Make a decision tree and train
tree = DecisionTreeClassifier(random_state=RSEED)
tree.fit(X, y)
DecisionTreeClassifier(class_weight=None, criterion=‘gini’, max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=50,
splitter=‘best’)
二. 随机森林
集成模型: 即多个分类器组成一个强分类器。如果每一步的弱预测模型生成都是依据损失函数的梯度方向,则称之为梯度提升(Gradient boosting)
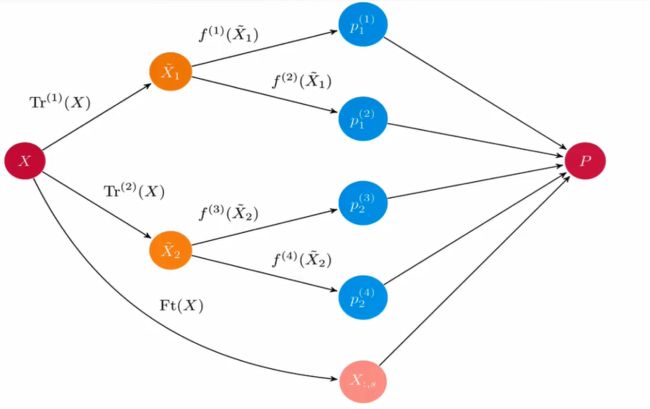
Bagging: 是bootstrap aggregation,一种有放回的抽样方法,并行训练多个分类器。训练m个分类器再投入数据进行投票、平均或学习选取
如上图,用不同的方法预处理,再用不同的算法进行训练,最终得出一个最优模型
Boosting: 弱分类器开始加强,通过加权进行训练 F m ( x ) = F m − 1 ( x ) + a r g m i n h ∑ i = 1 n L ( y i , F m − 1 ( x i ) + h ( x i ) ) F_m(x) = F_{m-1}(x)+argmin_h \sum_{i=1}^{n}L(y_i,F_{m-1}(x_i)+h(x_i)) Fm(x)=Fm−1(x)+argminhi=1∑nL(yi,Fm−1(xi)+h(xi))
AdaBoost:,Adaptive Boosting (自适应增
强) ,是Boosting的一种。不需要预先知道弱学习算法学习正确率的下限即弱分类器的误差,并且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度,这样可以深入挖掘弱分类器算法的能力。 AdaBoost算法中不同的训练集是通过调整每个样本对应的权重来实现的,对于噪声数据和异常数据很敏感。
- 设训练数据集T={(x1,y1), (x2,y2)…(xN,yN)}
- 初始化训练数据的权值分布 D 1 = ( w 11 , w 12 ⋯ w 1 i ⋯ w 1 N ) , w 1 i = 1 N , i = 1 , 2 , ⋯ , N D_1 = (w_{11},w_{12}\cdots w_{1i}\cdots w_{1N}), \quad w_{1i}=\frac{1}{N},\quad i=1,2,\cdots,N D1=(w11,w12⋯w1i⋯w1N),w1i=N1,i=1,2,⋯,N
- 使用具有权值分布Dm的训练数据集学习,得到基本分类器 G m ( x ) : χ → { − 1 , + 1 } \quad G_m(x): χ\rightarrow \{-1,+1\} Gm(x):χ→{−1,+1}
- 计算Gm(x)在训练数据集上的分类误差率 e m = P ( G m ( x i ) ≠ y i ) = ∑ i = 1 N w m i I ( G m ( x i ) ≠ y i ) e_m = P(G_m(x_i)≠y_i) = \sum^{N}_{i=1}w_{mi}I(G_m(x_i)≠y_i) em=P(Gm(xi)̸=yi)=i=1∑NwmiI(Gm(xi)̸=yi)
- 计算Gm(x)的系数 α m = 1 2 l o g 1 − e m e m \quad α_m = \frac{1}{2}log\frac{1-e_m}{e_m} αm=21logem1−em
- 更新训练数据集的权值分布, 它的目的仅仅是使 D m + 1 D_{m+1} Dm+1 成为一个概率分布 D m + 1 = ( w m + 1 , 1 , w m + 1 , 2 ⋯ w m + 1 , i ⋯ w m + 1 , N ) , w m + 1 , i = w m i Z m e x p ( − α m y i G m ( x i ) ) , i = 1 , 2 , ⋯ , N D_{m+1} = (w_{m+1,1},w_{m+1,2}\cdots w_{m+1,i}\cdots w_{m+1,N}), \quad w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-α_my_iG_m(x_i)),\quad i=1,2,\cdots,N Dm+1=(wm+1,1,wm+1,2⋯wm+1,i⋯wm+1,N),wm+1,i=Zmwmiexp(−αmyiGm(xi)),i=1,2,⋯,N
- 构建基本分类器的线性组合 f ( x ) = ∑ m = 1 M α m G m ( x ) f(x) = \sum_{m=1}^{M}α_mG_m(x) f(x)=m=1∑MαmGm(x)
- 得到最终分类器 G ( x ) = s i g n ( f ( x ) ) = s i g n ( ∑ m = 1 M α m G m ( x ) ) G(x)=sign(f(x))=sign(\sum_{m=1}^{M}α_mG_m(x)) G(x)=sign(f(x))=sign(m=1∑MαmGm(x))
Stacking: 堆叠模型,聚合多个分类或回归模型。下一阶段用不同的分类器前一阶段的结果训练。会赋给不同分类器权重。
随机森林: 建立m棵CART决策树,这m个CART形成随机森林,通过投票、平均或学习决定数据属于哪一类。(ensemble model made of hundreds or thousands of decision trees using bootstrapping, random subsets of features, and average voting to make predictions.)
随机森林/Bagging和决策树的关系: 决策树为基本分类器(弱分类器),基本分类器组成的总分类器叫做随机森林。
随机森林优势: 特征多,能处理高维度的数据,速度较快便于可视化分析
from sklearn.ensemble import RandomForestClassifier
# Create the model with 100 trees
model = RandomForestClassifier(n_estimators=100,
random_state=RSEED,
max_features = 'sqrt',
n_jobs=-1, verbose = 1)
# Fit on training data
model.fit(train, train_labels)
三. GBDT
GBDT 是 GB 和 DT 的结合,这里的决策树是回归树,基于 CART 树。
- 提升算法
给定输入向量x和输出变量y组成的若干训练样本(x1,y1),(x2,y2),…,(xn,yn),目标是找到近似函数F(x),使得损失函数L(y,F(x))的损失值最小,则L(y,F(x))的典型定义为: L ( y , F ( x ⃗ ) ) = 1 2 ( y − F ( x ⃗ ) ) 2 L(y,F( \vec {x}))=\frac{1}{2}(y-F( \vec {x}))^2 L(y,F(x))=21(y−F(x))2
假定最优函数为: F ∗ ( x ⃗ ) = a r g m i n F E ( x , y ) [ L ( y , F ( x ⃗ ) ) ] F^*(\vec{x}) = arg min_FE_{(x,y)}[L(y,F(\vec{x}))] F∗(x)=argminFE(x,y)[L(y,F(x))]
假定F(x)是一族基函数 f i ( x ) f_i(x) fi(x)的加权和 F ( x ⃗ ) = ∑ i = 1 M γ i f i ( x ) + c o n s t F(\vec{x}) = \sum_{i=1}^{M}γ_if_i(x)+const F(x)=i=1∑Mγifi(x)+const
梯度提升方法寻找最优解F(x),使得损失函数在训练集上的期望最小。首先,给定 常函数F0(x): F 0 ( x ⃗ ) = a r g m i n γ ∑ i = 1 n L ( y i , γ ) F_0(\vec{x})=argmin_γ \sum^{n}_{i=1}L(y_i,γ) F0(x)=argminγi=1∑nL(yi,γ)
以贪心的思路扩展得到Fm(x): F m ( x ⃗ ) = F m − 1 ( x ⃗ ) + a r g m i n f ∈ H ∑ i = 1 n [ L ( y i , F m − 1 ( x i ⃗ ) + f ( x i ⃗ ) ) ] F_m(\vec{x}) = F_{m-1}(\vec{x})+arg min_{f∈H}\sum^{n}_{i=1}[L(y_i,F_{m-1}(\vec{x_i})+f(\vec{x_i}))] Fm(x)=Fm−1(x)+argminf∈Hi=1∑n[L(yi,Fm−1(xi)+f(xi))]
梯度近似: 贪心法在每次选择最优基函数f时仍然困难,使用梯度下降的方法近似计算,样本带入基函数f得到f(x1),f(x2),…,f(xn),从而L退化为向量L(y1,f(x1)),L(y2,f(x2)),…,L(yn,f(xn)) F m ( x ⃗ ) = F m − 1 ( x ⃗ ) − γ m ∑ i = 1 n ∇ f L ( y i , F m − 1 ( x i ⃗ ) ) F_m(\vec{x}) =F_{m-1}(\vec{x})-γ_m\sum^{n}_{i=1}\nabla_fL(y_i,F_{m-1}(\vec{x_i})) Fm(x)=Fm−1(x)−γmi=1∑n∇fL(yi,Fm−1(xi))
上式中的权值γ为梯度下降的步长,使用线性搜索求最优步长: γ m = a r g m i n γ ∑ i = 1 n L ( y i , F m − 1 ( x i ⃗ ) − γ ⋅ ∇ f L ( y i , F m − 1 ( x i ⃗ ) ) ) γ_m=argmin_γ \sum^{n}_{i=1}L(y_i,F_{m-1}(\vec{x_i})-γ \cdot \nabla_fL(y_i,F_{m-1}(\vec{x_i}))) γm=argminγi=1∑nL(yi,Fm−1(xi)−γ⋅∇fL(yi,Fm−1(xi)))
对于m=1到 M,伪残差 (基于Loss Function函数空间的负梯度的学习也称为“伪残差”) r i m = [ ∂ L ( y i , F ( x i ⃗ ) ) ∂ F ( x i ⃗ ) ] F ( x ⃗ ) = F m − 1 ( x ⃗ ) i = 1 , 2 , ⋯ , n r_{im}=[\frac{\partial L(y_i,F(\vec{x_i}))}{\partial F(\vec{x_i})}]_{F(\vec{x})=F_{m-1}(\vec{x})} \quad i=1,2,\cdots,n rim=[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x)i=1,2,⋯,n
使用数据计算拟合残差的基函数 f m ( x ) f_m (x) fm(x),再计算步长 (一维优化) γ m = a r g m i n γ ∑ i = 1 n L ( y i , F m − 1 ( x i ⃗ ) − γ ⋅ F m ( x i ⃗ ) ) γ_m=argmin_γ \sum^{n}_{i=1}L(y_i,F_{m-1}(\vec{x_i})-γ \cdot F_{m}(\vec{x_i})) γm=argminγi=1∑nL(yi,Fm−1(xi)−γ⋅Fm(xi))
更新模型 F m ( x ⃗ ) = F m − 1 ( x ⃗ ) − γ m f m ( x i ⃗ ) F_m(\vec{x}) = F_{m-1}(\vec{x})-γ_mf_m(\vec{x_i}) Fm(x)=Fm−1(x)−γmfm(xi)
- 梯度提升决策树GBDT
在第m步的梯度提升是根据伪残差数据计算决策树 t m ( x ⃗ ) t_m(\vec{x}) tm(x)。令树 t m ( x ⃗ ) t_m(\vec{x}) tm(x) 的叶节点数目为J,即树 t m ( x ⃗ ) t_m(\vec{x}) tm(x) 将输入空间划分为J个不相交区域 R 1 m , R 2 m , . . . , R j m R_{1m},R_{2m},...,R_{jm} R1m,R2m,...,Rjm,并且决策树tm(x)可以在每个区域中给出某个类型的确定性预测。使用指示记号 I ( x ) I(x) I(x),对于输入 x x x, t m ( x ⃗ ) t_m(\vec{x}) tm(x) 为:
t m ( x ⃗ ) = ∑ j = 1 J b j m I ( x ⃗ ∈ R j m ) t_m(\vec{x})=\sum^{J}_{j=1}b_{jm}I(\vec{x}∈R_{jm}) tm(x)=j=1∑JbjmI(x∈Rjm)
b j m b_{jm} bjm 是样本 x x x 在区域 R j m R_{jm} Rjm 的预测值,使用线性搜索计算学习率,最小化损失函数:
F m ( x ⃗ ) = F m − 1 ( x ⃗ ) − γ m t m ( x i ⃗ ) F_m(\vec{x}) = F_{m-1}(\vec{x})-γ_mt_m(\vec{x_i}) Fm(x)=Fm−1(x)−γmtm(xi)
γ m = a r g m i n γ ∑ i = 1 n L ( y i , F m − 1 ( x i ⃗ ) − γ ⋅ t m ( x i ⃗ ) ) γ_m=argmin_γ \sum^{n}_{i=1}L(y_i,F_{m-1}(\vec{x_i})-γ \cdot t_{m}(\vec{x_i})) γm=argminγi=1∑nL(yi,Fm−1(xi)−γ⋅tm(xi))
对树的每个区域分别计算步长,从而系数 b j m b_{jm} bjm 被合并到步长中,从而: F m ( x ⃗ ) = F m − 1 ( x ⃗ ) + ∑ j = 1 J γ j m I ( x ⃗ ∈ R j m ) F_m(\vec{x}) = F_{m-1}(\vec{x})+\sum^{J}_{j=1}γ_{jm}I(\vec{x}∈R_{jm}) Fm(x)=Fm−1(x)+j=1∑JγjmI(x∈Rjm) γ k = j m = a r g m i n γ ∑ x i ∈ R j m ⃗ L ( y i , F m − 1 ( x i ⃗ ) + γ ⋅ t m ( x i ⃗ ) ) γ_{k=jm}=argmin_γ \sum_{\vec{x_i∈R_{jm}}}L(y_i,F_{m-1}(\vec{x_i})+γ \cdot t_{m}(\vec{x_i})) γk=jm=argminγxi∈Rjm∑L(yi,Fm−1(xi)+γ⋅tm(xi))
参数 J 控制数的结构, M 为迭代次数,值选取过大可能造成过拟合
四. Xgboost
Xgboost 是一种 提升算法 ,其基本思想是把多个分类准确率较低的树模型组合起来,成为一个准确率很高的模型。特点在于迭代,每迭代一次就生成一颗新的树。其中采用梯度下降的思想,以之前生成的所有决策树为基础,向着最小化给定目标函数的方向进一步。能够自动利用 CPU 的多线程进行并行。
目标函数:
- Square loss: l ( y i , y i ^ ) = ( y i − y i ^ ) 2 \qquad l(y_i,\hat{y_i})=(y_i - \hat{y_i})^2 l(yi,yi^)=(yi−yi^)2
- Logistic loss: l ( y i , y i ^ ) = y i l n ( 1 + e − y i ^ ) + ( 1 − y i ) l n ( 1 + e y i ^ ) \qquad l(y_i,\hat{y_i})=y_i ln( 1+ e^{-\hat {y_i}})+(1-y_i) ln( 1+ e^{\hat {y_i}}) l(yi,yi^)=yiln(1+e−yi^)+(1−yi)ln(1+eyi^)
第一个函数就是距离,第二个函数就是很明显的二分类,
最优解: F ∗ ( x ⃗ ) = a r g m i n E ( x , y ) [ L ( y , F ( x ⃗ ) ) ] F^*(\vec{x}) = arg minE_{(x,y)}[L(y,F(\vec{x}))] F∗(x)=argminE(x,y)[L(y,F(x))]
算法表示: y i ^ = ∑ k = 1 K f k ( x i ) , f k ∈ F \hat {y_i} = \sum^{K}_{k=1}f_k(x_i),f_k∈ F yi^=k=1∑Kfk(xi),fk∈F
基础模型为决策树模型,集成方法是累加的,也就是说是一堆 CART 树构成的:
y i ^ ( 0 ) = 0 \hat{y_i}^{(0)} = 0 yi^(0)=0
y i ^ ( 1 ) = f 1 ( x i ) = y i ^ ( 0 ) + f 1 ( x i ) \hat{y_i}^{(1)} = f_1(x_i) = \hat{y_i}^{(0)} +f_1(x_i) yi^(1)=f1(xi)=yi^(0)+f1(xi)
y i ^ ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y i ^ ( 1 ) + f 2 ( x i ) \hat{y_i}^{(2)} = f_1(x_i) +f_2(x_i)= \hat{y_i}^{(1)} +f_2(x_i) yi^(2)=f1(xi)+f2(xi)=yi^(1)+f2(xi)
⋯ \cdots ⋯
y i ^ ( t ) = ∑ k = 1 t f k ( x i ) + f 2 ( x i ) = y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}^{(t)} = \sum_{k=1}^{t}f_k(x_i) +f_2(x_i)= \hat{y_i}^{(t-1)} +f_t(x_i) yi^(t)=k=1∑tfk(xi)+f2(xi)=yi^(t−1)+ft(xi)
优化目标函数: 就是原 loss 函数加上了正则项,即误差分析,目的就是找到 f t f_t ft 来优化目标。既要做误差,又不能使我们建立的树模型太过庞大,要限制叶子的个数,因此有下面的式子
O b j ( t ) = ∑ i = 1 n l ( y i , y i ^ ( t ) ) + ∑ i = 1 t Ω ( f i ) = ∑ i = 1 n l ( y i , y i ^ ( t ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t Obj^{(t)} = \sum^{n}_{i=1}l(y_i,\hat{y_i}^{(t)})+\sum^{t}_{i=1}Ω(f_i)= \sum^{n}_{i=1}l(y_i,\hat{y_i}^{(t)} + f_t(x_i)) +Ω(f_t)+constant Obj(t)=i=1∑nl(yi,yi^(t))+i=1∑tΩ(fi)=i=1∑nl(yi,yi^(t)+ft(xi))+Ω(ft)+constant
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 Ω(f_t)=γT+ \frac{1}{2}λ \sum^{T}_{j=1}w_j^2 Ω(ft)=γT+21λj=1∑Twj2
(1)在 Ω ( f t ) Ω(f_t) Ω(ft) 中 γ T γT γT 表示叶子的个数,后半部分是L2正则 (所有参数的平方和),让树模型更精简,就是这个惩罚项无限接近于 0,即对叶子和权重做了正则化。 (2) γ γ γ 越大,表示获得结构越简单的树,因为此时对较多叶子节点的树的惩罚越大。 λ λ λ 一样。这两个参数都是自己设定(3)那么问题来了,为什么要加上 1 2 \frac{1}{2} 21 ? 先往后看
利用残差法我们的得到新的目标函数 ( y i ^ ( t − 1 ) − y i \hat{y_i}^{(t-1)} -y_i yi^(t−1)−yi 为残差):
O b j ( t ) = ∑ i = 1 n ( y i − ( y i ^ ( t − 1 ) + f t ( x i ) ) ) 2 + Ω ( f t ) = ∑ i = 1 n [ 2 ( y i ^ ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 ] + Ω ( f t ) + c o n s t a n t Obj^{(t)} = \sum^{n}_{i=1}(y_i-(\hat{y_i}^{(t-1)}+f_t(x_i)))^2+Ω(f_t)= \sum^{n}_{i=1}[2(\hat{y_i}^{(t-1)} -y_i)f_t(x_i)+f_t(x_i)^2] +Ω(f_t)+constant Obj(t)=i=1∑n(yi−(yi^(t−1)+ft(xi)))2+Ω(ft)=i=1∑n[2(yi^(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)+constant
上式中 f t ( x i ) f_t(x_i) ft(xi) 是叶子节点的值,叶子节点的值可以作为模型的参数。接下来我们定义 ( g i g_i gi 为一阶导, h i h_i hi 为二阶导):
g i = ∂ y t − 1 ^ l ( y i , y i ^ ( t − 1 ) ) , h i = ∂ y t − 1 ^ 2 l ( y i , y i ^ ( t − 1 ) ) g_i = \partial_{\hat{y^{t-1}}}l(y_i,\hat{y_i}^{(t-1)}), \quad h_i = \partial_{\hat{y^{t-1}}}^2l(y_i,\hat{y_i}^{(t-1)}) gi=∂yt−1^l(yi,yi^(t−1)),hi=∂yt−1^2l(yi,yi^(t−1))
可以转换目标函数近似为:
O b j ( t ) ≈ ∑ i = 1 n [ l ( y i , y i ^ ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) + c o n s t a n t Obj^{(t)}≈\sum_{i=1}^{n}[ l(y_i,\hat{y_i}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)] +Ω(f_t)+constant Obj(t)≈i=1∑n[l(yi,yi^(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)+constant
= ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) =\sum_{i=1}^{n}[ g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+Ω(f_t) =i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)
= ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + γ T + 1 2 λ ∑ j = 1 T w j 2 =\sum_{i=1}^{n}[ g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+γT+ \frac{1}{2}λ \sum^{T}_{j=1}w_j^2 =i=1∑n[gift(xi)+21hift2(xi)]+γT+21λj=1∑Twj2
= ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T =\sum^{T}_{j=1}[(\sum_{i∈I_j}g_i)w_j+\frac{1}{2}(\sum_{i∈I_j}h_i+\lambda)w_j^2]+γT =j=1∑T[(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2]+γT
(1)先解释下为什么用 g i g_i gi 与 h i h_i hi ,是因为这里运用了二阶泰勒展开式。(2)解释上面的问题,这里也有个 1 2 \frac{1}{2} 21 ,首先知道二阶泰勒展开的二次项有个 1 2 \frac{1}{2} 21,为了合并到一起,所以之前加了个 1 2 \frac{1}{2} 21,(3) x i x_i xi 是样本,接下来就要求每个 x i x_i xi,那么就需要对每一个样本进行遍历,这样计算量就会很大,因此要转换方向,由于每一个样本最终都会落到其中一个叶子节点上,那么就可以转换为遍历叶子节点 ( T T T 是叶子节点个数, n n n 是样本个数)。(4) ( ∑ i ∈ I j g i ) w j (\sum_{i∈I_j}g_i)w_j (∑i∈Ijgi)wj 的意思就是最终某一个叶子节点的样本个数和乘以其权重,也表明遍历的是叶子节点
constant 是前 t-1 棵树的正则化项, l ( y i , y i ^ ( t − 1 ) ) l(y_i,\hat{y_i}^{(t-1)}) l(yi,yi^(t−1)) 也是常数项,为使目标函数最小化,则直接去掉常数项,便成了最后的式子 (最后一个等号),式中 γ T γT γT 为整个树的正则项。树的一次式,二次式,其实都是某个叶子节点的值的一次式,二次式。式中 w j w_j wj 其实就是树最终的结果 (叶子节点的值),前面说过了,其值可以作为模型的变量。
我们对目标函数再作简化:令
G j = ∑ i ∈ I j g i , H j = ∑ i ∈ I j h i G_j = \sum_{i∈I_j}g_i \qquad, \qquad H_j =\sum_{i∈I_j}h_i Gj=i∈Ij∑gi,Hj=i∈Ij∑hi
O b j ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T Obj^{(t)} =\sum^{T}_{j=1}[(\sum_{i∈I_j}g_i)w_j+\frac{1}{2}(\sum_{i∈I_j}h_i+\lambda)w_j^2]+γT=\sum^{T}_{j=1}[G_jw_j + \frac{1}{2}(H_j+\lambda)w_j^2]+γT Obj(t)=j=1∑T[(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2]+γT=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT
这样做的原因是每一个叶子节点内都是一样的,因此直接变为内部样本的和。此时: G j G_j Gj 对应模型的一阶导, H j H_j Hj 对应模型的二阶导。接下来就是要求最小值——求偏导 (对 w j w_j wj 求导)
∂ J ( f t ) ∂ w j = G j + ( H j + λ ) w j = 0 \frac {\partial J(f_t)}{\partial w_j} = G_j+(H_j+\lambda)w_j = 0 ∂wj∂J(ft)=Gj+(Hj+λ)wj=0
得到 w j = − G j H j + λ w_j = -\frac{G_j}{H_j+\lambda} wj=−Hj+λGj
带回原目标函数得到:
O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\frac{1}{2}\sum_{j=1}^{T} \frac{G_j^2}{H_j+\lambda}+γT Obj=−21j=1∑THj+λGj2+γT
G j 2 H j + λ \frac{G_j^2}{H_j+\lambda} Hj+λGj2 用来衡量模型的效果,越小说明树结构越好。xgboost的优势就在于速度快 (因为在计算每个叶节点是并行计算的,它们之间毫无关系),准确度高
放一段xgboost调用的代码,代码来自于 Santhosh Sharma Ananthramu
#Evaluation of various combinations of XGB
#Import the library
from xgboost import XGBRegressor
#Add the n_estimators value to the below list if you want to run the algo
n_list = numpy.array([])
for n_estimators in n_list:
#Set the base model
model = XGBRegressor(n_estimators=n_estimators,seed=seed)
algo = "XGB"
#Accuracy of the model using all features
for name,i_cols_list in X_all:
model.fit(X_train[:,i_cols_list],Y_train)
result = mean_absolute_error(numpy.expm1(Y_val), numpy.expm1(model.predict(X_val[:,i_cols_list])))
mae.append(result)
print(name + " %s" % result)
comb.append(algo + " %s" % n_estimators )
if (len(n_list)==0):
mae.append(1169)
comb.append("XGB" + " %s" % 1000 )
四. 参考文献及链接
[1] 《机器学习》 周志华著
[2] 《机器学习中文版》 Tom M. Mitchell著
[3] 《Python 机器学习及实践》 范淼、李超著
[4] xgboost的原理没你想像的那么难
[5] https://xgboost.readthedocs.io/en/latest/tutorials/dart.html 这个手册是真的详细!!!
[6] 一步一步理解GB、GBDT、xgboost