ResNet 残差、退化等细节解读
说实话ResNet的网络结构参数真没有什么可以解读的,在本博客中我们主要了解(1)传统深度学习网络的退化问题(2)ResNet到底解决了什么问题?(3)简单了解下ResNet和残差结构(4)残差结构如何解决退化问题(5)残差结构还有什么其他作用?
2016年CVPR Best Paper https://arxiv.org/abs/1512.03385 何凯明大神的作品。。有空多看看。
1. 深度学习网络的退化问题
自AlexNet以来,以CNN为基石的网络模型越来越深(层数越来越多)。AlexNet有5个卷积层,VGG有19层,GoogleNet( 也称Inception_v1)有22层。之所以这么一直在增加网络深度,是有这么一个理论:根据卷积的计算方式,我们认为深度卷积网络逐层整合了不同层级的特征,伴随着模型前向推演,模型获得了更加抽象、更多层级、更加丰富的图像特征,进而获得了更好的模型性能。因此我们会倾向于使用更深层次的网络结构!!!!
补充:低层级特征拥有更多的细节信息;高层级特征更加抽象,能够更好的表达图像局部或者整体的意义。
但是经过试验证明,很深的网络一般会有两个问题:
(1)在很深的网络层中,由于参数初始化一般更接近0,这样在训练过程中通过反向传播更新浅层网络的参数时,很容易随着网络的深入而导致梯度消失,浅层的参数无法更新。
(2)当网络达到一定深度后,模型性能会暂时陷入一个瓶颈很难增加,当网络继续加深后,模型在测试集上的性能反而会下降!这其实就是深度学习退化(degradation)!
来看一下ResNet论文中的实验结果图。
下图简单来讲,就是在CIFAR-10这个数据集上,分别使用20层和56层的神经网络去训练。左图是训练误差,右图是测试误差。
我们看图可以发现无论是在训练集还是在测试集上,56层的神经网络性能都不如20的神经网络。
注意:造成这种现象的原因有(1)过拟合(2)梯度消失/梯度爆炸(3)网络退化。
(1)不可能是过拟合
过拟合是过多的拟合了训练集,因此在训练集上效果好(偏差低),而在测试集上效果差(方差高)。但是我们发现无论是训练集误差还是测试集误差其实都在下降,只是幅度不一样。这说明了更深的网络性能不好是因为网络没有被训练好,其原因是后面的多层非线性网络无法通过训练去逼近恒等映射网络。
解释一下上面红字的意思:通常认为在同一个训练集上,深层网络的性能无论如何都不应该比浅层网络差。假设A是一个56层的网络,B是一个20层的网络,若想让A和B拥有同样的性能,只需要将A中的20层替换为B,然后将A中剩下的36层全部优化为恒等映射(即输入=输出)。但是实验证明,后面36层的非线性网络很难学习逼近恒等映射(看图即可得到)。
(2)不是梯度消失/梯度爆炸
作者在论文中说到,理论上的梯度消失和梯度爆炸都应该被批量归一化 Batch normalization(BN)解决了。BN通过规整数据的分布解决梯度消失/爆炸的问题。
2. 深层CNN为何发生退化? and ResNet到底解决了什么问题?
比较好的解释来自于这篇2017年的论文 The Shattered Gradients Problem: If resnets are the answer, then what is the question?
论文大意是当神经网络越来越深,在反向传播时候,反传回来的梯度之间的相关性会越来越差,最后接近白噪声。因为我们知道图像是具备局部相关性的,那其实可以认为梯度也应该具备类似的相关性,这样更新的梯度才有意义,如果梯度接近白噪声,那梯度更新可能根本就是在做随机扰动。即使BN过后梯度的模稳定在了正常范围内,但梯度的相关性实际上是随着层数增加持续衰减的。而经过证明,ResNet可以有效减少这种相关性的衰减。
理论上这种相关性的衰减越少,说明反向传播回来的信息(可以说是相关性也可以说是梯度)的丢失/损失越少,梯度的更新就更具有实际意义(根据特定目标的有规律更新而不是随机扰动),在本节的论文中作者以相关性这个指标为核心,分析了一系列的网络结构和激活函数的影响,得出结论:对于一共L层的网络,没有残差结构的普通网络相关性的衰减在![]() (可以看到是指数级别的衰减),而ResNet的衰减率只有
(可以看到是指数级别的衰减),而ResNet的衰减率只有![]() 。注:这是论文作者给出的结论,我其实没有证明,后续有时间再开一篇博客单独说这个衰减率的计算!!!
。注:这是论文作者给出的结论,我其实没有证明,后续有时间再开一篇博客单独说这个衰减率的计算!!!
因此,个人认为 只要网络由深度,无论是前向传播还是反向传播一定会出现信息的丢失或者说衰减,只是大小的问题,而ResNet 残差结构的存在使得这种梯度相关性的衰减得到了减少,延缓网络退化问题的出现(注:这里说的是“延缓”,个人认为无论如何缓解这种相关性的衰减,它必然存在,因此当网络到了一定深度之后,深层网络的梯度对于浅层网络权重更新的影响依然会变得非常小,这就又出现了退化,这种情况不可避免)。
3. 简单了解下ResNet和残差结构
如果你是从本文1,2节按照顺序看下来的,就会知道 想要神经网络学习恒等映射是很困难的(原因有待考究,不好表述,可能每个人对于这个问题都有自己的见解),这也是为什么56层网络的性能反而不如20层网络的原因。那么现在我们不去学习恒等映射,换个思路,去学习输入和输出的差值,如果学习出的差值趋近于0,其实也能得到恒等映射,这样间接实现了恒等映射。
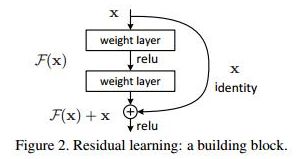
下图就是ResNet 残差结构的一个抽象图:我们假定输入x,输出y,需要学习的残差函数f(x),那么现在的前向传播就变成了
y = f(x) + x 。
下面这张图,就是ResNet论文中残差结构的实际结构(原文提出了18,34,50,101,152 共计5种不同深度的ResNet,18和34层的ResNet的残差结构如下图左所示,更深层的3种ResNet残差结构对应右图)
ResNet论文给出的所有模型的结构说明:如果你还想学习关于网络结构的具体细节,可以直接去搜下相关博客,这方面还是挺多的,这里就不多描述了。
4. 残差结构如何解决退化问题
同样假定输入x,输出y,需要学习的残差函数f(x),引入ResNet后的前向传播就变成了y = f(x) + x
在引入ResNet之前,如果我们想要使得深度网络不出现退化问题,核心是要让较深的网络学习到的参数满足y=x,但是实验发现,想要让神经网络学习到权重/参数满足y = x 这一类恒等映射时比较困难。
因此,ResNet想到避免去学习权重满足 恒等映射,转而将前向传播修改成 y = f(x) + x 。我们发现,想让当前神经网络层学习到恒等映射,只需要让残差函数f(x) = 0,而学习f(x) = 0 比直接学习 y = x 要简单多。为啥那?原因的话这篇博客给了一个解释,博客地址:学习f(x) = 0 比 y = x简单的多
简单的讲就是,因为网络权重的初始化一般偏向于0,前向传播的计算往往是类似于这样的 y = g(wx + b),当权重w很小的时候 (wx+b)理论上也会很小,进而网络层学习残差 f(x) = 0的更新参数能够更快收敛。具体可以看看上面那篇博客,里面有图。
5. 残差结构还有什么其他作用?
ResNet的残差结构本质上是解决网络退化问题,同时它还可以解决梯度消失。
梯度消失:引入了残差结构后的前向传播抽象的可以表示为 y = f(x) + x ,我们知道反向传播的本质是损失函数的链式求导(求导结果的连乘),同时因为参数初始化一般接近于0,这样在训练的过程中更新浅层网络的参数时,很容易随着网络的深入而导致梯度消失,浅层的参数无法更新。但是,观察新的前向传播函数 y = f(x) + x ,你会发现求导结果是 1 + f'(x),也就是说无论f'(x)多么的小,因为1的存在,链式求导的结果不会为0,进而解决了梯度消失的问题。
补充:前些日子在面试CV岗位,也被问到了类似的问题,上述答案基本上是正确的,但是面试官进一步问了如果前向传播进一步改为 y = f(x) + α * x ,如果α特别小,会有什么问题?特别大那?后来我想了想,应该是这样的,还是在求梯度链式求导的时候,求导结果变成了 α + f'(x),当 α 特别小,其实相当于没加这一项,还是有可能出现梯度消失;当 α 特别大,很容易出现梯度爆炸(求导结果会很大,而且还是连乘)。 这里是我个人的理解,有问题的话,欢迎各位一起学习。
6. 本文博主尚未理解的问题?
(1)残差结构能解决梯度爆炸吗?
(2)解决退化问题还有没有更精细或者其他的解释?
(3)普通网络梯度反向传播中![]() 的数值是怎么计算的(后续可能会跟进更新)
的数值是怎么计算的(后续可能会跟进更新)
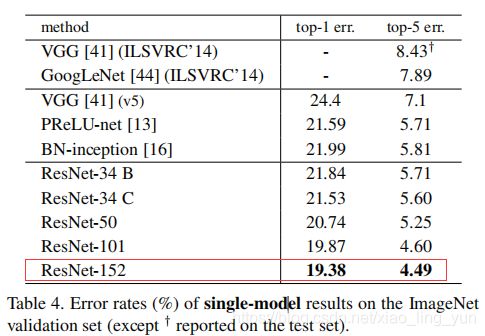
放在最后,上述1到5其实原论文还有很多细节,有需求的可以自己去看看,或者说出来大家一起学习!,对于6中的问题,我可能会后续更新,这个看时间和需求。可能后续会简单写下ResNet2和ResNEXT的博客,但是核心的还是ResNet残差的这种思想,真的牛皮!论文的实验结果,你们也可以去直接看看原论文,反正是实验证明了152层的ResNet效果更好(减轻了退化,使得深层网络性能能进一步增强),给你们简单放个图: