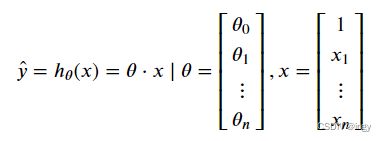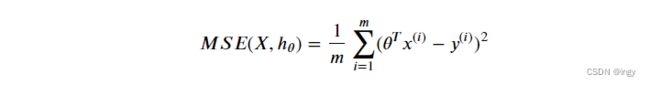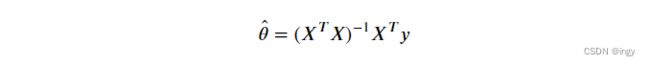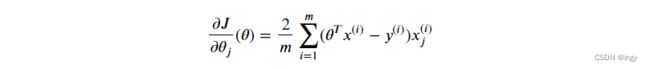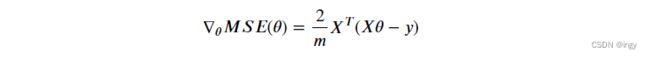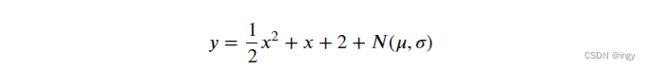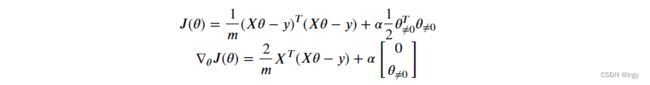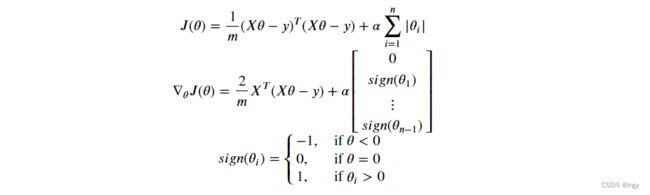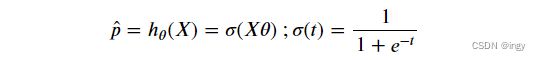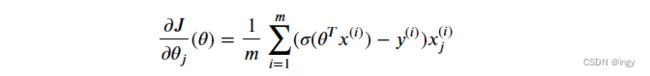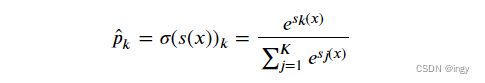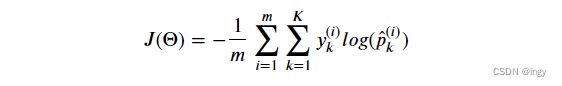【ML笔记】4、训练模型（线性回归、逻辑回归、多类别逻辑回归）

目录

1、线性回归

2、正规方程（The Normal Equation）

3、梯度下降

4、批量梯度下降(BGD)

5、随机梯度下降(SGD)

6、小批量梯度下降(Mini-BGD，MBGD)

7、多项式回归

8、学习曲线

9、线性模型的正则化

Ridge回归（岭回归）

Lasso回归

Elastic Net（弹性网络）

早期停止法（Early Stopping）

10、逻辑回归

逻辑回归的损失函数

策略边界

11、Softmax回归

---

在许多情况下，我们需要了解机器学习算法的内部实现，理解机器学习算法的基本逻辑将帮助我们找到恰当的机器学习模型，合适的训练算法，以及一个好的假设集。且对于理解神经网络是必不可少的。

两个不同的角度研究线性回归训练，即两种不同的训练方法来得到模型的最优解:

• 采用直接“闭式”分析方法，得到线性模型的最优参数。
• 使用一种叫做梯度下降（GD）的迭代优化方法。逐渐调整模型参数得到最小的损失函数，最终参数会收敛到和第一种方法相同的的值。我们将看到多种类型的梯度下降：随机GD、批量GD、小批量GD。这些梯度下降方法在网络模型的使用中非常重要。

1、线性回归

一个最简单的线性回归问题，幸福感推理模型：

_=0+1×__

这个模型仅仅是输入量 GDP_per_capita的线性函数，0和1是这个模型的参数，线性模型更
一般化的描述指通过计算输入变量的加权和，并加上一个常数偏置项来得到一个预测值。

̂ =0+11+22+⋯+

̂表示预测结果
n表示特征的个数
xi表示第 i 个特征的值
j表示第 j 个参数（包括偏置项0和特征权重值1、2、....、n）

可以写成更为简洁的向量形式 

h表示参数为的假设函数。

在机器学习中，向量被视作列数组，和x都是列数组，所以也可以将输出̂看作是矩阵的乘：

训练一个模型意味着调整参数，使模型最好的拟合数据。首先需要描述什么是“最佳拟合数据”，选择均方误差()作为模型性能的衡量标准:

 2、正规方程（The Normal Equation）

为了找到最小化损失函数的值，可以采用公式解，就是可以通过解正规方程直接得到最后的结果

 输出就是使损失函数最小的值。

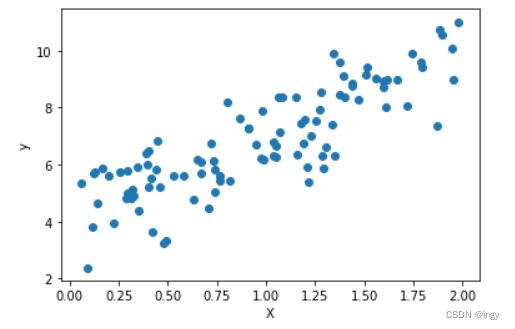
以下代码用于随机生成原始实例，并在画布上画出原始实例： 

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('default') 

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1) 

plt.scatter(x=X, y=y)
plt.xlabel('X')
plt.ylabel('y')
plt.show() 

 现在计算使损失函数最小的θ。

X_b = np.c_[np.ones_like(X), X]

theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best 

可以看到，由于存在噪声，参数不可能达到到原始函数的值，但是很接近。

3、梯度下降

梯度下降是一种非常通用的优化算法，它能够很好地解决一系列问题。梯度下降的整体思路是通过的迭代来逐渐调整参数使得损失函数达到最小值。
假设浓雾下，你迷失在了大山中，你只能感受到自己脚下的坡度。为了最快到达山底，一个最好的方法就是沿着坡度最陡的地方下山。这其实就是梯度下降所做的：它计算误差函数关于参数向量的局部梯度，同时它沿着梯度下降的方向进行下一次迭代。当梯度值为零的时候，就达到了误差函数最小值 。
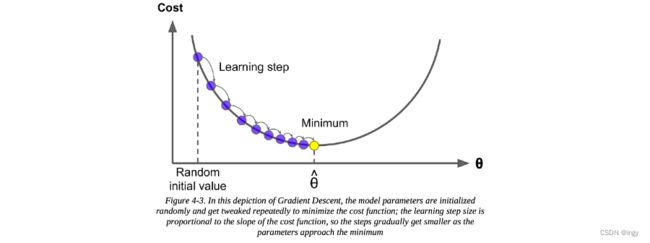
具体来说，开始时，需要选定一个随机的（这个值称为随机初始值），然后逐渐去改进它，每一次变化一小步，每一步都试着降低损失函数（例如：均方差损失函数） ，直到算法收敛到一个最小值。

梯度下降中一个重要的参数是步长，超参数学习率决定了步长的大小。如果学习率太小，必须经过多次迭代算法才能收敛，这是非常耗时的。但如果学习率太大，你将跳过最低点，到达山谷的另一面，这可能使算法是发散的，函数值变得越来越大，永远不可能找到一个好的答案。

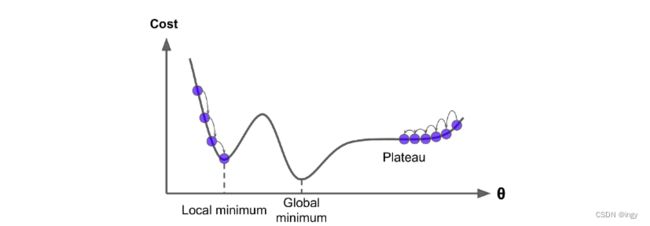
但并不是所有的损失函数看起来都像一个规则的碗。它们可能是洞，山脊，高原和各种不规则的地形，使它们收敛到最小值非常的困难。如果随机初始值选在了图像的左侧，则它将收敛到局部最小值，这个值要比全局最小值要大。如果它从右侧开始，那么跨越高原将需要很长时间，如果你早早地结束训练，你将永远到不了全局最小值。 

 幸运的是，MSE损失函数对于线性回归的结果是一个凸损失函数，这意味着，它保证找到的最值是函数的全局最小值(没有局部最小值，只有一个全局最小值)。它也是一个连续函数，其斜率永远不会突然变化。

重要的提示：当我们使用梯度下降的时候，应该确保所有的特征有着相近的尺度范围（如sklearn的StandardScaler类），否则它将需要很长的时间才能够收敛。

训练模型意味着找到一组模型参数，这组参数可以在训练集上使得损失函数最小。这是对于模型参数空间的搜索，模型的参数越多，参数空间的维度越多，找到合适的参数越困难。

4、批量梯度下降(BGD)

梯度下降的过程，其实就是计算每一个θj下损失函数的梯度的过程。换句话说，你需要计算当θj变化一点点时，损失函数改变了多少，也就是损失函数对θj的偏导数。

用一个偏导函数公式来定义MSE损失函数：

 MSE损失函数的表达式：

 可以得到MSE损失函数对θj的梯度向量：

左边的梯度向量包含了损失函数所有的偏导数，有了梯度向量，你就不必逐一计算每一个梯度。梯度向量的计算包含了整个训练集X，这也是为什么这个算法称为批量梯度下降：每一次训练过程都使用所有的的训练数据。因此，在大数据集上，其会变得相当的慢。但是梯度下降的运算规模和特征的数量成正比，所以训练一个数千数量特征的线性回归模型使用批量梯度下降要比使用正规方程快的多。
一旦我们有了梯度向量，它指向上坡，我们就沿着相反的方向向下走。

θ减去学习率和梯度向量的积，得到的是梯度下降的步长：

生成实例：

X = np.linspace(start=0, stop=1, num=100)
y = (0.5 * X) + 0.1 + 0.3 * np.random.rand(100)

plt.scatter(x=X, y=y)
plt.show()

 X = np.c_[np.ones_like(X), X]

theta = np.random.rand(2) 

MSE损失函数：

def mse(X, y, theta):
    m = X.shape[0]
    X_theta = np.matmul(X, theta)
    return 1./m * np.matmul((X_theta - y).T, (X_theta - y)) 

MSE损失函数的梯度向量： 

def grad_mse(X, y, theta):
    m = X.shape[0]
    X_theta = np.matmul(X, theta)
    return 2./m * np.matmul(X.T, X_theta - y) 

选择一个学习率

lr = 0.01 

 现在优化模型参数

while mse(X, y, theta) > 0.01:
    theta = theta - lr * grad_mse(X, y, theta) 

最后得到的MSE损失函数结果： 

mse(X, y, theta) 

 检查拟合的模型参数：

theta 

最后画出拟合的线性回归模型 

plt.scatter(x=X[:,1], y=y)
plt.plot([0,1], [theta[0] + theta[1]*0, theta[0] + theta[1]*1], color='red')
plt.show()

选取迭代次数也很重要，如果太小了，当算法停止的时候，你依然没有找到最优解。如果太大了，算法会非常的耗时同时后来的迭代参数也不会发生改变。一个简单的解决方法是：设置一个非常大的迭代次数，但是当梯度向量变得非常小的时候，结束迭代。
非常小指的是：梯度向量小于一个值 （称为容差） 。这时候可以认为梯度下降几乎已经达到了最小值。

5、随机梯度下降(SGD)

批量梯度下降的最要问题是计算每一步的梯度时都需要使用整个训练集。与其完全相反的随机梯度下降，在每一步的梯度计算上只随机选取训练集中的一个样本。很明显，由于每一次的操作都使用了非常少的数据，这样使得算法变得很快。

另一方面，由于它的随机性，与批量梯度下降相比，其呈现出更多的不规律性：它到达最小值不是平缓的下降，损失函数会忽高忽低，只是在大体上呈下降趋势。随着时间的推移，它会非常的靠近最小值，但是它不会停止在一个值上，它会一直在这个值附近摆动。因此，当算法停止的时候，最后的参数还不错，但不是最优值。

随机梯度下降算法能够跳过局部最小值，在寻找全局最小值上比批量梯度下降表现要好。虽然随机性可以很好的跳过局部最优值，但同时它却不能达到最小值。解决这个难题的一个办法是逐渐降低学习率。开始时，走的每一步较大（这有助于快速前进同时跳过局部最小值），然后变得越来越小，从而使算法到达全局最小值。决定每次迭代的学习率的函数称为learning schedule。如果学习速度降低得过快，你可能会陷入局部最小值，甚至在到达最小值的半路就停止了。如果学习速度降低得太慢，你可能在最小值的附近长时间摆动，同时如果过早停止训练，最终只会出现次优解。

随机梯度下降的损失函数和梯度的公式如下：

SGD的MSE损失函数： 

 def sgd_loss(X_i, y_i, theta):
    """
    # Arguments:
        X_i, np.ndarray shape=(1,n): the intput training data row vector with `1` in the beginning.
        y, np.ndarray shape=(1,1): the target of the training row.
        theta, np.ndarray shape=(n,1): the parameters vector of the model.
    # Returns
        MSE, float: Mean Squared Error between `X*theta` and `y`.
    """
    X_theta = np.matmul(X_i, theta)
    return (X_theta - y_i)**2

SGD的梯度： 

def grad_sgd_loss(X_i, y_i, theta):
    X_theta = np.matmul(X_i, theta)
    return 2. * X_i.T * (X_theta - y_i) 

学习率下降函数： 

def learning_rate_scheduler(lr, perc):
    return perc * lr

theta = np.random.rand(2) #初始化参数

lr, steps = 0.1, 100000 #初始化学习率，学习步数

for _ in range(steps):
    random_idx = np.random.randint(low=0, high=X.shape[0])
    lr = learning_rate_scheduler(lr, perc=0.99) 
    theta = theta - lr * grad_sgd_loss(X[random_idx], y[random_idx], theta)

 sgd_loss(X[random_idx], y[random_idx], theta)

最后得到的损失函数结果：

以及最后得到的模型参数： 

 theta

 plt.scatter(x=X[:,1], y=y)
plt.plot([0,1], [theta[0] + theta[1]*0, theta[0] + theta[1]*1], color='red')
plt.show()

 拟合的模型并不太好，现在优化SGD的代码如下：

n_epochs = 50
t0, t1 = 5, 50
m = X.shape[0]

def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2, 1)

for epoch in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = X[random_index:random_index+1]
        yi = y[random_index:random_index+1] 
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi) 
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients

 theta

按照惯例，拟合会进行m轮的迭代，每一轮迭代被称为一个epoch。在整个训练集上，随机梯度下降迭代了1000次时，一般在第 50 次的时候就可以达到一个比较好的结果。 

由于每个实例的选择是随机的，有的实例可能在每一代中都被选到，这样其他的实例也可能一直不被选到。如果你想保证每一代迭代过程，算法可以遍历所有实例，一种方法是将训练集打乱重排，然后选择一个实例，之后再继续打乱重排，以此类推一直进行下去。但是这样收敛速度会非常的慢。

sklearn提供了SGDRegressor类来完成线性回归的随机梯度下降，这个类默认优化的是均方差损失函数。下面的代码迭代了1000个epoch，其学习率为0.1（eta0=0.1）：

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1) 

sgd_reg.fit(X=X, y=y) 

sgd_reg.coef_

 拟合的结果与正规方程解很接近。

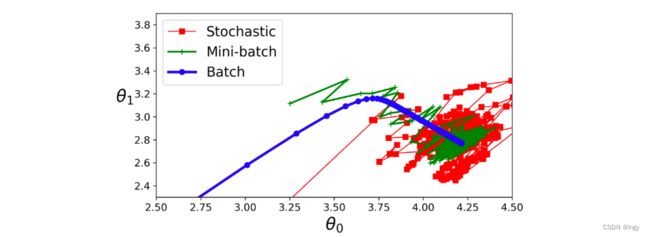
6、小批量梯度下降(Mini-BGD，MBGD)

理解了批量梯度下降和随机梯度下降后，再去理解小批量梯度下降是非常简单的。在迭代的每一步，批量梯度使用整个训练集，随机梯度随机选择实例，在小批量梯度下降中，它则使用一个随机的小型实例集。它比随机梯度的主要优点在于你可以通过矩阵运算的硬件优化得到一个较好的训练表现，尤其当你使用GPU进行运算的时候。

上图显示了参数空间中的梯度下降过程，可见BGD会在损失函数最小的时候停止，但是SGD和MBGD则没有停止梯度下降的过程，结合BGD的收敛过程的时间较长，其实三种梯度下降各有优劣，要视具体的项目需求选择特定的梯度下降。（况且，在一个比较好的学习率下降函数的情况下，SGD和MBGD也可以很好的找到损失函数的全局最小值）。

正规方程和三种梯度下降的性能对比，其中m表示训练样本的个数，n表示特征的个数：

算法	Large m	大批量支持	Large n	超参数个数	缩放要求	sklearn
正规方程	快	不支持	慢	0	无	LinearRegressor
BGD	慢	不支持	快	2	有	N
SGD	快	支持	快	≥2	有	SGDRegressor
MBGD	快	支持	快	≥2	有	N

7、多项式回归

如果数据实际上比简单的直线更复杂呢？ 一个简单的方法是对每个特征进行加权后作为新的特征，然后训练一个线性模型在这个扩展的特征集。 这种方法称为多项式回归。

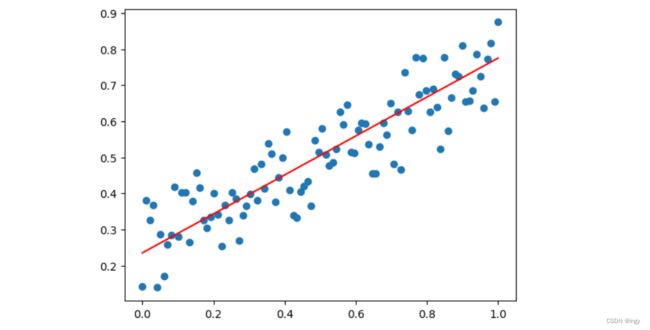
首先，我们根据一个简单的二次方程（并加上一些噪声）来生成一些非线性数据：

m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)

 线性函数是无法拟合出这个模型的，但是可以将x^2作为X的一个新的特征：

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2,include_bias=False)
X_poly = poly_features.fit_transform(X)

X_poly现在包含原始特征X并加上了这个特征的平方X^2。现在你可以在这个扩展训练集上使用 LinearRegression模型进行线性回归拟合。

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_

 拟合得到的曲线为

y = 0.486*x^2 + 1.0648 + 1.95715

8、学习曲线

学习曲线是一种衡量模型拟合性能的方法，画出模型在训练集上的表现，同时画出以训练集规模为自变量的训练集函数。为了得到图像，需要在训练集的不同规模子集上进行多次训练。下面的代码
定义了学习曲线函数，用来画出给定训练集后的模型学习曲线：

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curves(model, X, y):
        X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
        train_errors, val_errors = [], []
        for m in range(1, len(X_train)):
                model.fit(X_train[:m], y_train[:m])
                y_train_predict = model.predict(X_train[:m])
                y_val_predict = model.predict(X_val)
                train_errors.append(mean_squared_error(y_train_predict, y_train[:m]))
                val_errors.append(mean_squared_error(y_val_predict, y_val))
        plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
        plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

上图的曲线表现了一个典型的欠拟合模型，两条曲线都到达高原地带并趋于稳定，并且最后两条曲线非常接近，同时误差值非常大。

首先是训练集的表现：当训练集只有一两个样本的时候，模型能够非常好的拟合它们，这也是为什么曲线是从零开始的原因。但是当加入了一些新的样本的时候，训练集上的拟合程度变得难以接受，出现这种情况有两个原因，一是因为数据中含有噪声，另一个是数据根本不是线性的。因此随着数据规模的增大，误差也会一直增大，直到达到高原地带并趋于稳定，在之后，继续加入新的样本，模型的平均误差不会变得更好或者更差。

第二个是模型在验证集上的表现，当以非常少的样本去训练时，模型不能恰当的泛化，也就是为什么验证误差一开始是非常大的。当训练样本变多的到时候，模型学习的东西变多，验证误差开始缓慢的下降。但是当模型欠拟合的情况下，最后误差会到达在一个高原地带并趋于稳定，最后和训练集的曲线非常接近。

所以，如果你的模型在训练集上是欠拟合的，添加更多的样本是没用的。你需要重新选择一个更复杂的模型或者找到更好的特征来重新训练。

现在来模拟一个过拟合的模型：用10阶多项式来拟合多项式回归中的二次多项式：

from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline((
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("sgd_reg", LinearRegression()),
))
plot_learning_curves(polynomial_regression, X, y)

与欠拟合学习曲线相比，过拟合学习曲线有两个非常重要的不同点：

在训练集上，误差要比线性回归模型低的多。

图中的两条曲线之间有间隔，这意味模型在训练集上的表现要比验证集上好的多，这也是模型过拟合的显著特点。

当然，如果你使用了更大的训练数据，这两条曲线最后会非常接近。

改善模型过拟合的方法是提供更多的训练数据，直到训练误差和验证误差相等。

在统计和机器学习领域有个重要的理论：一个模型的泛化误差由三个不同误差的和决定：

• 偏差：泛化误差的这部分误差是由于错误的假设决定的。例如实际是一个二次模型，你却假设了一个线性模型。一个高偏差的模型最容易出现欠拟合。
• 方差：这部分误差是由于模型对训练数据的微小变化较为敏感，一个多自由度的模型更容易有高的方差（例如一个高阶多项式模型） ，因此会导致模型过拟合。
• 不可约误差：这部分误差是由于数据本身的噪声决定的。降低这部分误差的唯一方法就是进行数据清洗（例如：修复数据源，修复坏的传感器，识别和剔除异常值）。

9、线性模型的正则化

降低模型的过拟合的好方法是正则化这个模型：模型有越少的自由度，就越难以拟合数据。例如，正则化一个多项式模型，一个简单的方法就是减少多项式的阶数。
对于一个线性模型，正则化的典型实现就是约束模型中参数的权重。接下来我们将介绍三种不同约束权重的方法：Ridge回归，Lasso回归和Elastic Net。

Ridge回归（岭回归）

Ridge回归是线性回归的正则化版：在损失函数上直接加上一个正则项，这使得学习算法不仅能够拟合数据，而且能够使模型的参数权重尽量的小。注意到这个正则项只有在训练过程中才会被加到损失函数。当得到完成训练的模型后，我们应该使用没有正则化的测量方法去评价模型的表现。
Ridge回归的损失函数和梯度公式：

超参数α用于量化线性回归的正则程度，如果α=0那此时的岭回归就变为线性回归，如果阿尔法非常的大，所有的权重最后都接近于零，最后结果将是一条穿过数据平均值的水平直线。

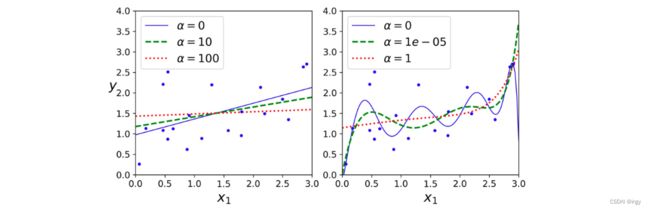
我们应该在岭回归之前进行特征缩放，因为Ridge回归对每个权重的值都很敏感。下面的示例显示了使用不同值在相同线性数据上训练的几个模型，以及Ridge回归正则化的多项式回归：

 与线性回归一样，我们可以通过计算封闭方程或使用梯度下降来执行岭回归：

 用scikit-learn做解封闭方程的Ridge回归：

from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
array([[ 1.55071465]]

作为对比，使用岭回归正则化的SGD梯度下降做线性回归，penalty参数指的是正则项的惩罚类型，指定“l2”表明你要在损失函数上添加一项：权重向量l2范数平方的一半。

sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])

Lasso回归

另一种正则化版的线性回归，就像岭回归那样，它也在损失函数上添加了一个正则化项，但是它
使用权重向量的l1范数而不是权重向量l2范数平方的一半：

Lasso回归的一个重要特征是它倾向于完全消除不重要的特征的权重（即将它们设置为零），自动执行特征选择。在某种意义上，我们可以得到重要的特征。例如右图中的虚线（10e-7），曲线看起来像一条二次曲线，而且几乎是线性的，这是因为所有的高阶多项特征都被设置为零。

下面是一个使用 Scikit-Learn的Lasso类的例子，也可以使用SGDRegressor(penalty="l1")来代替它

from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]]) 

Elastic Net（弹性网络）

是Lasso和Ridge回归混合的一种正则化线性回归，可以控制两种正则化的混合比例r，=0, 变为Ridge回归，=1, 变为Lasso回归：

 三种回归的选择应该视具体场合而定，岭回归是一个很好的首选项，但是如果你的特征仅有少数是真正有用的，你应该选择Lasso和弹性网络，能够将不重要特征的权重降为零。一般来说，弹性网络的表现要比Lasso好，因为当特征数量比样本的数量大的时候，或者特征之间有很强的相关性时，Lasso可能会表现的不规律（把一些重要的特征权重降为0）。

下面是一个使用Scikit-Learn ElasticNet的实例： 

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])

早期停止法（Early Stopping）

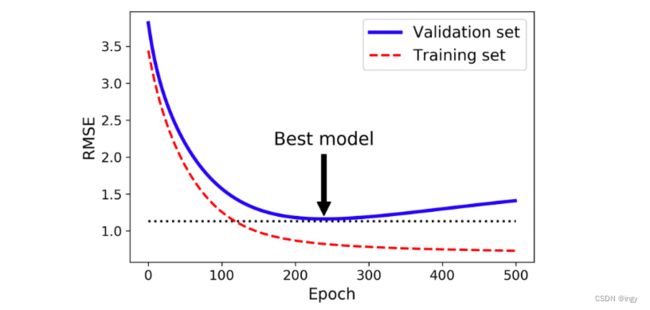
一种非常特殊的正则化方法，梯度下降在验证错误达到最小值时立即停止训练，我们称为早期停止法。随着训练的进行，模型在训练集上的预测误差自然而然的下降。然而一段时间后，验证误差停止下降，并开始上升，这意味着模型在训练集上开始出现过拟合。一旦验证错误达到最小值，便提早停止训练。

需要注意的是，随机梯度下降和小批量梯度下降都不是平滑曲线，你可能很难知道它是否达到最小值。一种解决方案是，只有在验证误差高于最小值一段时间后（确信该模型变得够好了），才停止，之后将模型参数回滚到验证误差最小值。

from sklearn.base import clone
sgd_reg = SGDRegressor(n_iter=1, warm_start=True, penalty=None,learning_rate="constant"
, eta0=0.0005)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
        sgd_reg.fit(X_train_poly_scaled, y_train)
        y_val_predict = sgd_reg.predict(X_val_poly_scaled)
        val_error = mean_squared_error(y_val_predict, y_val)
        if val_error < minimum_val_error:
                minimum_val_error = val_error
                best_epoch = epoch
                best_model = clone(sgd_reg)

10、逻辑回归

逻辑回归用于判断某个实例属于某个的分类的概率，就像线性回归模型一样，逻辑回归模型计算输入特征的加权和（加上偏差项），但它不像线性回归模型那样直接输出结果，而是把结果输入logistic()函数进行二次加工后输出。

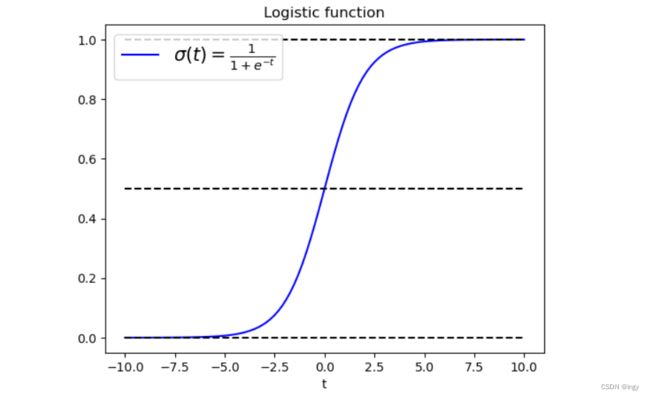
Logistic函数是一个sigmoid函数（图像呈S型，也叫S型函数），它的输出是一个介于0和1之间的数字。

当t<0时σ<0.5，当t≥0时σ≥0.5，因此当Xθ是正数的话，逻辑回归模型输出1，如果是负数的话，则输出0。

sigma_x = np.linspace(start=-10., stop=10., num=100)

def sigmoid(x):
    return 1/(1 + np.exp(-x))

sigma_y = sigmoid(sigma_x)

plt.plot(sigma_x, sigma_y, color='blue', label=r'$\sigma(t)=\frac{1}{1 + e^{-t}}$')
plt.plot([-10, 10], [1/2, 1/2], '--', color='black')
plt.plot([-10, 10], [1, 1], '--', color='black')
plt.plot([-10, 10], [0, 0], '--', color='black')
plt.xlabel('t')
plt.legend(loc='upper left', fontsize=15)
plt.title('Logistic function')
plt.show()

逻辑回归的损失函数

现在我们知道了逻辑回归模型是如何估计概率并做出预测的，但它是如何训练的呢？

训练的目标是得到参数向量，使得预测正面实例的概率高，负面实例的概率低。我们可以通过以下损失函数来理解：

• −()趋于无穷大（当t→0）: 将正例标记为负例，高损失。
• −(1−)趋于无穷大（当→1）: 将负例标记为正例，高损失。
• −()趋于0（当→1）: 正确标记正例，低损失。
• −(1−)趋于0（当→0）: 正确标记负例，低损失。

坏消息是，逻辑回归的损失函数对于求解最小化损失函数的θ是没有公式解的（没有等价的正规方程）。但好消息是，这个损失函数是凸函数，所以梯度下降（或任何其他优化算法）一定能够找到全局最小值（如果学习速率不是太大，并且你等待足够长的时间），损失函数对θ的偏导：

策略边界

以iris数据集为例，让我们尝试建立一个分类器，仅仅使用花瓣的宽度特征来识别Virginica类的鸢尾花，首先让我们加载数据：

from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
X = iris["data"][:, 3:] # petal width
y = (iris["target"] == 2).astype(np.int)

接下来，我们训练一个逻辑回归模型：

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)

我们来看看模型估计的花瓣宽度从0到3厘米的概率估计：

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris-Virginica")

Virginica花的花瓣宽度在1.4 cm到2.5 cm之间，而其他种类的花通常从0.1 cm到1.8 cm。在大约2cm以上时，分类器非常肯定这朵花是Virginica花，而在1厘米以下时，它非常肯定这朵花不是Virginica花。在这两个极端之间，分类器是不确定的。但是，如果你使用它进行预测（使用predict()方法），它将返回一个最可能的结果。因此，在1.6厘米左右存在一个决策边界，这时两类情况出现的概率都等于50%：如果花瓣宽度大于1.6 厘米，则分类器将预测该花是Virginica，否则预测它不是（即使它有可能错了）。

log_reg.predict([[1.7], [1.5]])

下图显示了相同的决策边界，但用了两个特征：花瓣长度和花瓣宽度。彩色线表示训练后的逻辑回归函数的置信概率相关的边界：

11、Softmax回归

Logistic回归模型可以直接推广到支持多类别分类，称为Softmax回归或多类别Logistic回归。
这个想法很简单：当给定一个实例X时，Softmax回归模型首先计算k类的分数Sk(X)，然后将分数应用在Softmax函数（也称为归一化指数）上，估计出每类的概率。

计算Sk(X)的公式：

Softmax函数用于估计出样本属于第k类的概率：

• K表示有多少类
• s(x)表示得分向量
• σ(s(x))k：表示给定每一类得分后，实例x属于k类的概率

和逻辑回归分类器一样，Softmax回归分类器将估计概率最高的那类作为预测结果

这个函数返回σ(s(x))k最大的时候的k值，也就是对应的类。

训练目标是建立一个模型，在目标类别上有着较高的概率（其他类别的概率较低），最小化公式

这个Softmax回归的损失函数称为交叉熵，与逻辑回归相似，当模型对目标类得出了一个较低的概率，会惩罚这个模型。即，交叉熵用于衡量待测类别与目标类别的匹配程度。

可见，当只有两个类时（k=2），此损失函数就是Logistic回归的损失函数。

k类交叉熵的梯度向量：

你可以计算每一类的梯度向量，然后使用梯度下降（或者其他的优化算法）找到使得损失函数达到最小值的参数矩阵。

使用iris来做三分类：

X = iris['data'][:, (2,3)]  # Petal Length & Width
X.shape
y = iris['target']
softmax_reg = LogisticRegression(multi_class='multinomial', solver='lbfgs', C=10)
softmax_reg.fit(X, y)

softmax_reg.predict([[5,2]]) 

(softmax_reg.predict_proba([[5,2]])*100).astype(int)

所以你发现一个花瓣长为5厘米，宽为2厘米的鸢尾花时，你可以问你的模型你它是哪一类鸢尾花，它会回答94%是Virginica花（第二类），或者5%是其他鸢尾花。