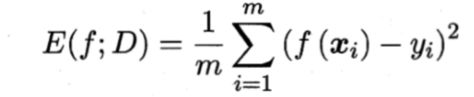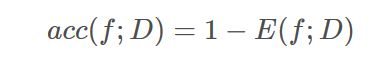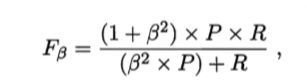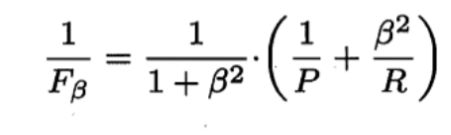ML笔记（2）模型评估与选择

2.1 经验误差与过拟合

• 错误率(error rate)：分类错误的样本数占样本总数的比例。

• 精度(accuracy)：精度 = 1 - 错误率（常常以百分比的形式书写）

• 误差(error)：实际预测输出与样本的真实输出之间的差异。

• 训练误差(training error)/经验误差(empirical error)：学习器在训练集上的误差。

• 泛化误差(generalization error)：新样本/测试集上的误差。

我们实际希望得到的是从新样本上能表现得很好的学习器，即泛化误差小。为了达到这个目的，应该从训练样本中尽可能学出适用于所有潜在样本的“普遍规律”。

学习器把训练样本学得太好了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质。称之为“过拟合”(overfitting)。相对地，还没有学好训练样本中的一般性质称为“欠拟合”(underfitting)。

2.2 评估方法

通过实验测试来对学习器的泛化误差进行评估并进而做出选择。为此，需要使用一个"测试集"(testing set)来测试学习器对新样本的判别能力，然后以测试集上的测试误差(testing error)来作为泛化误差的近似。

1. 留出法
简单来说就是将样本分成互斥的两个集合，将其中一个作为训练集，另外一个作为测试集。
需要注意的是：在划分数据集时应保持数据的一致性。如分类任务中训练集和测试集的样本应保持相同比例。
为了减少分割方式带来的差异，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果

2. 交叉验证法
先将数据集D划分为k个大小相似的互斥子集并尽可能保持数据分布的一致性（分层采样）。然后每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集。这样就获得了kk组的训练集和测试集，然后就进行k次训练。
返回的是k个测试结果的均值。交叉验证法评估结果的稳定性和保真性很大程度上取决于k的取值。

一般K的取值为10，考虑到数据大小不同，K值的范围可大可小。

3 自助法(bootstrapping)
有放回的拿取m个样本，根据极限计算存在36.8%的样本未出现在取出样本中。

优点：

• 自助法在数据集比较小，难以有效划分训练/测试集的时候很有用。

• 能够从初始数据集中产生多个不同的数据集。对集成学习等方法有很大好处。

缺点：

• 自助法产生的数据集改变了初始数据集的分布，引入了估计偏差。

• 初始数据足够的情况下，留出法和交叉验证法更常用一些。

2.3 调参与最终模型

学习算法的很多参数都是在范围内取值，因此对每种参数配置都训练出模型来是不可行的。

现实中常用的做法是对每个参数选定一个范围和变化步长。eg: 在[0,0.2]范围内以0.05为步长，则实际要评估的候选参数数值有5个。这是在计算开销和性能估计之间进行折中的结果。

这里提一句，在调参的过程中可能同时调整很多超参数。如KNN算法中的P，N。通常情况下回使用网格搜索（gridsearch）sklearn中使用的库是gridsearchCV，CV就是交叉验证的意思。

2.4性能度量

这是对模型泛化能力的评价，不同的模型有不同的评价标准。

2.4.1 错误率与精度

1.回归任务的评价标准：均方误差

这个是预测值和真实值差的平方再开个根号，也就是我们常说的R方值。

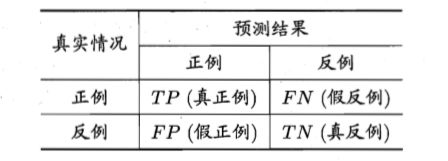
2.分类任务
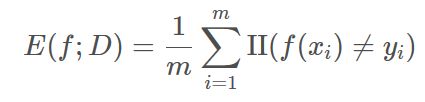这里II是一个指示函数，相等时返回1，不相等时返回0
通俗来说就是：分类错误的样本数/总样本数

分类精度：

2.4.2查准率、查全率

查准率：记号为P，是真正例在所有预测为正例（真正例+假正例）中的比率。
查全率：记号为R，是真正例在所有真实为正例（真正例+假反例）中的比率。
查准率和查全率是一对矛盾量，在假正例和假反例为一定水平的条件下，增大查准率会减小查全率，增大查全率会减小查准率。
P-R反向关系原理
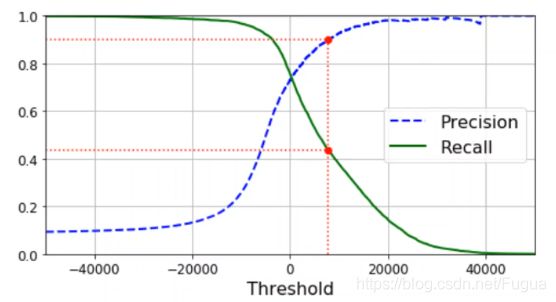
下图是一个手写识别的例子（预测是否为5）

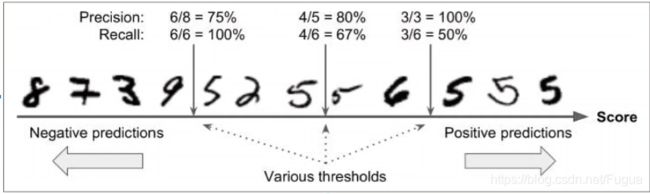
在这个二分类问题中，模型在分类时往往是确定一个阈值，大于这个阈值的被预测为5，小于这个阈值的被预测为非5。
上述三个箭头表示模型的阈值，当阈值改变时，P-R是同时改变的，改变的方向是相反的。
这里阈值的确定是由模型的参数确定的，可以为人改变。

由此可以得出以下的P-R关系图：

2.4.3 阈值的评估

一种训练集的阈值可以由模型的参数确定，当然不同的模型也会有不同的阈值。
阈值作为模型判断分类的依据，我们通常有以下方法评估阈值。

1. BEP
   BEF就是P-R曲线中的平衡点
   
   2. F1
      $$\frac{1}{F1}=\frac{1}{2}\times \frac{1}{\frac{1}{P}+\frac{1}{R}}$$
      这里F1采用了调和平均数的概念
      化简如下：
      
2. Fβ
   
   其中β是自己调整的参数，β>1时说明查全率有更大的影响，β<1时说明查准率有更大的影响。
   这里采用了加权调和平均的概念
   

2.5 ROC AUC

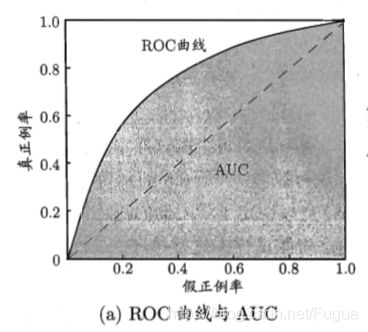
2.5.1 ROC

ROC曲线由TPR（真正例率）和FPR（假正例率）组成
此时TPR和FPR是同向变化的，当我们使用不同模型时我们会得到两条ROC曲线。我们希望在相同的FPR下，选择TPR相对更高的模型

我们将ROC的面积表示为AUC

2.5.2 AUC

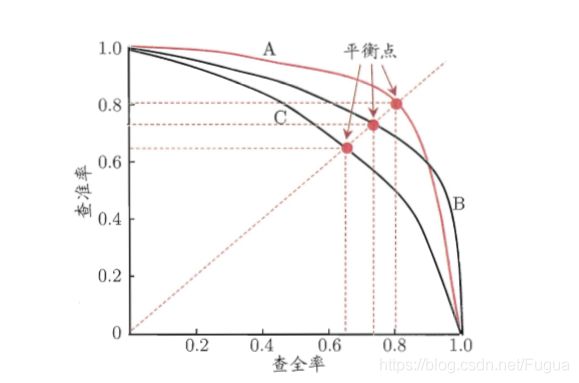
当我们使用不同的模型进行评价，如果其中一个ROC曲线A包裹了另一条ROC曲线B，那么我们认为A模型最佳。
假如AB曲线由相交的地方，则我们考虑两者的面积，即AUC

此处公式较多，例子比较复杂不方便具体说明，此视频中有详细介绍

2.6 代价曲线

非均等代价：对不同类型错误赋予不同权重损失所计算出来的代价。
代价敏感错误率：不同错误类型个数乘以对应代价，求总和后除以总样本数m。综合表现了分类器性能以及度量的偏好。
正概率代价：记p为样例为正的概率，则正概率代价P+cost等于正例概率p与假反代价的积除以代价总和（假正代价+假反代价）。以正例概率p作为自变量，是分类阈值变动的量化。考虑假正代价和假反代价的比值，与具体值无关。
归一化代价：见书上公式2.25。
代价曲线：以正概率代价做横轴，归一化代价为纵轴。以样例为正概率p为自变量，取ROC曲线上每一点计算FPR和FNR（FNR=1-TPR）绘制线段，所有线段的公共下界就是代价曲线，所围成的面积就是总体期望代价。总体期望代价反映了学习器在所有条件下的总代期望，越小分类性能越好。当p=0时，假正率为0，代价总体期望最小为0，不关心假反率，因为没正例。当p=1时，总体期望代价最小为0，不关心假正率，因为没有反例。

这块内容有点抽象，知乎高票回答中的篮球例子比较好理解，例子点这

2.7 比较检验

• 假设检验：对某个未知参数做出假设，这个未知参数通常是总体样本集的某个参数，但是我们没办法获得（比如一批灯泡的平均使用寿命）。给出显著度α，在假设的前提下，求出满足显著度和假设的置信区间，然后对比被假设参数是否在置信区间内：在，接受假设；不在。拒绝假设。
• 假设检验假设：假定测试样本是从样本总体分布中独立采样而得。
• 对泛化错误率使用假设检验：第一步：假设泛化错误率ε<=ε0，给出显著度α。第二步：求出在满足泛化错误率ε=ε0、显著度为α的条件下最大临界错误率ε_hate。第三步：判断实际测试错误率和临界错误率ε_hate关系，来看是否接受假设。
• 二项检验：适用单个学习器单次检验。假定测试样本是从样本总体分布中独立采样而得。采用假设为ε=ε0。变量二项分布。
• t检验：适用单个学习器多次重复的检验。假定测试样本是从样本总体分布中独立采样而得。采用假设为ε=ε0。变量t分布。
• k折交叉验证成对t检验：适用两个学习器性能对比检验。是t检验在k折交叉验证上的应用。假定测试样本是从样本总体分布中独立采样而得。采用假设为各学习器性能相同。变量t分布。
• 5x2交叉验证：独立采样假设不成立。做5次2折交叉验证，是k折交叉验证的变形。采用假设为各学习器性能相同。变量t分布。
• McNemar检验：适用比较两个二分类学习器的性能。采用假设为各学习器性能相同。变量χ2分布。
• Friedman检验：适用多个学习器性能检验。采用假设为各学习器性能相同。当假设被拒绝时，采用后续检验进一步区分各个算法性能，比如Nemenyi后续检验。变量F分布
• Nemenyi后续检验：适用比较多个算法性能，配合Friedman检验来进一步区分不同算法性能。采用假设为各个学习器性能相同。变量Tukey分布。