2018-2019 ACM-ICPC, China Multi-Provincial Collegiate Programming Contest（A、B、C、H）

原题 pdf

A. Maximum Element In A Stack（注意，gym 里的题面有误。建议看原题 pdf）

单调栈 维护当前栈中最大值

依据题中给定的函数处理输入，之后就是单调栈经典操作。（一定要进行越界特判啊，不然会 wa的很惨的！）

Preproblem：AcWing 41. 包含min函数的栈（单调栈）

另外，提交选择语言的时候，千万别选 Clang++！

#include <bits/stdc++.h>

using namespace std;
//#define int long long
//#define map unordered_map
#define ll long long

//int128 ORZ

/*
__int128 read() {
	__int128 x = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch>'9') {
		if (ch == '-')f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x * f;
}

void print(__int128 x) {
	if (x < 0) {
		putchar('-');
		x = -x;
	}
	if (x > 9) print(x / 10);
	putchar(x % 10 + '0');
}
*/
const int N = 5e6 + 10;
typedef unsigned long long ull;
typedef unsigned int ui;
int n, p, q, m;
ui SA, SB, SC;
ui s1[N], s2[N];	//别特么自己找麻烦用vector数组，直接上普通数组就好！
int tt1, tt2;

unsigned int rng61()
{
	SA ^= SA << 16; SA ^= SA >> 5; SA ^= SA << 1;

	unsigned int t = SA;

	SA = SB; SB = SC; SC ^= t ^ SA;

	return SC;
}

signed main()
{
	int _ = 1; cin >> _;

	for (int i = 1; i <= _; ++i)
	{
		tt1 = tt2 = 0;

		cin >> n >> p >> q >> m >> SA >> SB >> SC;
		for (int k = 0; k <= n; ++k) s1[k] = s2[k] = 0;
		ll sum = 0;
		int tt1 = 0, tt2 = 0;
		for (int j = 1; j <= n; j++)
		{
			bool ok = (rng61() % (p + q) < p);
			if (ok) {
				auto tmp = rng61() % m + 1;
				s1[++tt1] = tmp;
				if (tt2 == 0) s2[++tt2] = tmp;
				else
				{
					if (tmp >= s2[tt2]) s2[++tt2] = tmp;
				}
			}
			else if(tt1)	//一定要进行越界判断啊，不然会很惨的！
			{
				--tt1;
				if (s1[tt1 + 1] == s2[tt2]) --tt2;
			}
			sum ^= (1ll * j * s2[tt2]);
		}
		printf("Case #%d: %llu\n", i, sum);
	}

	return 0;
}

B - Rolling The Polygon（计算几何 余弦定理 两点距离公式 弧长公式）

题意：

数学题：要求推导出 一个凸多边形在水平面上滚动一周的过程中，其内部某个点 q 移动总距离的数学公式。

题目输入给定了特定的多边形以及其内部一点 q，输出 q 的移动总距离 track。

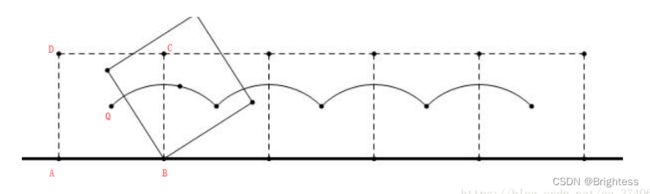
可以直接分析上面的这个例子（以某种情况举例推出一般情况）：

一开始以 B 为圆心 QB 为半径，顺时针转 90°；后以 C 为圆心 QC 为半径，也转 90°；往后同理。

最后一定转了 360°。通过分析这个例子可以看出：

• 在凸多边形 滚动一周 的全程中，分别以 其每个点为圆心，以 这个点（凸多边形的每个顶点）到 Q 距离 作为 半径，以 这个点（凸多边形的每个顶点）所在角 的 补角 作为 每次移动的弧度。

（弧长的计算公式为： 弧长 = 弧度 * 半径）

对于凸多边形某个定点所在角 A，我们可以通过余弦定理算出来：

cosA ＝ (b ^ 2 + c ^ 2 - a ^ 2) / 2bc（b、c 为凸多边形相邻两边，a、b、c 三者共同形成一个三角形，这是余弦定理运用的条件）

因此 A = acos((b ^ 2 + c ^ 2 - a ^ 2) / 2bc)

每次移动的弧度是 A 弧度的补角，可以通过 pi - A 求出。

#include <bits/stdc++.h>

using namespace std;
//#define int long long
//#define map unordered_map

//int128 ORZ

/*
__int128 read() {
	__int128 x = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch>'9') {
		if (ch == '-')f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x * f;
}

void print(__int128 x) {
	if (x < 0) {
		putchar('-');
		x = -x;
	}
	if (x > 9) print(x / 10);
	putchar(x % 10 + '0');
}
*/

typedef double db;
const int N = 55;
const db pi = acos(-1);
int cnt = 0;
int n;
struct Point
{
	db x, y;
} pot[N];
Point q;

db get_dis(Point a, Point b)
{
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

inline void solve()
{
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		cin >> pot[i].x >> pot[i].y;
	}
	cin >> q.x >> q.y;
	
	db track = 0;
	for (int i = 0; i < n; ++i)
	{
		db len = get_dis(pot[i], q);	//每个点到q的距离
		db a = get_dis(pot[(i - 1 + n) % n], pot[(i + 1) % n]);
		db b = get_dis(pot[(i - 1 + n) % n], pot[i]);
		db c = get_dis(pot[(i + 1) % n], pot[i]);
		db ang = pi - acos((b * b + c * c - a * a) / (2 * b * c));	//多边形各个角的补角 这里我们要用弧度的形式
		track += (ang * len);
	}
	
	printf("%.3lf\n", track);
}

signed main()
{
	//	ios::sync_with_stdio(false);
	//	cin.tie(nullptr), cout.tie(nullptr);

	int _ = 1; cin >> _;

	while (_--)
	{
		printf("Case #%d: ", ++cnt);
		solve();
	}

	return 0;
}

C. Caesar Cipher

题意：输入三行字符串，第一行是明文，第二行是密文，这两行规定了明文到密文的转化规则。第三行给出一行密文，要求按照刚刚的规则输出它的明文字符串。

#include <bits/stdc++.h>

using namespace std;
//#define int long long
//#define map unordered_map

//int128 ORZ

/*
__int128 read() {
	__int128 x = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch>'9') {
		if (ch == '-')f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x * f;
}

void print(__int128 x) {
	if (x < 0) {
		putchar('-');
		x = -x;
	}
	if (x > 9) print(x / 10);
	putchar(x % 10 + '0');
}
*/
int n, m;
string s1, s2, s3;
int cnt = 0;

inline void solve()
{
	cin >> n >> m;
	cin >> s1 >> s2 >> s3;
	int tmp = s2[0] - s1[0];	//转化规则
	for(auto &ch : s3)
	{
		ch = (ch - 'A' - tmp + 26) % 26 + 'A';	//密文向明文的转变 这样取模是为了避免模结果为负数的情况
	}
	printf("Case #%d: ", ++cnt);
	cout << s3 << '\n';
}

signed main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(nullptr), cout.tie(nullptr);

	int _ = 1; cin >> _;

	while(_--)
	{
		solve();
	}

	return 0;
}

H. Fight Against Monsters（前缀和 + 二分 + 贪心）

题意：

有一个英雄要打 n 个怪，每个怪有两个属性：HP（血量）、ATK（攻击力）。

对于某一个怪而言，英雄每秒中对它的输出伤害是和时间成正比的，即在攻击这个怪物的第一秒时对它的伤害为 1，第二秒为 2，第三秒为 3，以此类推。

而对于英雄而言，每秒钟都会收到所有 活着的怪物 的攻击。

要求输出英雄承受的最小总伤害。

思路：

对于每个怪物有两个属性：a（血量）、b（攻击力），我们额外增加一个属性 c：ATK / 打败这个怪物要花费的时间（这是个 double 类型的属性）

对于所有怪物，如果属性 c 不相等，我们按照 c 从大到小排序，如果 c 相等，则按照 b 从大到小排序。

之后就模拟英雄打怪的这个过程，求出最终答案即可。

#include <bits/stdc++.h>

using namespace std;
#define int long long
//#define map unordered_map

//int128 ORZ

/*
__int128 read() {
	__int128 x = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch>'9') {
		if (ch == '-')f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	return x * f;
}

void print(__int128 x) {
	if (x < 0) {
		putchar('-');
		x = -x;
	}
	if (x > 9) print(x / 10);
	putchar(x % 10 + '0');
}
*/
const int N = 1e5 + 10;
int n;
int cnt = 0;
typedef pair<int, int> pii;
#define x first
#define y second
int sum[N];
int ttmp[N];

struct node
{
	int a, b;//blood dam
	double c;
} s[N];


bool cmp(struct node aa, struct node bb)
{
	if(aa.c != bb.c) return aa.c > bb.c;
	return aa.b > bb.b;
}

void init()
{
	for (int i = 1; i < N; ++i)
	{
		ttmp[i] = ttmp[i - 1] + i;
	}
}

inline void solve()
{
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		int xx, yy; scanf("%lld%lld", &xx, &yy);
		auto p = lower_bound(ttmp + 1, ttmp + N, xx);
		int tim = p - ttmp;
		s[i] = { xx, yy, 1.0 * yy / tim };
	}
	sort(s + 1, s + n + 1, cmp);
	for (int i = 1; i <= n; ++i)
	{
		sum[i] = sum[i - 1] + s[i].b;
	}
	int hurt = 0;
	int idx = 0;
	for (int i = 1; i <= n; ++i)
	{
		int aa = s[i].b, bb = s[i].a;
		auto p = lower_bound(ttmp + 1, ttmp + N, bb);
		int tim = p - ttmp;
		hurt += tim * (sum[n] - sum[idx]);
		idx++;
	}
	cout << hurt << endl;
}

signed main()
{
	//	ios::sync_with_stdio(false);
	//	cin.tie(nullptr), cout.tie(nullptr);
	init();

	int _ = 1; cin >> _;

	while (_--)
	{
		printf("Case #%d: ", ++cnt);
		solve();
	}

	return 0;
}