强化学习精要-第一部分
文章目录
- 前言
-
- 其他资源
- GYM
-
- GYM down
- GYM introduction
- baselines
- 马尔可夫决策模型
-
- 理论部分
- 代码部分
- 求解
-
- 策略迭代
- 策略迭代 代码
- 效果测试
- 价值迭代
- 两者的共同点
- 广义策略迭代法(结合)
前言
我之前有看过一本《深入浅出强化学习原理》,个人感觉到后面不管是图示还是代码都不清不楚的,但是今天要记录的书本代码清晰,并且文章一看就知道是精心雕琢出来的。在这里做自己的思维导图以及代码讲解,运行效果展示。
作者分了两部分讲解,第一部分是基础,第二部分是开始学习RL的部分。
第一部分包括强化学习的定义与基础知识、数学基础、优化相关知识、tensorflow基本知识、强化学习相关的项目Gym和Baselines
最后介绍了强化学习的基础理论——马尔可夫决策过程以及基于动态规划的求解方法。
下面开始对第一部分的大概介绍
- 在第一部分中,第一二章介绍了强化学习的定义、基础知识、数学基础都比较浅显,能够自己看懂。
其中需要知道的是强化学习的实验环境:
1.Arcade Learning Environment:封装很多Atari2600游戏机游戏的环境
2.Box2D:刚体物理世界仿真
3.MuJoCo:3D物理引擎,仿人任务。
4.Gym:集成平台 - 在第三章介绍了可能用到的优化算法:Gradient Descent、共轭梯度法(这个算法是我没有掌握的,很值得一读,主要解决的问题是GradientDescent中更新每一步的时候并没有在步长方向将所有误差都更新使得剩余误差和此次更新方向正交的问题)以及自然梯度法(也可以一看,因为后面看样子自然梯度法和TRPO算法的提出有一定关系)
- 第四章的tensorflow基本知识比较落后,因为现在出TF2.0了,所以可以跳过,自行去观看2.0相关的API;第五章是关于GYM和baselines的,有必要在下面给出框架介绍和代码解释。
- 第六章介绍基础知识:马尔可夫决策过程以及在简单问题上的两种经典动态规划求解法:策略迭代和价值迭代。这一部分在《深入浅出强化学习原理》的开头也有给出。如果对这一章知识了解透彻,就可以对之后的算法有一个更加透彻的了解(重要)
其他资源
无痛的机器学习:作者的知乎专栏
GYM
官方文档:https://gym.openai.com/docs/
GYM down
这里不做详细介绍,anaconda下好之后新建环境安转gym便可
参见:https://blog.csdn.net/WASEFADG/article/details/81043075
下好之后的测试:
asber@asber-X550VX:~/DRL$ gedit gymtest.py
asber@asber-X550VX:~/DRL$ source activate DRL
(DRL) asber@asber-X550VX:~/DRL$ python gymtest.py
gedit的文件(demo)内容为:
import gym
import time
env = gym.make('CartPole-v0')
env.reset()
env.render()
time.sleep(2)
如果正常会运行两秒的倒立摆静止的画面
GYM introduction
GYM中第一个需要知道的是Env环境对象,使用下面这段话建立环境
import gym
env=gym.make('[game name]')
使用下面这段话查看拥有的环境:
from gym import envs
print(envs.registry.all())
env有三个核心方法
1.reset:重新开始人物,并且将环境设置成任务初始的状态 s 0 s_0 s0
2.step(a):传入参数a表示动作,环境根据行动产生下一刻观测、奖励、任务是否结束等信息(计算-物理引擎)
3.render:输出当前状态(可视化-图像引擎)
import gym
import time
env = gym.make('CartPole-v0') #创造环境
observation = env.reset() #初始化环境,observation为环境状态
count = 0
for t in range(100):
action = env.action_space.sample() #随机采样动作
observation, reward, done, info = env.step(action) #与环境交互,获得下一步的时刻
if done:
break
env.render() #绘制场景
count+=1
time.sleep(0.2) #每次等待0.2s
print(count) #打印该次尝试的步数
env.close()
在强化学习中有两种space,action_space和observation_space,这两个space都隶属于space类,而这个space类分为两种
Box和Discrete,前者描述了连续的空间,后者描述了离散的空间。
import gym
env = gym.make('CartPole-v0')
print(env.action_space)
#> Discrete(2)
print(env.observation_space)
#> Box(4,)
这代表平衡车的动作空间有左右
而状态空间是连续的四维空间
书中还介绍了wrapper类用来对已有的环境进行更改。【之后如果有需要再行了解】
下面给出使用GYM自己写环境的demo:用gym搭建一个蛇行棋的代码
import numpy as np
import gym
from gym.spaces import Discrete
class SnakeEnv(gym.Env):
SIZE=100 # 100 states in total 蛇行棋一共一百格
'''
How Environment build
Args:
(int)ladder_num:number of ladder 多少个梯子
(list)dices:max number every way to throw dice can acheive 扔骰子的方式
Returns:
None
Example:
SnakeEnv(10, [3,6])
Generate 10 ladders randomly and give two ways to throw dice,one can throw out number between 1 and 3,the other one can throw out number between 1 and 6
'''
def __init__(self, ladder_num, dices):
self.ladder_num = ladder_num
self.dices = dices
self.ladders = dict(np.random.randint(1, self.SIZE, size=(self.ladder_num, 2)))
self.observation_space=Discrete(self.SIZE+1)
self.action_space=Discrete(len(dices))
print('ladders info:')
print(self.ladders)
print('dice ranges:')
print(self.dices)
self.pos = 1
'''
Reset Enviroment
Args:
None
Returns:
(int)pos:the initial position of enviroment
Example:
Env.reset()
'''
def reset(self):
self.pos = 1
return self.pos
'''
According given action culculate posible next status and reward and if it's end and other info
Args:
(int)the number which strategy do you choose
Returns:
(int)pos:the next position of enviroment
(int)reward:reward based on status and action
(bool)done:if the game is over
(None){}:infomation-here we do not pass any info
Example:
Env.step(0)
choose first strategy as my action
'''
def step(self, a):
step = np.random.randint(1, self.dices[a] + 1)
self.pos += step
if self.pos == 100:
return 100, 100, 1, {}
elif self.pos > 100:
self.pos = 200 - self.pos
if self.pos in self.ladders:
self.pos = self.ladders[self.pos]
return self.pos, -1, 0, {}
def reward(self, s):
if s == 100:
return 100
else:
return -1
def render(self):
pass
if __name__ == '__main__':
env = SnakeEnv(10, [3,6])
env.reset()
while True:
state, reward, terminate, _ = env.step(0)
print(reward, state)
if terminate == 1:
break
运行结果:
ladders info:
{23: 7, 85: 27, 66: 46, 84: 78, 95: 87, 69: 29, 21: 79, 65: 52, 79: 70, 26: 53}
dice ranges:
[3, 6]
-1 3
-1 5
-1 6
-1 8
-1 10
-1 12
-1 15
-1 17
-1 20
-1 7
-1 9
-1 10
-1 11
-1 13
-1 14
-1 16
-1 18
-1 20
...
-1 98
-1 99
100 100
baselines
书没有对baseline过多细致的描述,只告诉我们这是RL库,以及Baselines开发了很多与Atari游戏有关的环境封装,比如游戏开始前30s随机造作的函数就在baseline的common/_wrappers.py中,这里中对环境跳过30s的操作中就有用到wrapper类
马尔可夫决策模型
理论部分
一次运行可用一条状态-行动链表示:
τ = s 0 , a 0 , s 1 , a 1 , . . . , s t − 1 , a t − 1 , s t \tau = {s_0,a_0,s_1,a_1,...,s_{t-1},a_{t-1},s_t} τ=s0,a0,s1,a1,...,st−1,at−1,st
其中s是状态,a是动作,下标代表时间。
策略是环境 s t s_t st到行动集合上的概率分布(离散行为空间)或者概率密度函数(连续行为空间),行为的评价越高,产生概率越大,那么在时间 t t t,agent的行为准则是
a t ∗ = a r g m a x a t , i p ( a t , i ∣ s 0 , a 0 , . . . , s t ) a_t^*=argmax_{a_{t,i}}p(a_{t,i}|{s_0,a_0,...,s_t}) at∗=argmaxat,ip(at,i∣s0,a0,...,st)意思是在t时刻的动作是在所有 t时刻可做的动作i中概率最大的。
若考虑马尔可夫性,改写成
a t ∗ = a r g m a x a i p ( a i ∣ s t ) a_t^*=argmax_{a_{i}}p(a_{i}|s_t) at∗=argmaxaip(ai∣st)
通过下面的学习可以知道强化学习最优策略的寻找也相当与求解
π ∗ = a r g m a x π υ π ( s ) ∀ s \pi^*=argmax_{\pi} \upsilon_\pi(s) \ \ \ \ \forall s π∗=argmaxπυπ(s) ∀s
而状态的转移也可以用概率表示: p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t) p(st+1∣st,at)
代表在 s t s_t st时刻做出 a t a_t at动作,状态转移到 s t + 1 s_{t+1} st+1的概率,在转移到 s t + 1 s_{t+1} st+1之后会得到奖励 r t r_t rt
所以我们求取策略(行为准则)同等于最大化下面公式
m a x ∑ t r t max \sum_t r_t maxt∑rt
但是假设我们的奖励都是正的没有负数,那么这个公式在时间无限时不容易收敛,公式便易成: m a x ∑ t = 0 γ t r t max \sum_{t=0} \gamma ^t r_t maxt=0∑γtrt
γ \gamma γ的范围在(0,1],可代表每一个状态,agent的死亡概率。
可证明此无限数列和在 γ \gamma γ小于1时收敛。
我们定义另一个量 长期回报:当前状态之后的某次轨迹的所有折扣回报之和
R e t t = ∑ k = 0 γ k r t + k + 1 Ret_t=\sum_{k=0}\gamma^k r_{t+k+1} Rett=k=0∑γkrt+k+1这个量表示某一次轨迹的某个状态之后的回报
而我们知道,状态的转换有时候不能确定,相同状态相同动作到达的下一次状态可能有多种,我们在衡量此次动作的价值的时候,我们就需要考虑之后每一种可能状态的影响,所以需要求的便是状态值函数:已知当前状态 s t s_t st,在某种策略 π \pi π行动下得到所有轨迹 τ \tau τ的长期回报的期望
υ π ( s t ) = E s , a ∼ τ [ ∑ k = 0 γ k r t + k + 1 ] \upsilon _\pi(s_t)=E_{s,a\sim\tau}[\sum_{k=0}\gamma^k r_{t+k+1}] υπ(st)=Es,a∼τ[k=0∑γkrt+k+1]
此处的 s , a ∼ τ s,a \sim \tau s,a∼τ表示, s , a s,a s,a服从 根据 π \pi π得到的 τ \tau τ 的分布
在MDP中值函数不仅有状态值函数还有状态-行为值函数:已知当前状态 s s s和行为 a a a,按照某种策略 τ \tau τ行动产生的长期回报的期望。
q π ( s t , a t ) q _\pi(s_{t},a_{t}) qπ(st,at)
按照期望的定义,状态值函数还可以写为
υ π ( s t ) = E s , a ∼ τ [ ∑ k = 0 γ k r t + k + 1 ] = ∑ τ p ( τ ) ∑ k = 0 ∞ γ k r t + k + 1 \upsilon _\pi(s_t)=E_{s,a\sim\tau}[\sum_{k=0}\gamma^k r_{t+k+1}]=\sum_\tau p( \tau )\sum_{k=0}^\infty\gamma^k r_{t+k+1} υπ(st)=Es,a∼τ[k=0∑γkrt+k+1]=τ∑p(τ)k=0∑∞γkrt+k+1
又因为
τ = s 0 , a 0 , s 1 , a 1 , . . . , s t − 1 , a t − 1 , s t \tau = {s_0,a_0,s_1,a_1,...,s_{t-1},a_{t-1},s_t} τ=s0,a0,s1,a1,...,st−1,at−1,st
p ( τ ) = ∑ ( s 0 , a 0 , . . . ) ∼ τ p ( s 0 ) π ( a 0 ∣ s 0 ) p ( s 1 ∣ s 0 , a 0 ) π ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) . . . p(\tau)= \sum_{(s_0,a_0,...)\sim \tau} p(s_0)\pi(a_0|s_0)p(s_1|s_0,a_0) \pi(a_1|s_1) p(s_2|s_1,a_1)... p(τ)=(s0,a0,...)∼τ∑p(s0)π(a0∣s0)p(s1∣s0,a0)π(a1∣s1)p(s2∣s1,a1)...
所以
υ π ( s t ) = ∑ τ p ( τ ) ∑ k = 0 ∞ γ k r t + k + 1 = ∑ ( s t , a t , . . . ) ∼ τ π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) . . . ∑ k = 0 ∞ γ k r t + k + 1 \upsilon _\pi(s_t)=\sum_\tau p( \tau )\sum_{k=0}^\infty\gamma^k r_{t+k+1}= \sum_{(s_t,a_t,...)\sim \tau} \pi(a_t|s_t)p(s_{t+1}|s_t,a_t)... \sum_{k=0}^\infty\gamma^k r_{t+k+1} υπ(st)=τ∑p(τ)k=0∑∞γkrt+k+1=(st,at,...)∼τ∑π(at∣st)p(st+1∣st,at)...k=0∑∞γkrt+k+1
由于 r t r_t rt与之后的所有状态转移都没有关系(未来的事不能改变过去)所以我们可以通过对上面这个式子转换变成著名的Bellman Equation
υ π ( s t ) = ∑ ( s t , a t , . . . ) ∼ τ π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) . . . ∑ k = 0 ∞ γ k r t + k + 1 = ∑ ( s t , a t , . . . ) ∼ τ π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) . . . [ r t + 1 + ∑ k = 1 ∞ γ k r t + k + 1 ] = ∑ ( s t , a t , . . . ) ∼ τ π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) [ r t + 1 + ∑ ( s t + 1 , a t + 1 , . . . ) ∼ τ ′ π ( a t + 1 ∣ s t + 1 ) p ( s t + 2 ∣ s t + 1 , a t + 1 ) . . . ∑ k = 1 ∞ γ k r t + k + 1 \upsilon _\pi(s_t)= \sum_{(s_t,a_t,...)\sim \tau} \pi(a_t|s_t)p(s_{t+1}|s_t,a_t)... \sum_{k=0}^\infty\gamma^k r_{t+k+1} \\ = \sum_{(s_t,a_t,...)\sim \tau} \pi(a_t|s_t)p(s_{t+1}|s_t,a_t)... [r_{t+1} + \sum_{k=1}^\infty\gamma^k r_{t+k+1}]\\ = \sum_{(s_t,a_t,...)\sim \tau} \pi(a_t|s_t)p(s_{t+1}|s_t,a_t) [r_{t+1} +\sum_{(s_{t+1},a_{t+1},...)\sim \tau'} \pi(a_{t+1}|s_{t+1})p(s_{t+2}|s_{t+1},a_{t+1})... \sum_{k=1}^\infty\gamma^k r_{t+k+1} υπ(st)=(st,at,...)∼τ∑π(at∣st)p(st+1∣st,at)...k=0∑∞γkrt+k+1=(st,at,...)∼τ∑π(at∣st)p(st+1∣st,at)...[rt+1+k=1∑∞γkrt+k+1]=(st,at,...)∼τ∑π(at∣st)p(st+1∣st,at)[rt+1+(st+1,at+1,...)∼τ′∑π(at+1∣st+1)p(st+2∣st+1,at+1)...k=1∑∞γkrt+k+1
下一时刻状态值函数:
υ π ( s t + 1 ) = ∑ ( s t + 1 , a t + 1 , . . . ) ∼ τ π ( a t + 1 ∣ s t + 1 ) p ( s t + 2 ∣ s t + 1 , a t + 1 ) . . . ∑ k = 1 ∞ γ k r t + k + 1 \upsilon _\pi(s_{t+1})= \sum_{(s_{t+1},a_{t+1},...)\sim \tau} \pi(a_{t+1}|s_{t+1})p(s_{t+2}|s_{t+1},a_{t+1})... \sum_{k=1}^\infty\gamma^k r_{t+k+1} υπ(st+1)=(st+1,at+1,...)∼τ∑π(at+1∣st+1)p(st+2∣st+1,at+1)...k=1∑∞γkrt+k+1
所以得到BELLMAN EQUATION
υ π ( s t ) = ∑ a t π ( a t ∣ s t ) ∑ s t + 1 p ( s t + 1 ∣ s t , a t ) [ r t + 1 + υ π ( s t + 1 ) ] \upsilon _\pi(s_{t}) = \sum_{a_t} \pi(a_t|s_t) \sum_{s_{t+1}}p(s_{t+1}|s_t,a_t) [r_{t+1} +\upsilon _\pi(s_{t+1})] υπ(st)=at∑π(at∣st)st+1∑p(st+1∣st,at)[rt+1+υπ(st+1)]
状态值函数同理可得:
q π ( s t , a t ) = ∑ s t + 1 ∑ a t + 1 π ( a t + 1 ∣ s t + 1 ) p ( s t + 1 ∣ s t , a t ) [ r t + 1 + q π ( s t + 1 , a t + 1 ) ] q _\pi(s_{t},a_{t}) = \sum_{s_{t+1}}\sum_{a_{t+1}}\pi(a_{t+1}|s_{t+1})p(s_{t+1}|s_t,a_t) [r_{t+1} +q _\pi(s_{t+1},a_{t+1})] qπ(st,at)=st+1∑at+1∑π(at+1∣st+1)p(st+1∣st,at)[rt+1+qπ(st+1,at+1)]
PS:不同时刻遇到相同状态,值函数相同——时间无关性
代码部分
实现一个表格式的agent,这个agent天生知道以下信息:
1.状态空间的大小s_len
2.动作空间的大小a_len
3.每一个状态的奖励r
4.策略pi 上文中的 ( π \pi π)
状态转移的条件概率分布 p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t) p(st+1∣st,at)通过【梯子的完整信息(这样可以得知下一步准确到达的位置)】以及【已知策略】,对每一个【已知策略】在每一步都去估计下一位子的概率
class TableAgent(object):
def __init__(self, env):
self.s_len = env.observation_space.n
self.a_len = env.action_space.n
self.r = [env.reward(s) for s in range(0, self.s_len)]
self.pi = np.array([0 for s in range(0, self.s_len)])#最初始的策略(之后要迭代变化)
self.p = np.zeros([self.a_len, self.s_len, self.s_len], dtype=np.float)
ladder_move = np.vectorize(lambda x: env.ladders[x] if x in env.ladders else x)
for i, dice in enumerate(env.dices):
prob = 1.0 / dice
for src in range(1, 100):
step = np.arange(dice)
step += src
step = np.piecewise(step, [step > 100, step <= 100],
[lambda x: 200 - x, lambda x: x])
step = ladder_move(step)
for dst in step:
self.p[i, src, dst] += prob
self.p[:, 100, 100]=1
self.value_pi = np.zeros((self.s_len))
self.value_q = np.zeros((self.s_len, self.a_len))
self.gamma = 0.8
def play(self, state):
return self.pi[state]
求解
通过上面的建模,我们了解到,强化学习的目标就是找到最优的策略,可以使的每一个状态值函数最大化 π ∗ = a r g m a x π υ π ( s ) ∀ s \pi^*=argmax_{\pi} \upsilon_\pi(s) \ \ \ \ \forall s π∗=argmaxπυπ(s) ∀s
或者说对于每一种状态对应的动作,我们希望其状态动作值函数最大化
a t ∗ = a r g m a x a i q π ∗ ( a i , s t ) a_t^*=argmax_{a_{i}}q_{\pi^*}(a_{i},s_t) at∗=argmaxaiqπ∗(ai,st)
那么如何求解这个策略呢?
策略迭代
1.从某种策略 π \pi π开始,计算当前策略下的值函数 V π ( s ) V_\pi(s) Vπ(s)
2.利用值函数寻找更好的策略 π ∗ \pi^* π∗
3.重复1直到策略收敛
计算值函数(利用BELLMAN EQUATION):
υ π ( s t ) = ∑ a t π ( a t ∣ s t ) ∑ s t + 1 p ( s t + 1 ∣ s t , a t ) [ r t + 1 + υ π ( s t + 1 ) ] \upsilon _\pi(s_{t}) = \sum_{a_t} \pi(a_t|s_t) \sum_{s_{t+1}}p(s_{t+1}|s_t,a_t) [r_{t+1} +\upsilon _\pi(s_{t+1})] υπ(st)=at∑π(at∣st)st+1∑p(st+1∣st,at)[rt+1+υπ(st+1)]
这个公式是一个时刻,对于所有时刻可表示为如下形状的矩阵运算
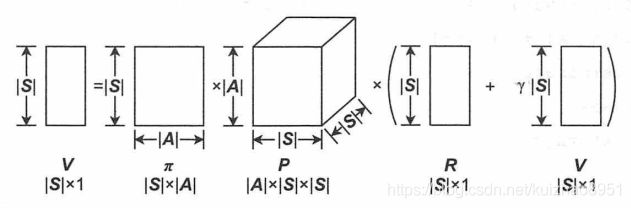 V = Π P ( R + γ V ) V=\Pi P(R+\gamma V) V=ΠP(R+γV)只要 ( 1 − γ Π P ) − 1 (1-\gamma \Pi P)^{-1} (1−γΠP)−1存在,可以求得解析解: V = ( 1 − γ Π P ) − 1 Π P R V=(1-\gamma \Pi P)^{-1}\Pi P R V=(1−γΠP)−1ΠPR
V = Π P ( R + γ V ) V=\Pi P(R+\gamma V) V=ΠP(R+γV)只要 ( 1 − γ Π P ) − 1 (1-\gamma \Pi P)^{-1} (1−γΠP)−1存在,可以求得解析解: V = ( 1 − γ Π P ) − 1 Π P R V=(1-\gamma \Pi P)^{-1}\Pi P R V=(1−γΠP)−1ΠPR
不过在状态空间或者行为空间大的时候采用迭代求解。
υ T ( s t ) = ∑ a t π ( a t ∣ s t ) ∑ s t + 1 p ( s t + 1 ∣ s t , a t ) [ r t + 1 + γ υ T − 1 ( s t + 1 ) ] \upsilon ^T(s_{t}) = \sum_{a_t} \pi(a_t|s_t) \sum_{s_{t+1}}p(s_{t+1}|s_t,a_t) [r_{t+1} +\gamma \upsilon ^{T-1}(s_{t+1})] υT(st)=at∑π(at∣st)st+1∑p(st+1∣st,at)[rt+1+γυT−1(st+1)]
若采用确定策略(就像上面的表格Agent),那么不必进行概率计算 π ( a t ∣ s t ) = 1 \pi(a_t|s_t)=1 π(at∣st)=1
策略迭代 代码
def policy_evaluation(self, agent, max_iter = -1):
iteration = 0
# iterative eval
while True:
# one iteration
iteration += 1
new_value_pi = agent.value_pi.copy()
for i in range(1, agent.s_len): # for each state 更新所有状态的值函数
#agent的action
ac = agent.pi[i]
#动作ac action; i 原来的状态 p(s'|s,a)
transition = agent.p[ac, i, :]
#此处因为是确定策略,所以pi=1
value_sa = np.dot(transition, agent.r + agent.gamma * agent.value_pi)
new_value_pi[i] = value_sa
#计算差值,足够小或者超过最大迭代次数的时候退出
diff = np.sqrt(np.sum(np.power(agent.value_pi - new_value_pi, 2)))
# print 'diff={}'.format(diff)
if diff < 1e-6:
break
else:
agent.value_pi = new_value_pi
if iteration == max_iter:
break
完成对此次状态值函数的更新之后,根据更新的状态值函数计算状态-行为值函数
q ( s t , a t ) = ∑ s t + 1 p ( s t + 1 ∣ s t , a t ) [ r t + γ υ ( s t + 1 ) ] q(s_t,a_t)=\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)[r_t+\gamma\upsilon(s_{t+1})] q(st,at)=st+1∑p(st+1∣st,at)[rt+γυ(st+1)]
最后,根据q完成策略的更新
π ( s ) = a r g m a x a q ( s , a ) \pi(s)=argmax_aq(s,a) π(s)=argmaxaq(s,a)
def policy_improvement(self, agent):
new_policy = np.zeros_like(agent.pi)
for i in range(1, agent.s_len):
for j in range(0, agent.a_len):#更新q
agent.value_q[i,j] = np.dot(agent.p[j,i,:], agent.r + agent.gamma * agent.value_pi)
# update policy
max_act = np.argmax(agent.value_q[i,:])
new_policy[i] = max_act
if np.all(np.equal(new_policy, agent.pi)):
return False
else:
agent.pi = new_policy
return True
最后将上面的代码联起来
def policy_iteration(self, agent):
iteration = 0
while True:
iteration += 1
self.policy_evaluation(agent)
ret = self.policy_improvement(agent)
if not ret:
break
print 'Iter {} rounds converge'.format(iteration)
效果测试
def policy_iteration_demo1():
env = SnakeEnv(0, [3,6])
agent = TableAgent(env)
pi_algo = PolicyIteration()
pi_algo.policy_iteration(agent)
print 'return_pi={}'.format(eval_game(env, agent))
print agent.pi
此处不证明策略提升的收敛性
价值迭代
如果对程序计时,会发现策略迭代算法大部分时间都花在策略评估(计算V)上,对于复杂的问题,策略评估有时候花费的实践会过于长,那么我们是否能放弃策略评估的一些精度,帮我加速算法呢?价值迭代会告诉你,其实的确没必要那么精确
我们通过对迭代次数的限制不断变小的实验发现,策略评估的迭代轮数降低,算法的总迭代数在升高,但是这一的改变并不会影响最终结果,反而成了实验中速度最快的算法——评估迭代轮数为1的策略评估算法。
 如上图右侧6-7所示,与其说这是更新策略,不如说是更新价值,当价值迭代完成之后,策略迭代也就随之完成。
如上图右侧6-7所示,与其说这是更新策略,不如说是更新价值,当价值迭代完成之后,策略迭代也就随之完成。
这里推荐读者去看书中对价值迭代的代码以及描述,代码上十分相同,只不过和策略迭代不同的是,策略迭代每一次是已经选出之前策略基于此次状态选择的最佳动作 π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st),然后去更新值函数到一定精度然后去更新q值再去更新策略,主要关注策略的更新,策略更新很多次;而价值迭代虽然也是首先更新值函数(V),但是是求出所有动作可能的值函数(通过BELLMAN EQUATION)然后选择使得值函数最大的action当作当时选择的动作,然后在到达一定精度之后,一次性更新策略,策略是根据完全收敛的值函数得到的。
两者的共同点
1.最终都求出策略函数和值函数
2.最优策略函数都是通过收敛的值函数得到的
3.值函数都通过BELLMAN EQUATION收敛
只是两个算法的侧重点不同,策略迭代的核心是策略,为了提升策略,求解的值函数可以精准,也可以没那么精准;而价值迭代的核心是价值,算法核心没有出现和策略相关的内容,直到最后值函数收敛后才求出策略
广义策略迭代法(结合)
广义的策略迭代法其实是迭代算法族,其中的算法都是由策略迭代和价值迭代组合而成的,组合方法很多,所以称广义。通过设计可以使得速度比这两个算法都快(如果涉及不当可能不会),书中只是简单先执行十轮价值迭代,然后进行策略迭代,同时策略迭代中的策略评估只进行一个循环的跟新,发现效果的确更好(速度更快)
由于书中并未做更多解释,此处也不赘述