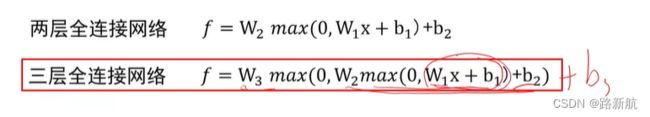计算机视觉与深度学习（线性分类器、全连接神经网络）

参考：https://www.bilibili.com/video/BV1V54y1B7K3

图像分类

1. 什么是图像分类任务，它有哪些应用场合?

2. 图像分类任务有哪些难点?
   视觉、光照、尺度、遮挡、形变、遮挡、形变、背景杂波、类内形变、运动模糊

3. 基于规则的方法是否可行?

4. 什么是数据驱动的图像分类范式?

5. 常用的分类任务评价指标是什么?

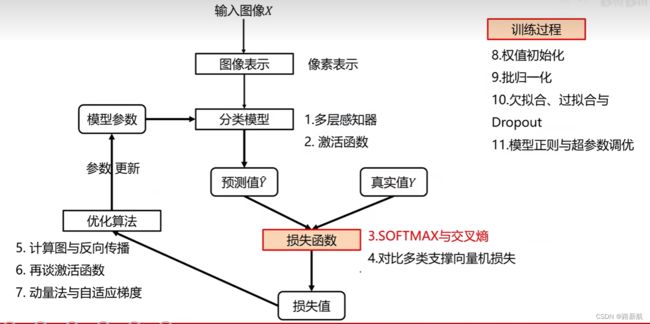
数据驱动的图像分类方法

1.数据集构建

有监督、无监督数据

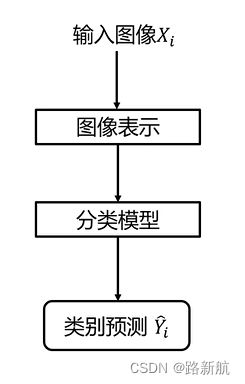
2.分类器设计与学习

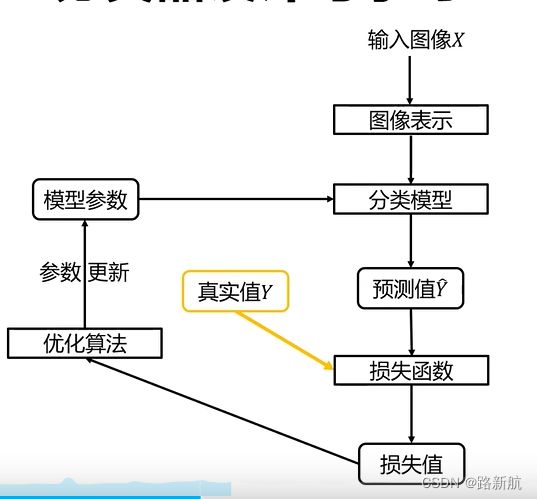
图像表示：
像素表示
全局特征表示（如GIST，抽出频率，适合城市建筑、风景、大场景分类）
局部特征表示（如SIFT特征+词袋模型）

3.分类器决策

分类器

• 近邻分类器
• 贝叶斯分类器
• 线性分类器
• 支撑向量机分类器
• 神经网络分类器
• 随机森林
• Adaboost

了解每个工具的优势和劣势，
懂原理：工具需要修改，以适应场景

损失函数

• 0-1损失
• 多类支撑向量机损失
• 交叉嫡损失
• L1损失
• L2损失

优化方法

一阶方法

• 梯度下降
• 随机梯度下降
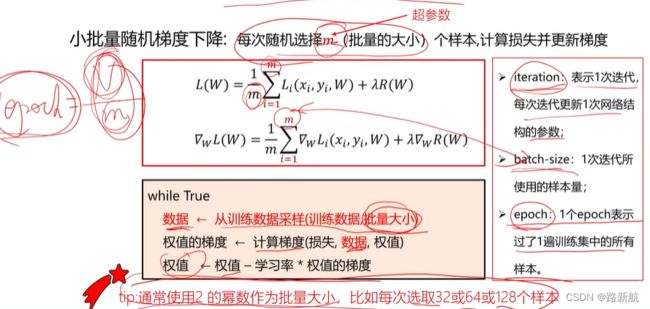
• 小批量随机梯度下降

二阶方法

• 牛顿法
• BFGS
• L-BFGS

训练过程

• 数据集划分
• 数据预处理
• 数据增强
• 欠拟合与过拟合
  • 减小算法复杂度
  • 使用权重正则项
  • 使用dropout正则化
• 超参数调整
• 模型集成

评价指标

正确率
错误率
top1、top5正确率

线性分类器

数据集：CIFAR10数据集

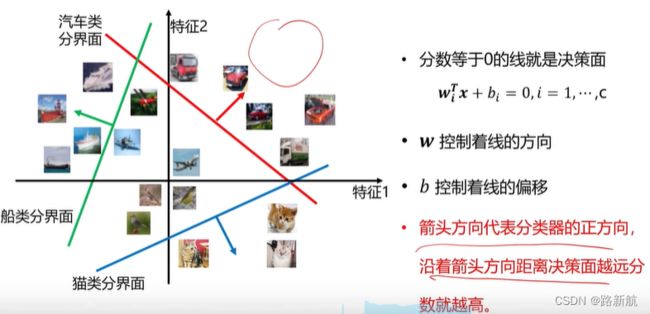
定义

线性分类器是一种线性映射，将输入的图像特征映射为类别分数。

线性分类器决策步骤

1. 图像表示成向量
2. 计算当前图片每个类别的分数
3. 按类别得分判定当前图像

统计：模板记录了统计信息

几何：分界面

损失函数

定义：用于度量分类器预测值和真实值不一致成都，输出的非负实值可以作为反馈信号来对分类器参数进行调整，以降低当前示例对应的损失值，提升分类器分类效果

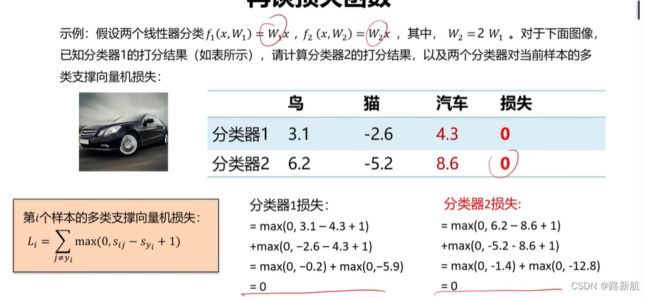
多类支持向量机损失

例子

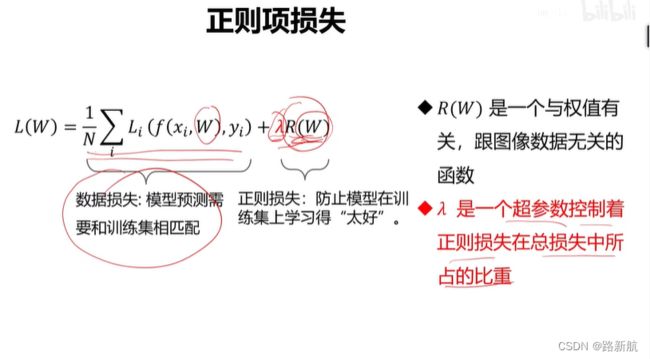
正则项

解决唯一性，让模型有了偏好，

超参数：在开始学习过程之前设置，对模型性能有着重要的影响。

L2正则项

常用的正则项损失

参数优化

定义：机器学习核心步骤之一，利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能

优化算法目标

梯度下降算法

方向：负梯度方向
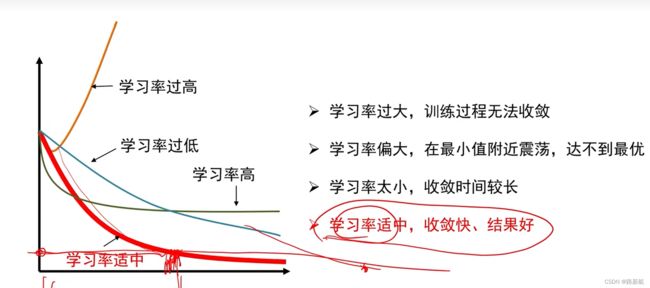
走多远：步长，学习率

梯度向量
1.数值法，计算量大，不精确！

2.解析法，精确 速度快 函数导数推导容易错

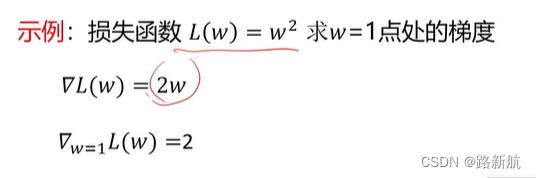
数值梯度有什么作用?
答:求梯度时一般使用解析梯度，而数值梯度主要用于解析梯度的正确性校验（梯度检查)。

梯度下降算法的计算效率

速度太慢

随机梯度下降算法

每次迭代朝着整体最优梯度方向

小批量梯度下降算法

总结

数据集划分

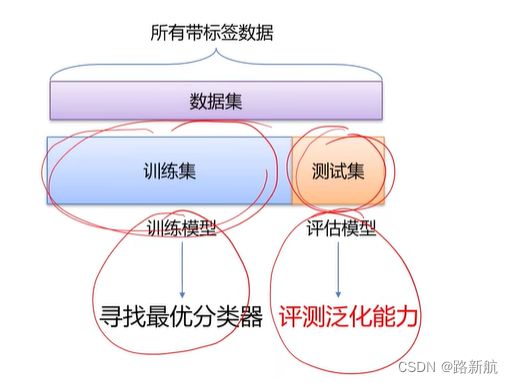
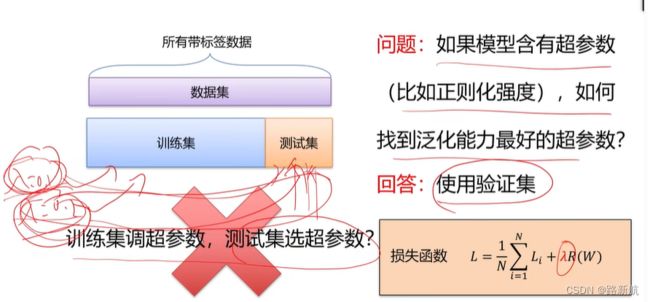
测试集 上计算精度

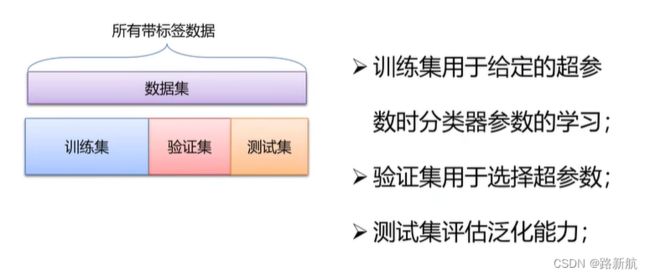
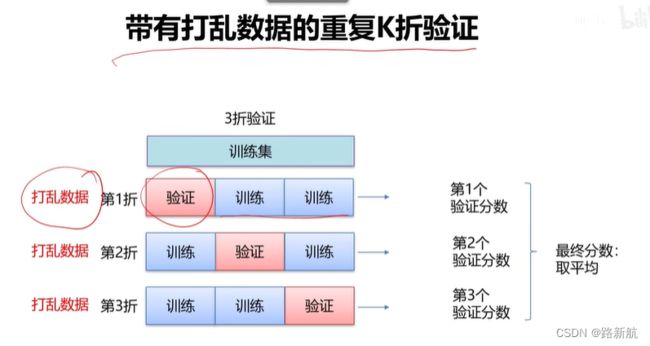
K折交叉验证
数据太少，验证集合包含的样本太少，如果再划分数据钱进行不同的随机打乱，最终得到的模型性能差别很大。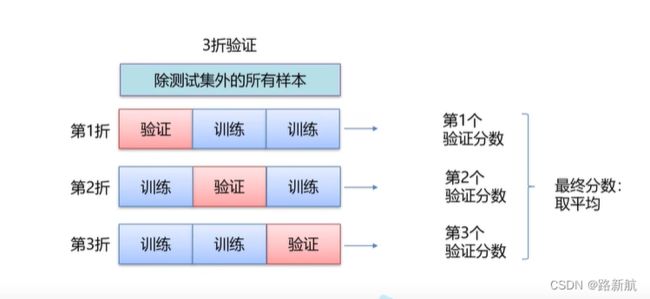

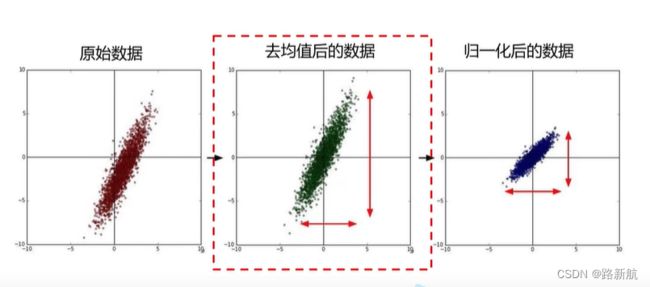
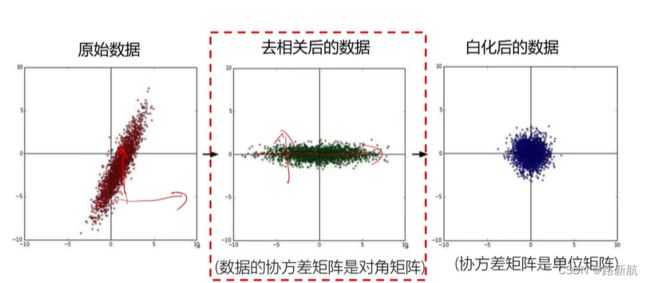
通常取5折、10折

数据预处理

去均值：数值都在中心，反映相对差值，，不会受到数值范围影响
归一化：让两个方向不会受到数值范围影响，去量纲影响

去相关
让数据独立、不考虑一些维度，达到降为维度效果

全连接神经网络

全连接神经网络级联多个变换来实现输入到输出的映射。
/多个线性分类器通过级联后的结果

注意非线性操作不可以去掉

多层感知器

全连接神经网络的权值

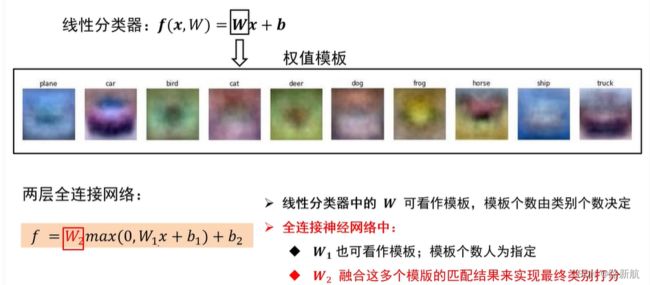
通过指定模板个数，使得模板更准确，模板越多，记录的信息越准确
（全联接神经网络的描述能力更强。因为调整W行数等于增加模板个数,分类器有机会学到两个不同方向的马的模板）

全连接神经网络与线性不区别

全连接神经网络与线性分类器区别：
线性分类器只能解决线性可分的问题
全连接神经网络可以解决线性不可分的问题

依赖全连接网络非线性操作，通过非线性映射关系， 实现线性不可分的类别的学习

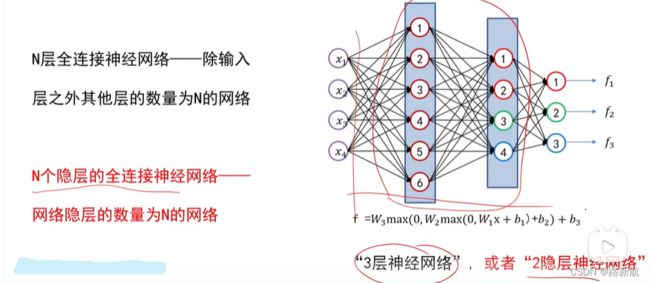
全连接神经网络绘制与命名

通常选择第二种表示

N层神经网络
N=除了输入层的其他层数

激活函数

多层感知器最关键的是激活函数

去掉激活函数，全连接神经网络退化成线性分类器
常用激活函数:
sigmoid 不是对称的，5的时候接近于1，映射到(0,1)
tanh 对称，3的时候接近于1，映射到(-1,1)
ReLU，比0大就是自己，小于0等于0
Leaky ReLU=max(0.1x,x)

网络结构设计

神经元个数越多，分界面可以越复杂，在这几个集合上的分类能力越强

1.用不用隐层，用一个还是用几个隐层?(深度设计)
2.每隐层设置多少个神经元比较合适?(宽度设计)
没有统一的答案!

依据分类任务的难易程度来调整神经网络模型的复杂程度。分类任务越难，我们设计的神经网络结构就应该越深、越宽。但是，需要注意的是对训练集分类精度最高的全连接神经网络模型，在真实场景下识别性能未必是最好的(过拟合)。

小结

• 全连接神经网络组成:一个输入层、一个输出层及多个隐层;
• 输入层与输出层的神经元个数由任务决定，而隐层数量以及每个
  隐层的神经元个数需要人为指定;
• 激活函数是全连接神经网络中的一个重要部分，缺少了激活函数，
  全连接神经网络将退化为线性分类器。

损失函数

SOFTMAX

(logistic回归扩展)
把神经网络的绝对输出变成概率

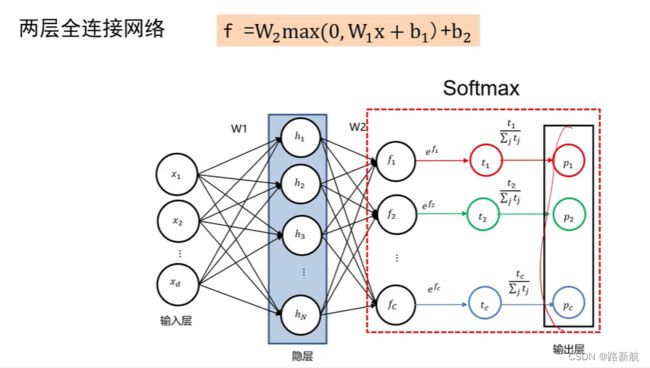
示例

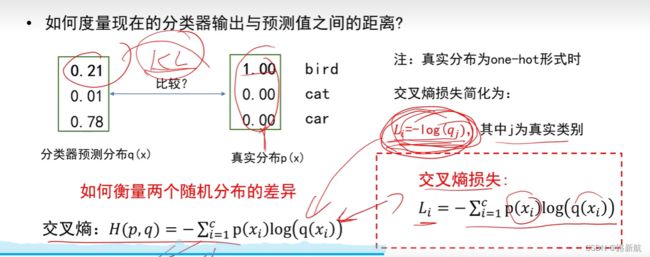
交叉熵

定义：度量两个分布的距离，两个分布越接近，交叉熵损失值越小

预测分布于one-hot表示的真实分布

多类支撑向量机损失，只考虑xi是否大于xj大过1，希望两个分布越接近越好

熵，反映信息量的大小
[1,0,0] H§最小，[1/3,1/3,1/3]H§最大

之所以叫散度，而不是距离，距离有交换性。

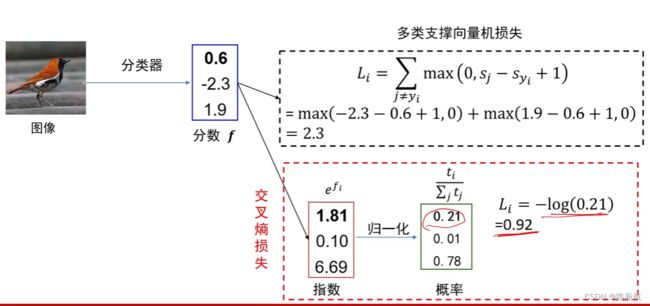
交叉熵损失vs多类支撑向量机损失

计算过程比较：

计算结果：
一个类别概率高的时候，压低别的类别概率方向优化

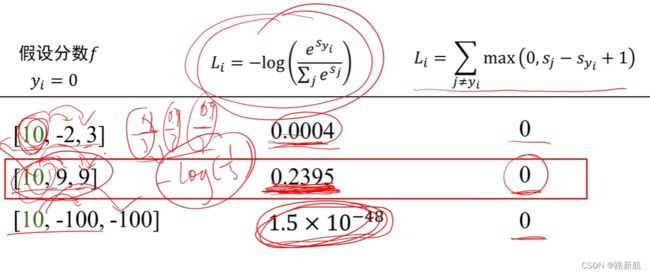
损失可能变化很小，预测精度上升

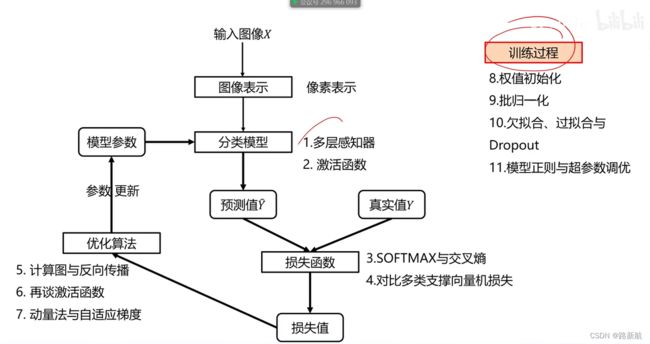
优化算法

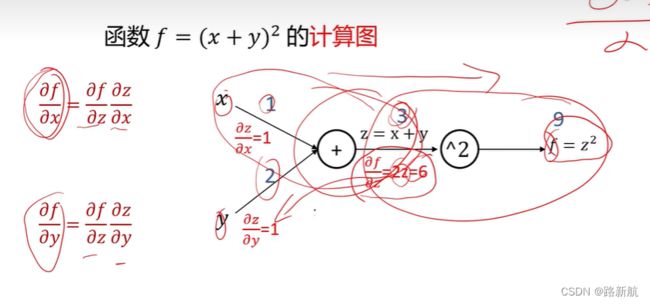
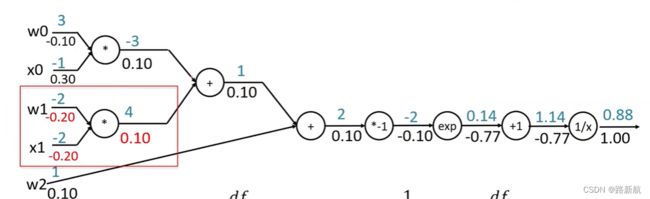
计算图与反向传播

计算图帮助计算输出相对于任何w的梯度

计算图是一种有向图，它用来表达输入、输出以及中间变量之间的计算关系，图中的每个节点对应着一种数学运算。

正向：可以求结果
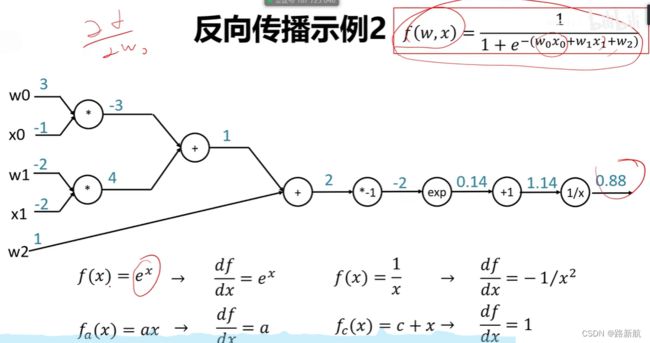
反向：使用链式法则，可以算输出到输入梯度

f 对 f求导就是1

总结
任意复杂的函数，都可以用计算图的形式表示
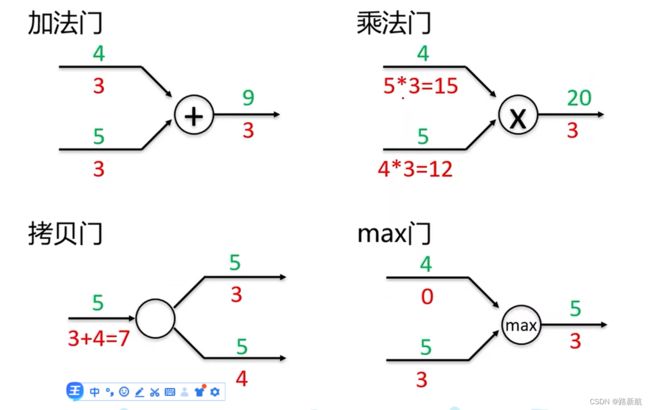
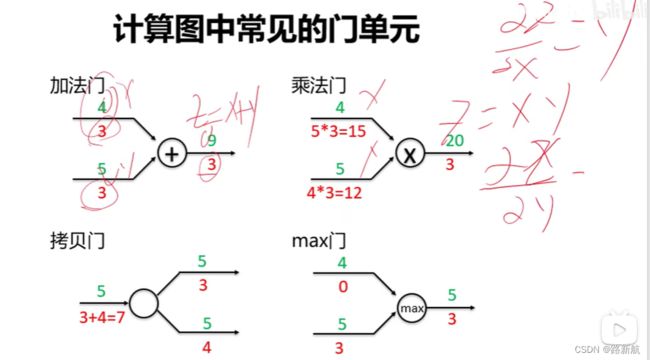
在整个计算图中，每个门单元都会得到一些输入，然后，进行下面两个计算:
a)这个门的输出值
b)其输出值关于输入值的局部梯度。

利用链式法则，门单元应该将回传的梯度乘以它对其的输入的局部梯度，
从而得到整个网络的输出对该门单元的每个输入值的梯度。

计算图颗粒度
caffe 写出一些函数，把导数求出来，写入到计算模块，提高效率
tensorflow 所有算法拆解成计算图，计算效率比较低

计算图常用的门单元

再谈激活函数

梯度消失，梯度消失 本质是由于链式法则的乘法特性导致的。

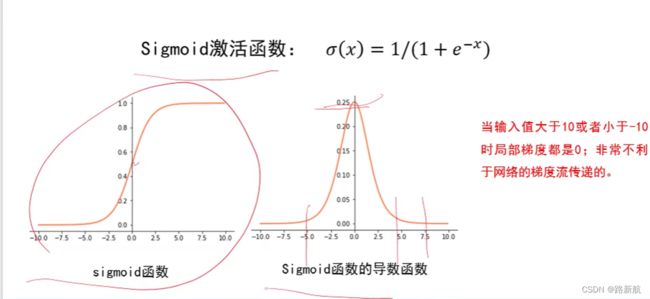
sigmoid激活函数，求导后最大为1/4，很多时候为0，梯度回传容易消失

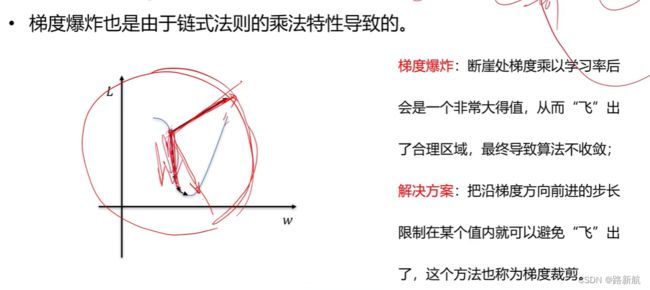
梯度爆炸
梯度爆炸也是由于链式法则的乘法特性导致的。

导致步长太长，可以做梯度裁剪

tanh(x)

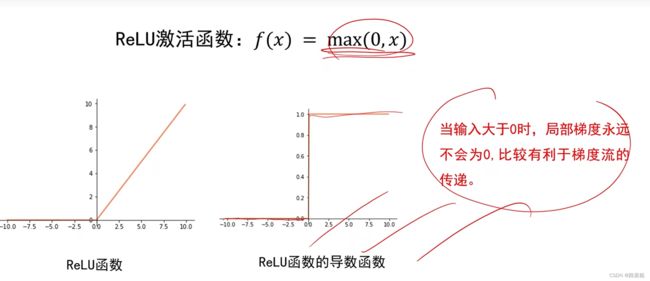
relu函数，计算简单

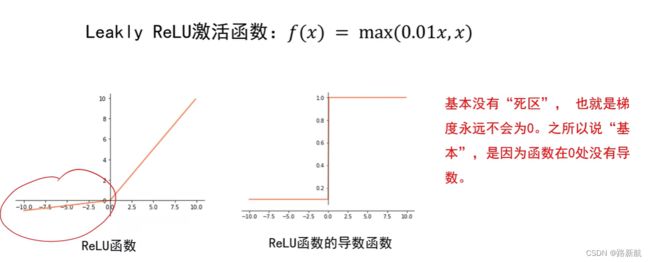
Leakly Relu，0没有导数（但基本不会出现0）

尽量选择ReLU函数或者Leakly ReLU涵数，相对于Sigmoid/tanh,
ReLU函数或者Leakly ReLU函数会让梯度流更加顺畅,训练过程收敛得更快。

动量法与自适应梯度

梯度算法改进

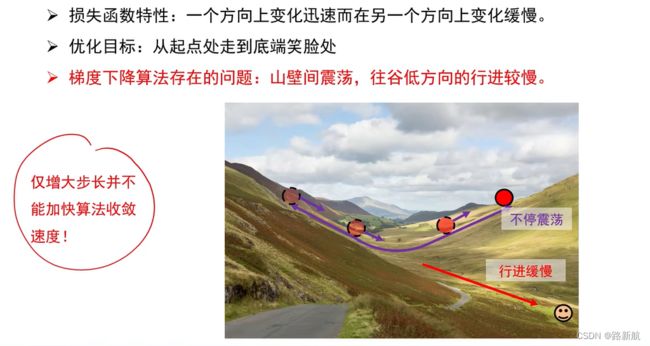
• 梯度下降算法存在问题
• 动量法
• 自适应梯度与RMSProp
• ADAM
• 总结

梯度下降算法存在问题

动量法

目标：改进梯度下降算法存在的问题，即减少震荡
改进思想：利用累加历史梯度信息更新梯度

v是累加值


不为1会慢慢衰减，

累加值 累加过程中 震荡梯度会被减弱，走的很慢但是一致的方向会被加强

动量法还有什么效果？
避免鞍点

自适应梯度与RMSProp

自适应梯度法

AdaGrad

累加过程此消彼长
作用：参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

缺点：由于是累积平方梯度，导致学习率过快接近0

r累加过大，调节梯度能力变弱

RMSProp

ADAM

总结
常用：SGD+动量（效果很好，需要调参） ，ADAM

动量（不动再往下降）

训练过程

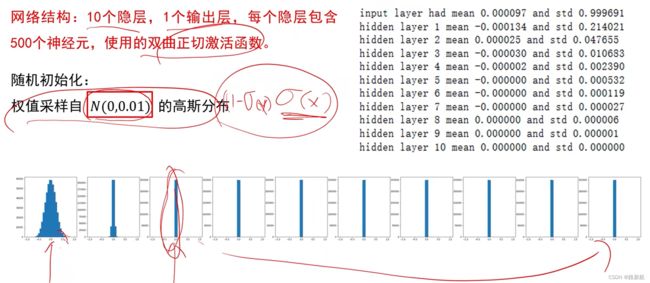
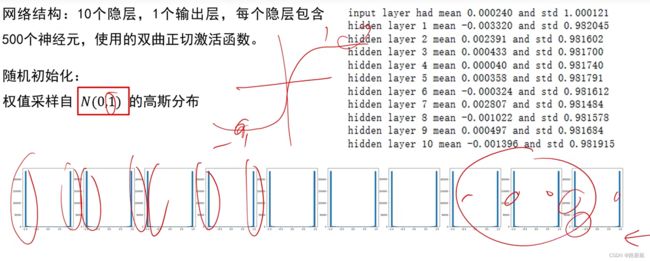
权值初始化

建议：采用随机初始化

参数都一样，无法训练

初始化不好，网络无法训练
输出为0，衰减，无法训练

实验结论：
初始化时让权值不相等，并不能保证网络能够正常的被训练。
有效的初始化方法：使网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致，以保持网络中正向和反向数据流动。

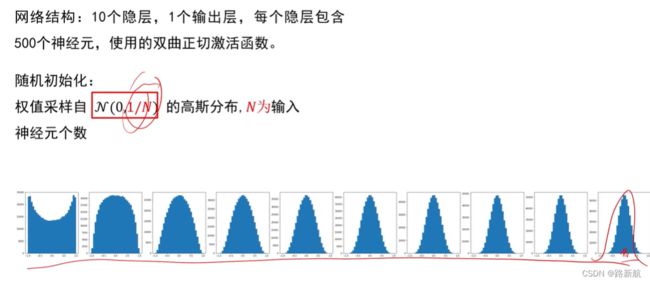
Xavier初始

tanh


输入与输出有相同的分布

ReLU
多次迭代后输出大部分集中在0

HE初始化（MSRA）

总结

• 好的初始化方法可以防止前向传播过程中的信息消失，也可以解决反向传递过程中的梯度消失。
• 激活函数选择双曲正切或者Sigmoid时，建议使用Xaizer初始
  化方法;
• 激活函数选择ReLU或Leakly ReLU时，推荐使用He初始化方法。

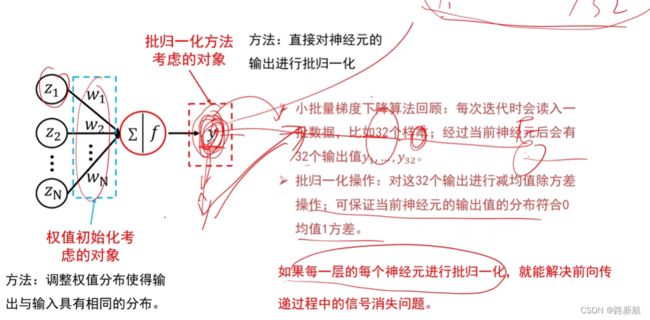
批归一化

输出 批归一化，解决梯度消失，放在非线性操作前

• 正向传播，不至于无信息
• 反向传递，梯度在最有效范围内

gama（分布的方差）和beta（分布的中心）自己学习（）

问题:单张样本测试时，均值和方差怎么设置?
回答:来自于训练中。累加训练时每个批次的均值和方差，最后进行平均，用平均后的结果作为测时的均值和方差。

加入批归一化，让神经网络初始值不那么敏感

欠拟合、过拟合与dropout

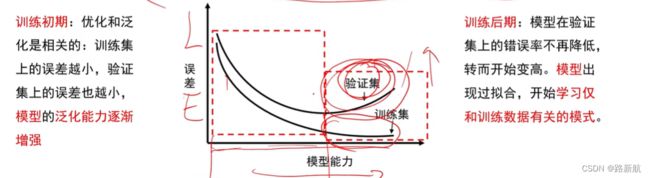
过拟合：
定义：深度学习常常遇见的现象，出现过拟合，得到的模型在训练集上的准确率很高，但在真实的场景中识别率确很低。

过拟合——是指学习时选择的模型所包含的参数过多，以至于出现这一模型对已知数据预测的很好，但对未知数据预测得很差的现象。这种情况下模型可能只是记住了训练集数据，而不是学习到了数据特征

欠拟合——模型描述能力太弱，以至于不能很好地学习到数据中的规律。产生欠拟合的原因通常是模型过于简单

• 机器学习的根本问题是优化和泛化的问题。
• 优化——是指调节模型以在训练数据上得到最佳性能;
• 泛化——是指训练好的模型在前所未见的数据上的性能好坏。
  

应对过拟合
最优方案：获取更多的训练数据
次优方案：

分散权值

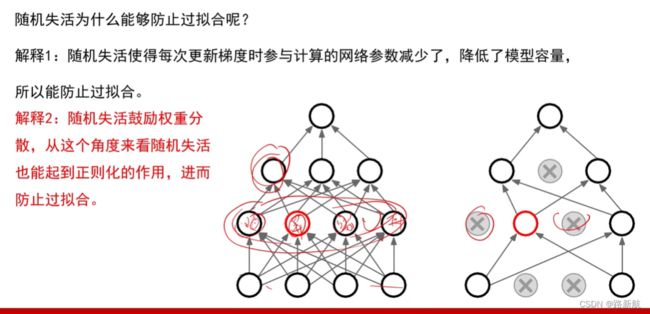
随机失活 Dropout

模型参数减少
权重分散，起正则化

信息不过于集中，也让每个神经元记录更多信息

多个小网络集成

训练阶段与测试阶段不一致，测试阶段需要乘以P

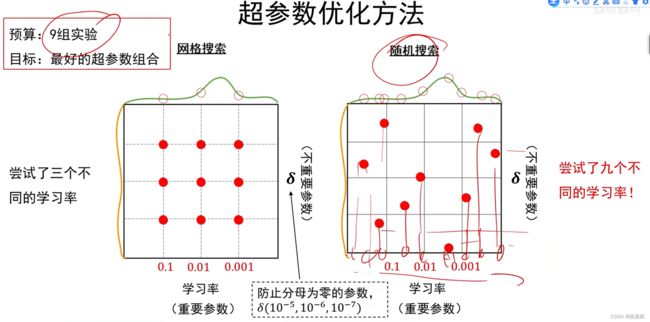
模型正则与调参优化

超参数优化方法
网格搜索法：
随机搜索法：

超参数搜索策略