技术内幕 | StarRocks Community Champion、阿里云技术专家解读 Optimizer 实现
**作者:范振(花名辰繁),阿里云计算平台-开源大数据-OLAP方向负责人,高级技术专家,StarRocks Community Champion**
随着阿里云EMR StarRocks 上线,在和用户交流的过程中,越来越多被问到 StarRocks 和 ClickHouse 的区别,其中 Join 能力最受客户关心。提到 Join,最为重要的便是 Optimizer 的实现,所以我来写一篇关于 Optimizer 的详解文章,希望给大家一个全面的理解。
StarRocks 作为近年来非常优秀的 OLAP 引擎,在 Planner/Optimizer 上有高效、稳定的实现,这篇文章会从分析主流 Optimizer 框架的模型入手,详细解构 StarRocks 的 Optimizer 实现过程。
内容提要:
- Cascades/Orca 论文涉及的 Top-Down 优化思路与分析。
- 针对 CMU15-721 的一些 PPT、观点、结论加以解析。
- 着重结合 StarRocks 的实现,并介绍 StarRocks 的 Optimizer 主要借鉴的 CMU noisepage(https://github.com/cmu-db/noisepage) 项目以及 Cascades/Orca 论文的思路。
**#01**
**SQL 优化流程图**
**—**
在业务上,我们遇到了以下几个主要痛点:
下图体现了 SQL 文本到最终的分布式 Physical Plan 的全流程:
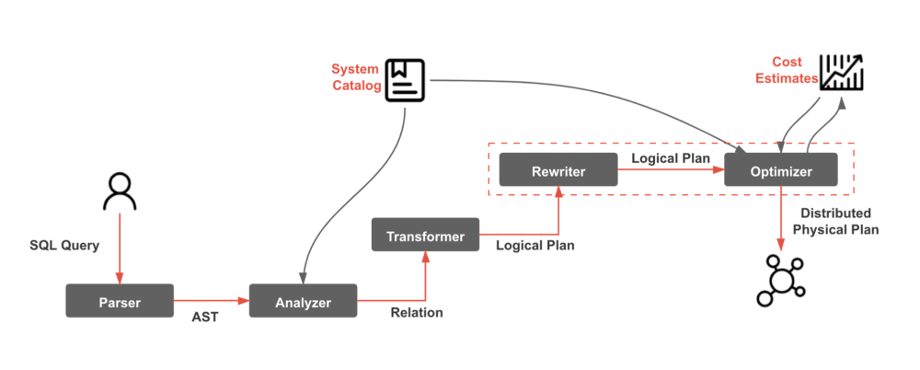
- Analyzer 需要结合内部/外部 Catalog 系统,主要是检查 Table、Column 等信息是否合法。
- Rewriter 阶段(RBO)主要是一些 Logical->Logical 的变换操作,基于一些经典的代数变换来进行。
- Optimizer(CBO)需要结合内部/外部的 Cost 模块,常用的计算采集信息包括行数、列基数、列最大最小值、每行平均大小、直方图等信息。
本文主要聚焦在 CBO 阶段的技术原理解析。
**#02**
**Rewriter**
**—**
Tree Rewrite 的过程大体思路是:
- 本质上是二叉树的转换,利用已知的 Transformation Rule 和已知的 Pattern,对逻辑二叉树做匹配、转换,形成一棵新的二叉树。
- Top-Down 的迭代(即每条 Rule 自顶向下的匹配 Tree 以及 Subtree)方式,将所有符合规则的 Rule全部应用到逻辑二叉树,形成新的逻辑二叉树。
我们以下图的 Predicate PushDown 为例进行分析:
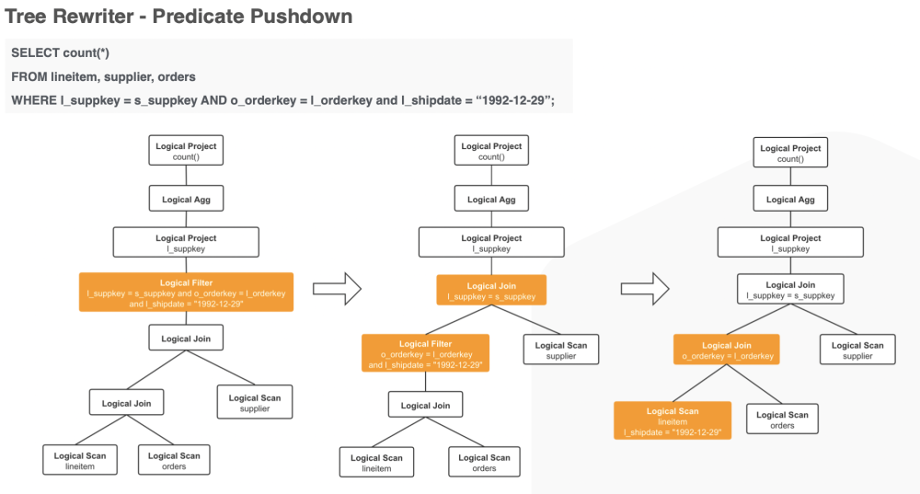
每一个 Transformation Rule 有一个 Pattern,首先会检查 Rule 的 Pattern 是否能够 Match Logical Tree,本例中以下的 Rule 可以匹配上图的 Tree。

- 确认能够匹配之后,就是 Tree 的 Transform 过程,针对本例大体流程是:
- 将 FilterOperator 的 Predicates 分裂开,可以得到几个 Predicates。
- 根据 Pattern 的数据结构可知,取 FilterOperator 的子节点,一定是 JoinOperator 。将匹配的 Predicates 分给 FilterOperator,将不匹配的 Predicates 生成新的 FilterOperator 挂到FilterOperator 的 2 个子节点之上、JoinOperator 之下。
- 这样就完成了一层下推动作,同理继续迭代的进行 Subtree 的匹配、下推操作。
当所有的 Rules 都进行了一次匹配操作之后(如果 Match 不匹配,不进行 Transform),Rewriter 的工作就结束了,得到了一个新的 Logical Plan。
**#03**
**CBO 架构**
**—**
**1、** 整体优化思路
CBO 的目标是将一棵重写后的 Logical Tree 转换为 Physical Tree,使得这棵 Physical Tree 的执行代价最小,或者是在一定约束下的“最小”(这里的条件实质指的是 Property,每个 Property 对应一个最小代价的 Tree,或者说 Plan)。
查询优化的整体思路是:
- 通过逻辑变换(代数变换),找到所有等价的 Logical Plan,例如 Join 的交换律、结合律等。
- 将 Logical Plan 转变成 Physical Plan,例如将 LogicalJoin 拓展为 PhysicalHashJoin、PhysicalSortMergeJoin、PhysicalNestLoopJoin 等,将 LogicalScan 拓展为 SeqScan、IndexScan等。
- 第一步、第二步确立了完整的、统一的搜索空间。
- 根据不同算子的代价模型,计算出每一种 Physical Plan 的代价。
- 选取代价最小的作为最终的 Physical Plan。
但是,面临着几个问题:
- 根据逻辑计划推导出的物理计划特别多,多表 Join 膨胀的数量级比较大,在有限时间内可能无法全部计算。
- 要知道哪些 Subtree 的代价被计算过了,要知道哪些 Transformation Rule 针对哪些算子被应用过了。
- 需要尽量通过减少搜索空间,尽早地剪枝。
- 如何评估每个算子的代价。
查询优化的几个比较重要的原则,参考《CMU15-721-Optimizer》中所述:
- 对于一个给定的查询,找到一个正确的,最低“cost”的执行计划
- 这是数据库系统中最难实现好的一部分(是一个 NP 完全问题)
- 没有优化器能够真正产生一个“最优的”计划,我们总是
- 用估算的方式去“猜”真实计划的 cost
- 用启发式(heuristics)的方式去限制搜索空间的大小
早期关于 CBO 、特别是 Bottom-Up 系列的优化器,应用很少,忽略不讲。关于现代优化器的一些Paper 的研究情况大致如下:
- Volcano 是更早的 Top-Down 优化框架,现代数据库已经没有落地,忽略不讲。
- Cascades 是改进 Volcano 的另一种基于 Top-Down 的优化框架,是现代数据库应用的最多的 Optimizer 框架,论文比较抽象,指出了很多方法论,实践意义比较强。
- ORCA 是针对大数据场景的、基于 DXL 通信的 Standalone 的优化器(可以把优化器部分抽出来,独立 service 部署),它引入了 Distribution(包括 Shuffle、Broadcast 等网络传输算子)的Property,规范了可能的数据分布。ORCA 可以认为是 Cascades 的优化实现版本,给出了更加丰富的实现细节和步骤。
**2、** Cascades Framework & ORCA Architecture\
**基础概念**
- Expressions

- Groups

- Rules

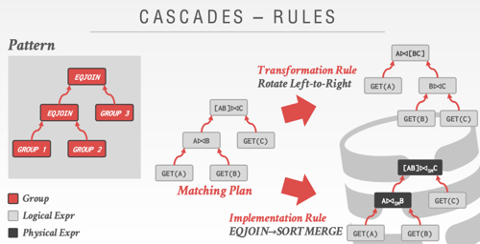
- Memo

**核心优化流程**
- Exploration,将原始的 Logical Plan 转成等价的 Logical Plan,比如 Join 的结合律、交换律等。
- Statistics Derivation,将所有的逻辑计划,沿着 Tree->Subtree Top-Down 方式进行统计信息搜集。实现中,可以认为是 Tree 的后根遍历,先进行子节点的 Statistics 搜集,再根据子节点提供的 Statistics 搜集自身的 Statistics。
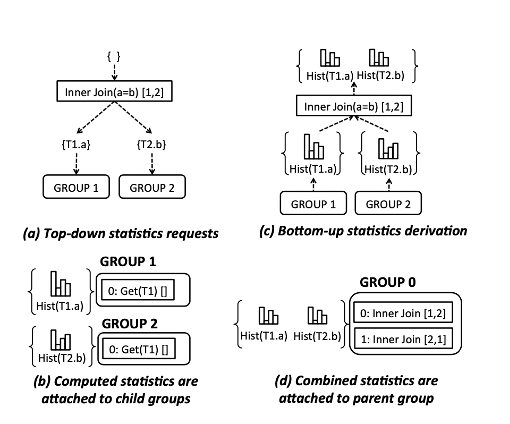
- Implementation,将所有 Exploration 得到的 Logical Plan 转成对应的 Physical Plan,转换过程中一个 Logical Plan 对应着多个 PhysicalPlan,比如 LogicalJoin,可以转换为 PhysicalHashJoin、PhysicalSortMergeJoin、PhysicalNLJoin等。
- Optimization,开始进行真正的计算代价,这部分会在后面的“优化的流程”章节中详细说明。
需要注意的是:真正实现过程中,不应该顺序按照这四步来,至少 StarRocks 不是这么做的。CMU15-721 以及 Cascades 论文都有解释:
- Stratified search vs unified search,分层搜索是先 Logical->Logical,再 Logical->Physical;统一搜索是 Logical->Logical 以及 Logical->Physical 一起都做了,都属于同一个 Group 中的等价变换。
- 这样做的好处是,在 Exploration Logical Plan 时,有可能其 Subtree 对应的 Physical plan 已经不满足条件(比如由于 Cost 过大,被剪枝了),所以不需要继续进行。Cascades 中与此思想接近的描述是:Cascades 搜索引擎确保只有那些真正可以参与查询评估计划的子树和相关联的(interesting)属性得到优化。每次当一个输入被优化之后,优化任务可以获得一个最小的 Cost,用这个 Cost 去限制下一次的优化输入上限。这样,可以尽可能地紧凑(tight)剪枝。
- 对于一个 Tree 或者 Subtree,它的 Cost 是逐渐递减的。会将上一次 Tree 计算得到的 Cost 结果当做下一次 Tree 的 Limit,这样有利于搜索剪枝,即一旦 Subtree 计算 Cost 的过程中超过 Limit,会立即被剪枝。
- 这样做需要更多的 Memo 存储空间。
**Property Enforcement**
在 ORCA 框架中 Property 有多种,这里重点介绍 Sort 和 Distribution,我们用{Sort,Distribution}表示,如果均为任意属性,表示为{Any, Any}。Property 实际上就是最终某个算子需要什么样的特性(Required Properties),举以下例子:
- Select a from A order by a。这个 Query 希望最终能够能够按照 Column a 来排序,那么我们会在查询最后加入对于 a 的排序特性来满足最终的需求,那么对于这个 Query 要求{Sort(A.a), Any}。同时父节点需要把 Required Property 传导下去,给到 Scan A 子节点。这样我们面临着两种选择:
- 要求子节点 Scan A 排序,即{Sort(A.a), Any},父节点 Project 不需要排序直接输出。
- 要求子节点不排序,即{Any, Any},父节点加入排序算子(即需要Enforce操作)后直接输出。
- 以上两种策略供我们选择,我们可以潜在利用 A 表的有序性,进行 IndexScan(例如利用 B+Tree 的有序性)。
- Select * from A Join B where A.a=B.b。这个 Query 中,我们对于Join结果没有分布要求, Property 可以为 Any。针对 PhysicalHashJoin 算子,我们有两组 Required Properties
- 左表A 是{Any, Any},右表B是{Any, Broadcast}。
- 左表A是{Any, Hash
为了满足 Required Properties,我们需要针对物理算子的实际行为,进行 Enforcer。比如 A 表并没有按照 Hash
加入了对应的 Enforcers,由于引入了新的算子(例如 Shuffle、Broadcast),我们计算 Cost,需要评估 Enforcers 本身的 Cost。
**优化的流程**
在分布式系统中,每一个 Group 对应的 Best Plan 实际上都是针对某一 Property 来说的,在 StarRocks 中是如下数据结构
- Map
- Map
所以 Optimizer 的工作就是不断根据 Rules Transformation 拓展得到 Logical/Physical Plan,插入到 Memo 中,通过比较 Cost 来不断迭代更新这两个数据结构。在搜索的过程中通过 Cost 来提早的 Prune 无效的 Subtree。
下图为 ORCA 最终的静态图,起始的 Required Property 为{Singleton,
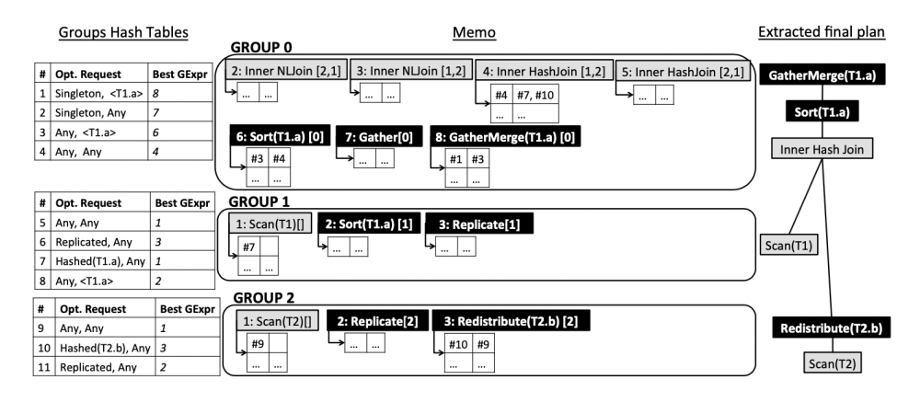
**动态规划算法解释**
- 整体的搜索过程是 DP 算法,最小 Cost 是问题(即DP[property_a,n])的最优解,它是所有 Exploration 得到的 Physical Plan 的解空间(即DP[property_b, n-1],DP[property_c,n-1] ...)中,满足特定 Property 的最小 Cost 值。这样问题就可以变成求子树的最小 Cost,就可以归为 DP 问题。
- 利用 Memo 来做 DP Memorization,每一个 Group 记录某一 Required Property 对应的 Best Expr。
- 通过 Cost Limit 的不断递减来做剪枝操作。
**#04**
**StarRocks 优化器详细解析**
**—**
**1、基础数据解构**
- 在 StarRocks 每一个 Logical Plan 中,Physical Plan 都可以认为是 OptExpression,下文我们称为 Logical Expression 和 Physical Expression。其中的 GroupExpression 和 OptExpression 可以互相经过变换生成。
- 起初的 Root OptExpression(经过 rewriter 后的 Logical Plan)经过封装形成 Root GroupExpression 后,后续基本所有的操作都是基于 GroupExpression 数据结构的。
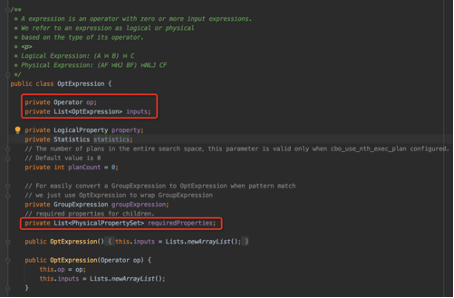
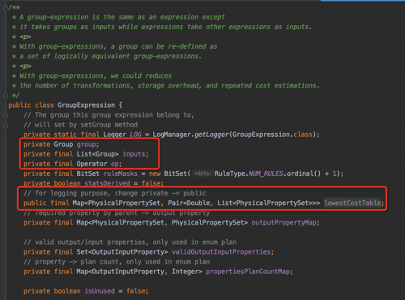
- StarRocks 基本遵循了 Cascades/ORCA 的思想,进行了一部分的改进,这些优化在上文中也有过描述,不再赘述,整体的架构如下。
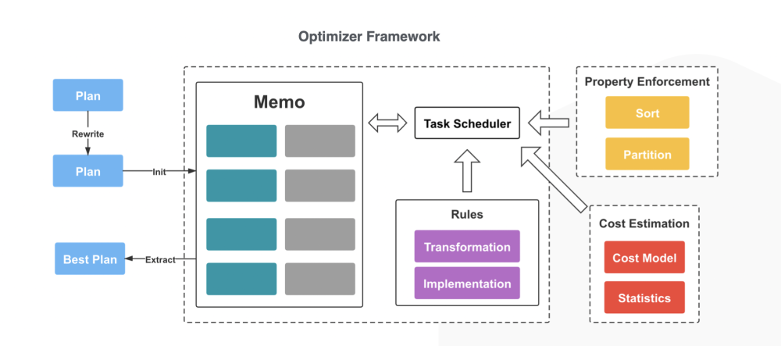
- StarRocks 中的 TaskScheduler 基于 Stack 和 OptimizerTask 抽象,实现了一套任务调度框架,Task 的类型有以下几种:
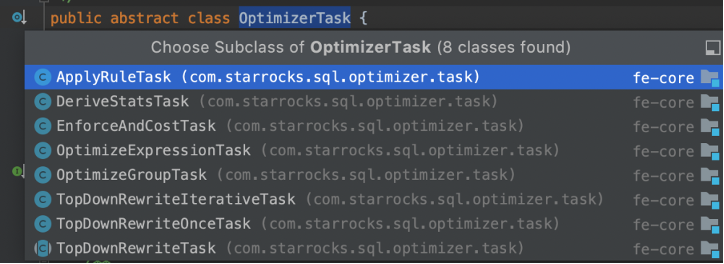
- DeriveStatsTask 对应 ORCA 中的 Statistics Derivation 过程,通过树的后根遍历来获得所有节点的 Statistics,注意这里的 Statistics 不是 Cost,通过 Logical Plan(主要是根据表、列的元信息统计)就可以获得每个 Group 对应的 Statistics。
- OptimizeExpressionTask 对应 ORCA 中的 Exploration 和 Implementation 过程。针对所有的 Rules(当前有 26 个 Implementation Rule 和 6+ 个 Transformation Rule)进行 Pattern 匹配,能够匹配 GroupExpression 对象的成为 Valid Rule,形成 ApplyRuleTask 对象。
- ApplyRuleTask 对应 ORCA 中的 Exploration 和 Implementation 过程。将 Rule 应用到 Logical Plan 中,实现 Logical->Logical、Logical->Physical 的转换,通过等价变换拓展每个 Group 的搜索空间。
- EnforceAndCostTask 对应了计算 Physical Plan 的 Cost 的过程,如果某个 Expression 不满足 Property,会 Enforce 出其他 Operator,例如 Broadcast、Shuffle、Sort 等算子。
**2、三表 Join 优化示例**
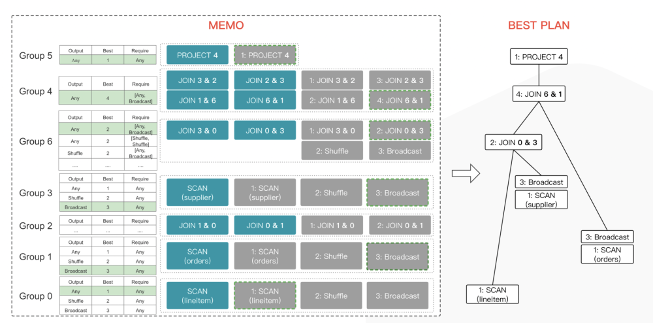
下面几张图以三表 Join 为例,体现了 StarRocks 的 Memo 不断变化的过程,最终通过上文中提到的 2 个数据结构的不断更新,得到了最终的 Best Plan。
- Memo Init 的过程,直接把三表 Join Rewriter 之后的 Logical Plan 插入到 Memo 中,得到了 6 个 Group。
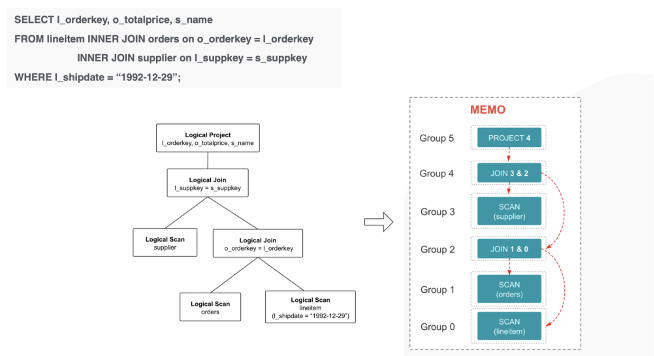
- 通过 Implementation Rule 对每个 Group 通过 Top-Down 遍历(利用 Stack 完成树的后根遍历)进行 Logical->Physical、Logical->Logical 的拓展。下图为 Join 交换律,由于 Join 交换律并没有增加新的 Join 组合,所以并没有新增 Group。
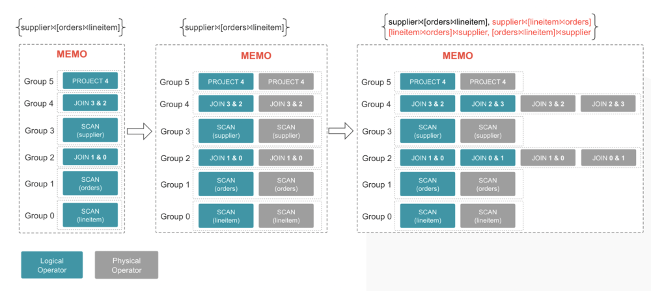
- 同样地,通过 Top-Down 遍历利用 Join 结合律进行 Transformation,由于 Join 结合律生成了新的 Join 组合,所以会新增 Group。
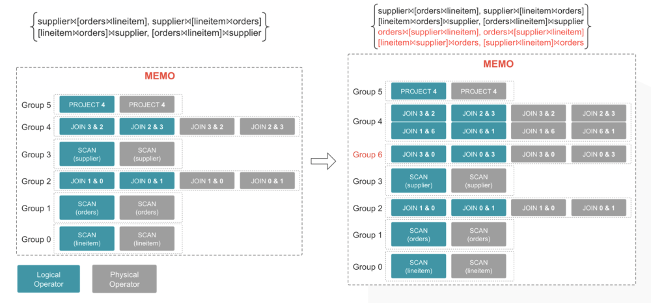
- 不断进行 Cost 计算,通过设置 Cost Limit 收敛进行剪枝,通过 Memo/Group 来记录每种不同的 Required Property 对应的 Best Expr,来更新上文提到的 2 个数据结构,最终到 Best Plan。
**3、CostModel**
StarRocks 中每个 Group 的 Statistics 有以下变量
- double outputRowCount
- Map
其中每个 Column 对应一个 ColumnStatistic 对象,主要有以下变量
- minValue
- maxValue
- averageRowSize
- distinctValuesCount
- ...
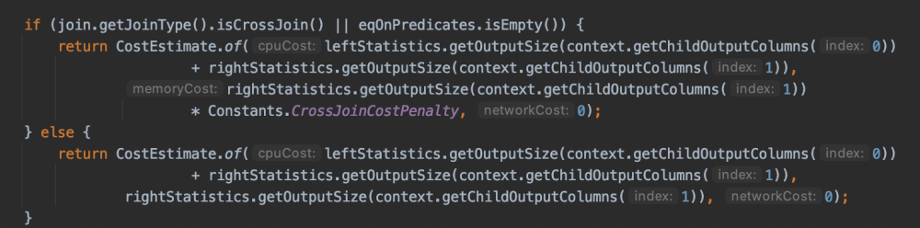
有了这些 Stats,我们其实可以预估任意一个算子的 Cost,比如预估 HashJoin 的方法如下图,即:
- cpuCost 为左右孩子输出的数据大小之和,即行数*每行对应的 avgRowSize。注意:这个avgRowSize 统计的是经过 Column Prune 之后的列数对应的平均行大小。
- memoryCost 为右孩子的输出数据大小。做 HashJoin,右表为 Builder 表,占用内存,如果是 crossJoin 会计算对应的 Penalty(此处为10^8L)。
- networkCost 此处为 0,因为 HashJoin 本身不发生任何的网络交换。
参与采集、计算 Stats 相关的类为:
- CreateAnalyzeJobStmt,负责建立采集信息的异步 Schedule Job。
- AnalyzeStmt,手动 Analyze 命令搜集 Stats。
- StatisticAutoCollector,负责 Schedule 采集 Stats。
- StatisticsCalulator,真正的核心类,负责计算各种算子的 Statistics,在上文提到的 DeriveStatsTask 中调用。
**#05**
**Reference**
**—**
[1] https://www.cse.iitb.ac.in/infolab/Data/Courses/CS632/Papers/Cascades-graefe.pdf
[2] https://15721.courses.cs.cmu.edu/spring2017/papers/15-optimizer2/p337-soliman.pdf
[3]https://github.com/StarRocks/starrocks/tree/117716c899fe7649f0c88eedb75fa1621d6ef5f2/fe/fe-core/src/main/java/com/starrocks/sql/optimizer