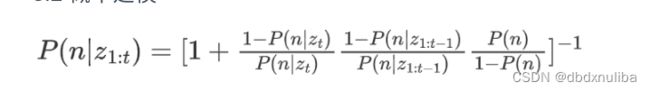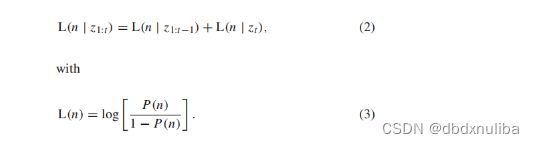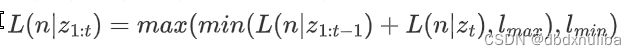2D栅格-3D八叉树地图及其概率更新
转载自:
2D栅格-3D八叉树地图及其概率更新_喂-你在楞什么的博客-CSDN博客_八叉树地图
2D栅格-3D八叉树地图及其概率更新
-
- 一.栅格/体素概率更新
-
- 1.占据栅格地图
-
- 1.1概率更新公式
- 1.2 二维坐标系到栅格索引的转化
- 2.八叉树地图
-
- 2.1八叉树原理
- 2.2概率更新公式
- 二.八叉树工程解析
-
- 1.Octomap基本数据类型解析
- octomap::Vector3
- octomap::OcTreeNode
- octomap::OcTreeKey
- octomap::KeySet
- octomap::KeyRay
- octomap::PointCloud
- octomap::OcTree
- 2.Octree下的常用函数
-
- 2.1 概率更新相关的几个重要参数设置函数
- 2.2 节点信息查询函数
- 2.3 世界坐标到体素格索引转换函数
- 2.4 节点概率更新函数
- 2.5 点云插入函数
- 2.6光线追踪函数
八叉树地图与占据栅格地图有很多相关之处!之前参加过icra比赛接触过占据栅格地图相关知识,正好一起整理一下!
由于项目需求撰写此文档,既是记录也是学习的过程。由于水平有限有些地方可能会出现错误,欢迎大家指正,发现后会及时改正!
另外对自己编写不规范可能会引起疑惑的地方在此说明:
1.文中提到的二维/三维的坐标系都是指的在不同维度下的世界坐标系,与之对应栅格/体素坐标系指的的是在把空间划分成一个个小单元后,对每一个小单元的索引。可以理解为对x,y,z三个不同方向的栅格数数,数他是第几个栅格并且记录下来。因此,栅格/体素坐标系一定是整数类型的,不存在第2.5个栅格这样的说法。由于边想边写所以有的地方想表达的是同一个东西但是称呼可能没有统一,特此说明文中所提到的栅格/体素坐标系=栅格/体素索引=地图中的坐标,以后会修改统一规范化。
一.栅格/体素概率更新
1.占据栅格地图
1.1概率更新公式
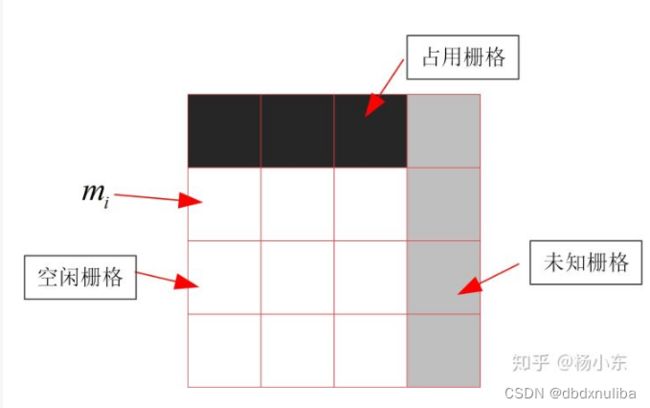
我们先从基础的【占据栅格地图】说起~~
写公式太复杂啦也没有什么直观感,所以手手写推导如下:


激光雷达的反演观测模型:
1.2 二维坐标系到栅格索引的转化
如何将真实世界中的坐标转化为栅格地图中的坐标呢
考虑一维的情况:
图中x xx是真实世界中的坐标,i ii为离散化了的地图(栅格地图)中的坐标,r rr为一格的长度,1 / r 1/r1/r表示分辨率,显然我们有:i = c e i l ( x / r ) i=ceil(x/r)i=ceil(x/r)。
同理,二维情况下:( i , j ) = ( c e i l ( x / r ) , c e i l ( y / r ) ) (i,j)=(ceil(x/r),ceil(y/r))(i,j)=(ceil(x/r),ceil(y/r))。
2.八叉树地图
2.1八叉树原理
八叉树即是有八个子节点的树,八块示意图如下图所示。实际的数据结构就是一个树根不断往下扩展,每分8个小枝,直到叶子为止。叶子节点代表了分辨率最高的情况。如分辨率为0.01cm,则每个叶子就是1cm见方的小方块。
八叉树的实现步骤如下:
(1).设定最大递归深度
(2).找出场景的最大尺寸,并以此尺寸建立第一个立方体
(3).依序将单位元元素丢入能被包含且没有子节点的立方体
(4).若没有达到最大递归深度,就进行细分八等份,再将该立方体所装的单位元元素全部分担给八个子立方体
(5).若发现子立方体所分配到的单位元元素数量不为零且跟父立方体是一样的,则该子立方体停止细分,因为跟据空间分割理论,细分的空间所得到的分配必定较少,若是一样数目,则再怎么切数目还是一样,会造成无穷切割的情形。
(6) 重复3,直到达到最大递归深度。
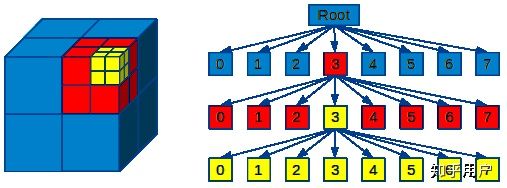
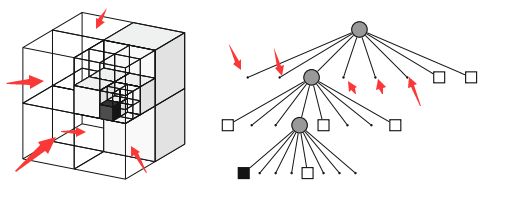
在Octomap库中实现的octomap::OcTree对于空间的划分方式如下图所示:
如图所示,体素格坐标系即体素格索引的原点在正方体左上角(图中的0位置处),那么该体素格0在体素格坐标系下的坐标即为原点(0,0,0),在图中用红色字体000表示。既然是对空间进行划分,那么肯定有个先后顺序,经过测试在Octomap库中的划分方式为:从上至下从左至右划分。也就是按图中0→1→2→···→7的方式进行划分。
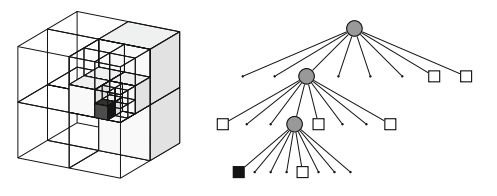
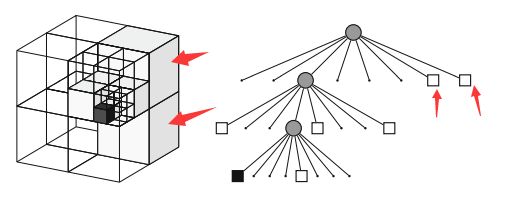
特别注意的是,节点的展开只有可能是0个或者8个子节点,因此一旦展开顺序就固定了,可能展开后的八个节点中只有第三节点有值,那也需要按照顺序存放,0到2节点指针为空。这样划分后的结果如下图所示:
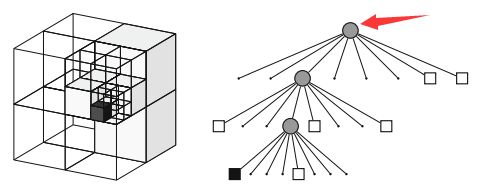
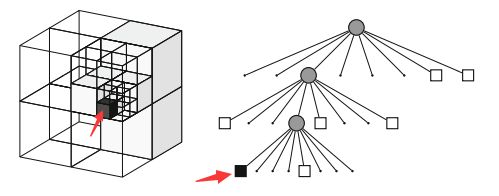
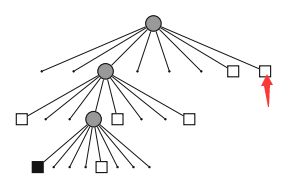
对于划分好的八叉树地图,每个小方块都有一个描述它是否被占据的数,通常用0-1之间的浮点数表示它被占据的概率,0.5表示未确定,越大表示被占据的可能性越高。下图是一棵八叉树:
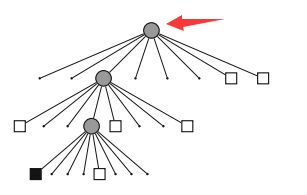
用树结构的好处是:当某个节点的子结点都“占据”或“不占据”或“未确定”时,就可以把它(节点)给剪掉!换句话说,如果没必要进一步描述更精细的结构(子节点)时,我们只要一个粗方块(父节点)的信息就够了。这可以省去很多的存储空间。不用存一个“全八叉树”!
2.2概率更新公式
在八叉树中,我们同样也用概率来表达一个叶子是否被占据,并且栅格地图中对于一格栅格概率的推导完全和在三维世界中对于一
二.八叉树工程解析
1.Octomap基本数据类型解析
-
octomap::Vector3
Vector3这个数据结构给我们提供了octomap命名空间下自定义的的三维向量表达,它可以表达三维空间中的一个平移向量,也可以表达以欧拉角形式表示的三维物体,还提供了多个与向量运算相关的函数,例如相对于坐标系的变换实现函数、向量归一化函数、向量点积函数等。
float data [3]
一般程序中使用的是 point3d的数据类型,是Octomap自定义的类型别名,原始的数据结构还得查看octomath::Vector3
typedef octomath::Vector3 octomap::point3d
-
octomap::OcTreeNode
AbstractOcTreeNode ** children
float value
OcTreeNode为在八叉树中使用的节点类。有一个数据域和一个指针域(指向一个数组里面存放的子节点的指针)。“value”存储体素单元格的对数概率log O d d ( s ) \log Odd(s)logOdd(s)。
-
octomap::OcTreeKey
OcTreeKey 是用于内部键寻址的容器类。内部储存了在三维空间下从原点开始到某一体素格的离散地址。类似于栅格地图中的栅格序号的概念。这个数据结构是一个关键字,它可以实现对八叉树节点OcTreeNode的关键字查询。
OcTreeKey定义的成员变量:
key_type k [3]
其中key_type是一个类型别名
typedef uint16_t octomap::key_type
-
octomap::KeySet
typedef unordered_ns::unordered_set octomap::KeySet
KeySet是Octomap自定义的类型别名!它使用一个无序关联容器(std::unordered_set/boost::unordered_set)来存储一组关键字集合,由哈希函数来组织哈希表。
哈希函数也称散列函数,直观上,它是一个映射函数f ff,实现的功能为:内存中记录的存储位置=f ( 关 键 字 ) f(关键字)f(关键字)。在Octomap中,关键字对应的哈希值由KeyHash结构体实现,该结构体存在octomap::OcTreeKey类中。
// OcTreeKey::KeyHash: Provides a hash function on Keys
struct KeyHash
{
size_t operator()(const OcTreeKey& key) const{
// a simple hashing function
// explicit casts to size_t to operate on the complete range
// constanst will be promoted according to C++ standard
//哈希函数:
return size_t(key.k[0]) + 1447*size_t(key.k[1]) + 345637*size_t(key.k[2]);
}
};
-
octomap::KeyRay
typedef std::vector< OcTreeKey >::const_iterator const_iterator
typedef std::vector< OcTreeKey >::iterator iterator
typedef std::vector::reverse_iterator reverse_iterator;
**KeyRay**是octomap自定义的类型别名。
KeyRay内部以下成员:
private:
std::vector ray;
std::vector::iterator end_of_ray;
const static size_t maxSize = 100000;
实际使用时,KeyRay在自身成员变量ray中保存单条光束在三维空间中raytracing(光线追踪)的结果。在Octomap工程文件OctomapServer.h中的描述也可以体现这一点:
//OctomapServer.h
...
octomap::KeyRay m_keyRay; // temp storage for ray casting ----光线追踪的临时容器
...
那么现在如果我们想整合每一条光束得到的结果,那么就不能用这个临时容器进行存储了,我们采用KeySet数据格式也就是一个关键字的集合来收纳所有光束(也即点云数据)raytracing的结果。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2C1qcRg9-1630489238187)(/home/zyc/.config/Typora/typora-user-images/image-20210805171639204.png)]
-
octomap::PointCloud
3D 坐标集合 (point3d)
在数据结构的设计上,它包括了两个受保护的成员变量:
pose6d current_inv_transform
point3d_collection points
其中
typedef std::vector octomap::point3d_collection
这里,points变量又是一个自定义的类型别名,可以看出octomap::PointCloud使用了vector容器保存点云数据。于是,很自然的在程序中需要从PCL点云数据中提取Octomap点云数据结构时,可以使用push_back压入数据。
-
octomap::OcTree
在上面将Octomap最基本的数据类型全部列出并加以解释,却唯独还没有解释八叉树类型OcTree的数据结构。可以认为OcTree八叉树类是建立在以上所有数据结构基础上的顶层类,并不是指其它所有类型都派生于它,而是它提供了操作以上所有数据结构的的方法(函数),也就是核心的函数都由八叉树类型OcTree中提供。
![]()
- tree_iterator
遍历完整树(内部节点和叶子)的迭代器。可通过迭代器的类内函数访问当前迭代器访问节点的各种数据。示例如下:
for (OcTree::tree_iterator it = tree.begin_tree(),end = tree.end_tree(); it != end; ++it) {
std::cout << "当前树深度为 Node depth: " << it.getDepth() << std::endl;
std::cout << "当前体素的中点坐标 Node center: " << it.getCoordinate() << std::endl;
if(tree.coordToKeyChecked(it.getCoordinate(),key))
{ cout<<"点的坐标转换树内体素的索引为:("<getValue() << std::endl;
std::cout << "Node Occupancy Probability: " << it->getOccupancy() << std::endl;
std::cout << "Node LogOdds: " << it->getLogOdds() << '\n' << std::endl;
}
2.Octree下的常用函数
以下列举出本人所遇到的常用的函数供以后参考学习,特别指出列举出的函数都有着各种方式的重载版本,可点击函数名链接去官方API文档进行查看。
2.1 概率更新相关的几个重要参数设置函数
| void | setProbHit (double prob) |
|---|---|
| void | setProbMiss (double prob) |
这两个函数决定了inverse sensor model(反演观测模型)的概率log O d d \log OddlogOdd更新的具体参数,默认情况下占据体素被击中(Hit)的概率值为0.7,对应的log O d d \log OddlogOdd为0.847298,空闲体素被穿越(traverse)的概率值为0.4,对应的log O d d \log OddlogOdd为-0.405465。
| double | getProbHit () const |
|---|---|
| float | getProbHitLog () const |
| double | getProbMiss () const |
| float | getProbMissLog () const |
可以调用getProHit/getProHitLog、getProMiss/getProMissLog查看默认的参数设定。
| void | setClampingThresMax (double thresProb) |
|---|---|
| void | setClampingThresMin (double thresProb) |
这两个函数决定了一个体元执行log O d d \log OddlogOdd更新的阈值范围。也就是说某一个占据体素的概率值爬升到0.971(对应的log O d d \log OddlogOdd为3.5)或者空闲体素的概率值下降到0.1192(对应的log O d d \log OddlogOdd为-2)便不再进行log O d d \log OddlogOdd更新计算。对应了之前概率更新时所说的最大最小值的限制。
| double | getClampingThresMax () const |
|---|---|
| float | getClampingThresMaxLog () const |
| double | getClampingThresMin () const |
| float | getClampingThresMinLog () const |
可以调用getClampingThresMax/getClampingThresMaxLog、getClampingThresMin/getClampingThresMinLog查看默认的参数设定。
这个函数定义了octomap判定某一个体素属于占据状态的阈值(isNodeOccupied函数),默认是0.5,网上所说一般情况下将其设定为0.7。
2.2 节点信息查询函数
传入参数为一个point3d类型的三维点对象,如果在这个地图tree中,这个三维点对应的位置有节点(不管占用与否),那么将返回该位置的节点指针,否则将返回一个空指针;
2.3 世界坐标到体素格索引转换函数
函数实现带有边界检查,返回参数为在上文介绍过的指向OcTreeKey类型的内部键寻址的容器类地址,传入参数为一个point3d类型的三维点对象,如果在这个地图tree中,将返回这个三维点对应的体素格的关键字,如果不在这个地图中则返回false。
2.4 节点概率更新函数
举个例子:
point3d endpoint( 4.09f, 4.09f, 4.09f );
tree.updateNode( endpoint, true );
这两行代码,由于分辨率是0.1,并不能精确到0.01,所以要把这个(4.09,4.09,4.09)归到(4.0,4.0,4.0)这个节点。
之前也介绍过对于程序默认来说Occupancy probability最大值为0.971,最小值为0.1192,我们可以根据自己的需求设置最大最小值。
2.5 点云插入函数
插入点云。相当于批量操作updateNode,地图中的每个体素只更新一次,占用节点优先于空闲节点。需要sensor_origin坐标(就是传感器在全局坐标系下的xyz)。
2.6光线追踪函数
光线从“原点origin”以给定方向投射,光线第一个碰到的占据单元的中心坐标存入参数end返回。 如果原点本身被占用或未知则返回本身。
如果光线投射击中了一个被占用的节点,castRay() 将返回 true。 如果光线投射返回 false,可以通过 search() 函数查看返回的end 处的节点是否是未知单元。
castRay函数中参数origin(光束起点)是世界坐标系下激光雷达的位置;参数direction也就是光束的方向向量,只需要给出sensor model光线的方向向量即可,且没有必要对方向向量归一化,castRay函数在内部会为我们完成这件事,返回的光束末端点end是世界坐标系下的坐标表达。
从起点到(不包括)终点跟踪光线,返回光束穿过的所有节点的 OcTreeKey。参数origin(光束起点)和参数end(传感器末端击中点)都是世界坐标系下的坐标!
简单谈谈八叉树地图环境构建_一头小学牲的博客-CSDN博客_八叉树地图
原文我是放在Notion上的,见这个地方
八叉树是干什么的?
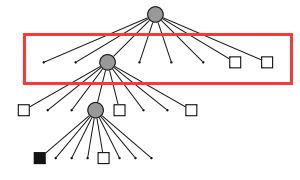
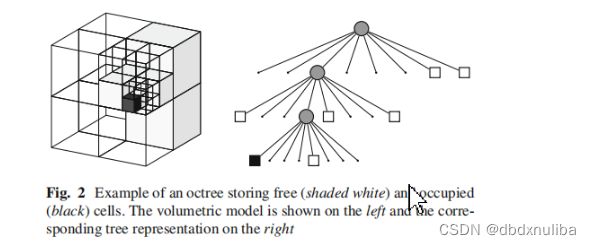
八叉树是一种构建环境地图的方法,顾名思义,就是以八叉树的形式来对环境进行建模。下图是一个八叉树表示环境的例子,左图表示构建的环境,右图表示该环境对应的组织形式。看不懂没关系,下面我们将对八叉树进行详细地讲解。
八叉树的基本思想
八叉树的基本思想是,递归地把空间分成八个方块,这些方块在内存中以八叉树的形式组织起来,而每个树的节点对应于空间中的一个方块。我们用一个0~1之间的浮点数来描述这个节点被(障碍物)占据的概率,0表示未占据,1表示空闲,0.5表示不确定。当某个节点下的所有子节点的概率都是相同的时候(如都被占据,都是空闲或都是不确定),我们可以将这些子节点通过剪枝修剪掉,只保留父节点,从而节省内存。相对于点云而言,八叉树是一种高效的环境建模方法,大大地减少了内存占用。
说到这里,大家可能对图1的含义有一点粗糙的认识了,其中,根节点对应于最大的立方体,下面八个子节点表示被划分出的八个方块。
这些灰色的方块对应于树中的白色正方形,表示空闲。
被进一步递归划分的方块对应于树中的灰色圆,表示有内节点,也就是说,它子节点的概率不是都相等的。
节点的概率
八叉树的数据结构
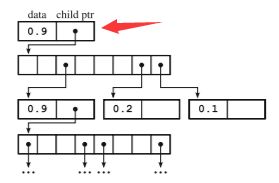
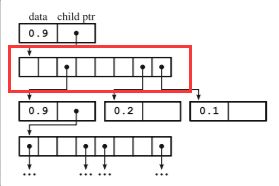
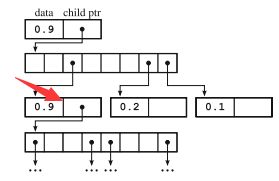
下图表示图1所示八叉树对应的存储结构,一个节点由data域和孩子指针域构成,其中data就是节点的Logit值,如果一个节点有内节点,那么该节点的指针域指向一个指针数组,这个指针数组分别又指向对应的节点。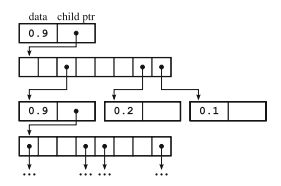
八叉树的压缩
写不动了,下次再写
To be continue
参考文献
- OctoMap: An efficient probabilistic 3D mapping framework based on octrees
- 2D栅格-3D八叉树地图及其概率更新_喂-你在楞什么的博客-CSDN博客 (这篇文章的数学推导讲的比较详细)
- octomap的入门与学习_qq_42424625的博客-CSDN博客
- 游戏场景管理的八叉树算法是怎样的? - 知乎 (zhihu.com)
- SLAM拾萃(1):octomap - 半闲居士 - 博客园 (cnblogs.com)
- 从logit变换到logistic模型_帅帅de三叔-CSDN博客_logit变换
- 优势比_百度百科 (baidu.com)
视觉十四讲:第十二讲_八叉树地图 - penuel - 博客园
OctoMap 论文笔记 – 风林轩
论文链接
- OctoMap: an efficient probabilistic 3D mapping framework based on octrees
-
OctoMap中文翻译版
1. 论文概要
- 提出一个生成3D环境模型,映射方法基于 八叉树 ,使用 概率估计
- 提出一种 八叉树 压缩算法,以保证三维模型的紧凑
- 三个重要的要求
- 概率表示
- 未映射区域的建模
- 效率
2. 方法对比
- 立方体网格(体素)法:
- 缺点就是内存需求大,非常大
- 点云方法:
- 既不模拟自由空间,也不模拟未知区域,不能直接处理传感器噪声和动态对象
- 仅适用于静态环境中的高精度传感器,且不需表示位置区域
- 内存消耗无上限
-
2.5D地图:
- 不以体积表示环境,地图不表示实际环境
- 在改进后也需要预先知道地图范围,更新更加复杂并且没有多分辨能力
- 后续的映射不能更新细分现有卷,导致模型不正确
- 八叉树:
- 延迟了映射卷的初始化,直到需要集成测量为止
- 该论文提出的方法解决了 映射压缩或映射中的有节置信度的问题
3. 具体内容框架
3.1 八叉树
- 八叉树中的每个节点表示立方体卷中包含的空间,即体素
-
递归细分改卷为八个子卷,直到到达给定的最小的体素大小
-
布尔设置:
- 明确所有的自由卷
-
紧凑操作
-
如果节点中的所有子节点具有相同的状态,则可以对于其进行修剪,减少需要维护的树中的节点数
-
数据访问的复杂度方面
-
限定八叉树的最大深度 D_{max}Dmax , 则随机节点的查找复杂度为常数
3.2 概率建模
- 设置阈值,当达阈值时,认为体素被占用,否则认为其为自由的
-
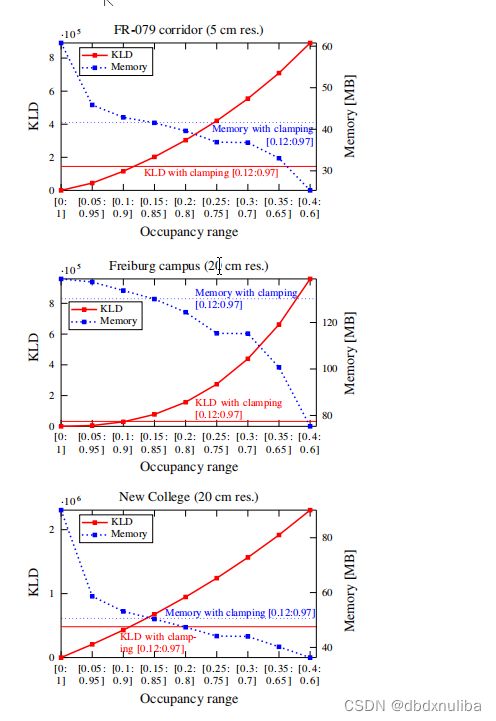
利用钳位更新的策略定义占用概率的上下限
-
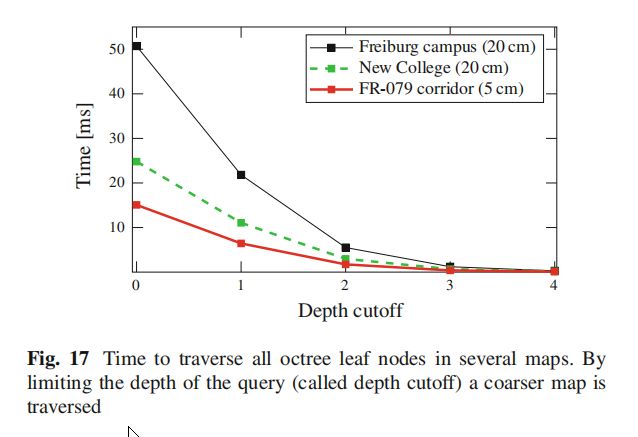
多种分辨率查询
对内部节点实现多分辨率查询。当遍历到一个给定深度(非叶节点深度)时,对其进行更粗略的分割
3.3 八叉树压缩
- 原因:传感器噪声和离散化误差可能导致不同的概率,从而干扰依赖于相同节点信息的压缩方案
- 解决方法:钳位更新,每当体素的log-oddslog−odds 值达到 l_{min},l_{max}lmin,lmax ,即视为节点在方法中时稳定的
4. 实现细节
4.1 高效内存的实现
4.2 地图文件生成
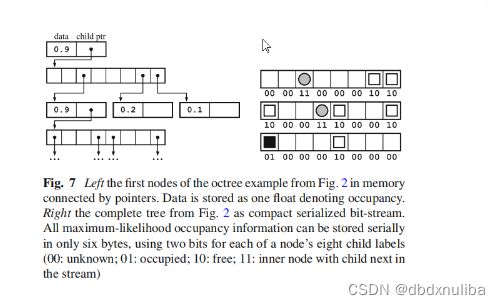
- 将八叉树中的各个状态递归地编码成为紧凑的比特流中(叶子节点不必添加,可以在解码过程中重构)
- 每一行具有对应于根节点上行的节点。
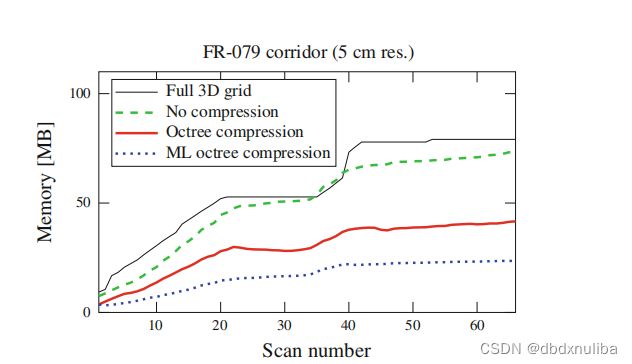
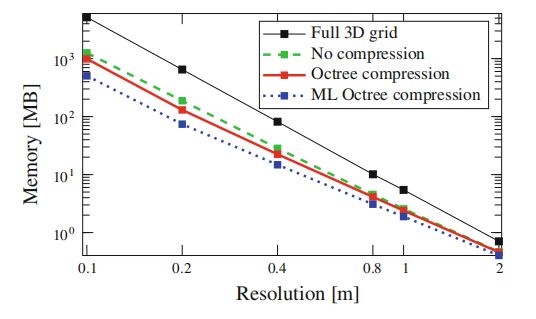
5. 实验结果
6.个人观点
6.1 创新点
- 运用了压缩剪枝的方法,减少了内存的使用
- 支持多分辨率映射查询
- 使用钳位更新来压缩八叉树
- 八叉树映射为比特流来减少内存
6.2 不足之处
- 在传感器接收到较少的光束时,限制传感器范围没有明显的加速
- 在映射置信度和压缩之间存在权衡