经典卷积神经网络

目录

一、 卷积神经网络的演变

二、经典神经网络

2.1 LeNet5

2.1.1 背景

2.1.2 结构

2.1.3 总结

2.2 AlexNet

2.2.1 背景

2.2.2 创新点

2.2.3 结构

2.3 VGG-16

2.3.1 背景

2.3.2 结构

2.4 Inception Net

2.4.1 背景

 2.4.2 结构

2.5 ResNet（残差神经网络）

 2.5.1 背景

2.5.2 梯度消失和梯度爆炸

 2.5.3 ResNet的核心

2.5.4 ResNet的结构

2.6 DenseNet （密集网络）

2.6.1 背景

 2.6.2 特点

2.6.3 结构

​编辑 2.6.4 优点

三、 R-CNN系列

3.1 背景

3.2 实现过程

3.2.1 Selective Search算法

3.2.2 SVM分类

3.2.3 Bbox回归

3.3 其他R-CNN系列网络

---

一、 卷积神经网络的演变

二、经典神经网络

2.1 LeNet5

2.1.1 背景

Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, November 1998.

LeNet5是由Y.LeCun等人提出的，主要进行手写数字识别和英文字母识别。

很经典，虽然小，但是模块齐全。

2.1.2 结构

1. 输入层

        32X32的图片

2. C1层（卷积层）

        采用了6个5X5的卷积核，且步长为1（32-5+1 = 28）得到了6个28X28的特征图。此时神经元个数为6X28X28 = 784 个。

3. S2层（下采样层）

        进行了平均池化，池化核2X2，步长为2（无重叠移动），得到6个14X14的特征图。平均池化后加乘一个权重，加上一个偏置作为激活函数的输入，激活函数的输出作为下一层的输入。

4. C3层

        采用了16个5X5的卷积核组，且每个卷积核组中卷积核数量不同（前6个卷积核个数为3，中间6个为4，之后3个为4，最后一个为4），如下图所示：

 

         加偏置和激活函数后得到16个10X10的特征图（14-5+1 = 10），此时神经元数量为1600。

        此处有个疑问，为什么要设计卷积核组中卷积核数量不同？应该是有助于减少参数数量，降低模型复杂度。

5. S4层

        对16个10X10的特征图进行池化核为2X2，步长2的最大池化，得到的最大值乘以一个权重参数，再加上一个偏置参数作为激活函数（sigmoid）的输入，得到16张 5*5的特征图，神经元个数已经减少为16*5*5=400。

6. C5层

        用16个5*5的卷积核进行卷积，乘以一个权重参数并求和， 再加上一个偏置参数作为激活函数 （sigmoid）的输入，得到1*1（5- 5+1=1）的特征图。

         然后我们希望得到120个特征图，就要用总共120个5*5卷积核组（每个组16 个卷积核）进行卷积，神经元减少为 120个。

        与C3层不同的是，这里的连接是一种全连接。

 7. F6层

        全连接层，有84个节点，对应的是一个7X12的比特图，如下所示：

         特征图大小与C5一样都是1×1，与C5层全连接。计算输入向量和权重向量之间的点积，再加上一个偏置，然后将其传递给sigmoid 函数得出结果。

 8.Output层（全连接层）

        共有10个节点，分别代表数字0到9， 如果节点i的输出值为0（比如向量为[0,1,1,1,...1],识别为数字0)，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式。

        假设x是上一层的输入（F6层的84个神经元），y是RBF的输出，则RBF输出的计算方式是：

         的值由i的比特图编码确定，i从0到9，j取值从0到84-1。 RBF输出的值越接近于0，表示当前网络输入的识别结果与字符i 越接近。

2.1.3 总结

        卷积核大小、卷积核个数（特征图需要多少个）、池化核大小和步长等这些参数都是变化的，这就是所谓的CNN调参，需要学会根据需要进行不同的选择 。

        后续补上LeNet5识别首先数字的代码。

2.2 AlexNet

2.2.1 背景

        获得ImageNet LSVRC-2012（物体识别挑战赛）的冠军，1000 个类别120万幅高清图像，Error: 26.2%(2011)→15.3%(2012)。

        AlexNet确定了CNN在计算机视觉领域的王者地位。     

A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012   

2.2.2 创新点

• 首次成功应用ReLU作为CNN的激活函数。
• 使用Dropout丢弃部分神元，避免了过拟合。
• 使用重叠MaxPooling（让池化层的步长小于池化核的大小），一 定程度上提升了特征的丰富性。
• 使用CUDA加速训练过程。
•  进行数据增强，原始图像大小为256×256的原始图像中重复截取 224×224大小的区域，大幅增加了数据量，大大减轻了过拟合， 提升了模型的泛化能力。

2.2.3 结构

AlexNet论文中的原始结构分成了两组，并不是所有通道都用来卷积，如下图所示：

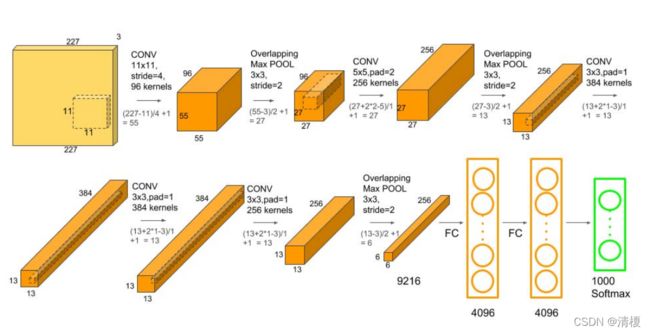
 后来更常用的结构是不分组，而是全部进行卷积，结构图如下所示 ：

 AlexNet可分为8层（池化层算入卷积层中），5个卷积层，3个全连接层。介绍时按照常用不分组的结构进行介绍。

1. 输入层

        227X227X3的图像作为输入

2. 第一层（卷积层）

        使用96个11X11的卷积核，步长为4，进行卷积，输出为55X55X96（(227-11)/4+1 = 55)。

        然后使用核大小3X3，步长为2（可以重叠）的最大池化，输出为27X27X96（(55-3)/2+1=27)

3. 第二层（卷积层）

        使用256个大小为5×5的卷积核，步长为1，同时利用padding保证输出尺寸不变（pad=2），因此该层输出大小为27×27×256（27+2*2-5+1）。

        然后再通过核大小为3×3、步长为2的最大池化层，进而输出大小为13×13×256((27-3）/2+1=13)。

4. 第三层与第四层（卷积层）

        使用384个大小为3X3的卷积核，步长为1，进行same卷积，输出为13X13X384。

5. 第五层（卷积层）

        使用256个大小为3X3的卷积核，步长为1，进行same卷积，输出为13X13X256。

        然后再通过核大小为3X3、步长为2的最大池化层，进而输出为6X6X256，并进行数据扁平化，展开为9216个单元。

6. 第六、七、八层（全连接层）

        全连接加上Softmax分类器输出1000类的分类结果。

2.3 VGG-16

2.3.1 背景

        VGGNet由剑桥大学和DeepMind公司提出。比较常用的是VGG-16，结构规整，具有很强的拓展性。

        相较于AlexNet，VGG-16网络模型中的卷积层均使用3*3的卷积核，且均为步长为1的same卷积，池化层均使用2*2的池化核，步长为2。

K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.

2.3.2 结构

        整体网络结构如下图所示。卷积层均为3X3，步长1的same卷积，池化层均为2X2，步长2的最大池化。共有13个卷积层、3个全连接层，共16层，故称之为VGG-16。

	Conv1	Conv2	Conv3	Conv4	Conv5
卷积层数	2	2	3	3	3
卷积核数	64	128	256	512	512

此处有个疑问，为什么要设计成这种多卷积层串联且卷积核小的结构？

        因为两个卷积核大小为3X3的卷积层串联后的感受野尺寸为5X5，相当于单个卷积核大小为5X5的卷积层。 两者参数数量比值为(2*3*3)/(5*5)=72% ，前者参数量更少。 可以起到减少参数数量简化模型的作用。

        此外，两个的卷积层串联可使用两次ReLU激活函数，而一个卷积层只使用一次。

2.4 Inception Net

2.4.1 背景

        Google公司2014年提出。

        文章提出获得高质量模型最保险的做法就是增加模型的深度（层数）或者是其宽度（层核或者神经元数），采用了22层网络。

以下为Inception四个版本所对应的论文，末尾为ILSVRC中的Top-5错误率：

• [v1] Going Deeper with Convolutions: 6.67% test error
• [v2] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift: 4.8% test error
• [v3] Rethinking the Inception Architecture for Computer Vision: 3.5% test error
• [v4] Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning: 3.08% test error

 2.4.2 结构

和卷积层、池化层顺序连接的结构（如VGG网络）相比，这样的结构主要有以下改进：

1. 一层block就包含1x1卷积，3x3卷积，5x5卷积，3x3池化(使用这样的尺寸不是必需的，可以根据需要进行调整)。这样，网络中每一层都能学习到“稀疏”（3x3、5x5）或“不稀疏”（1x1）的特征，既增加了网络的宽度，也增加了网络对尺度的适应性；
2. 通过deep concat在每个block后合成特征，获得非线性属性。

 同时在3X3、5X5卷积核之前加上1X1的卷积核，来降低特征图的厚度，如下图所示：

 更详细的介绍见：卷积神经网络结构简述（二）Inception系列网络 - 知乎

2.5 ResNet（残差神经网络）

 2.5.1 背景

        ResNet（Residual Neural Network），又叫做残差神经网络，是由微软研究院的何凯明等人2015年提出。

        获得CVPR2016最佳论文奖。

        残差神经网络的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “快捷连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。神经网络的“深度”首次突破了100层、最大的神经网络甚至超过了1000层。

Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Deep Residual Learning for Image Recognition. CVPR 2016: 770-778

2.5.2 梯度消失和梯度爆炸

         随着卷积网络层数的增加，误差的逆传播过程中存在的梯度消失和梯度爆炸问题同样也会导致模型的训练难以进行。 甚至会出现随着网络深度的加深，模型在训练集上的训练误差会出现先降低再升高的现象。 残差网络的引入则有助于解决梯度消失和梯度爆炸问题。

梯度消失和梯度爆炸的原因详解：

详解机器学习中的梯度消失、爆炸原因及其解决方法_Double_V_的博客-CSDN博客_梯度消失的原因及解决方法

 2.5.3 ResNet的核心

        ResNet的核心是叫做残差块（Residual block）的小单元，残差块可以视作在标准神经网络基础上加入了跳跃连接（Skip connection），如下图所示。跳跃连接增强了前面数据对于l+2的影响，可以有效减小梯度消失。

        按照这个思路，ResNet分别构建了带有跳跃连接的ResNet构建块、以及降采样的ResNet构建块，降采样构建块的主杆分支上增加了一个1×1的卷积操作，如下图所示：

2.5.4 ResNet的结构

        下图展示了34层ResNet模型的架构图，仿照AlexNet的8层网络结构，也将ResNet划分成8个构建层（Building Layer）。一个构建层可以包含一个或多个网络层、以及一个或多个构建块（如ResNet构建块）。

        第一个构建层，由1个普通卷积层和最大池化层构建。

        第二个构建层，由3个残差模块构成。

        第三、第四、第五构建层，都是由降采样残差模块开始，紧接着3个、5个、2个残差模块。

2.6 DenseNet （密集网络）

2.6.1 背景

Gao Huang, Zhuang Liu, Laurens van der Maaten. Densely Connected Convolutional Networks. CVPR 2017

 2.6.2 特点

        相比ResNet，DenseNet提出了一个更激进的密集连接机制：即互相连接所有的层，具体来说就是每个层都会接受其前面所有层作为其额外的输入。在DenseNet中，每个层都会与前面所有层在channel维度上连接（concat）在一起，并作为下一层的输入。对于一个L层的网络，DenseNet共包含L（L+1）/ 2个连接。连接图如下图所示：

2.6.3 结构

        CNN网络一般要进行池化来降低特征图的大小，而DenseNet的密集连接方式需要特征图大小保持一致。为了解决这个问题，DenseNet网络中使用DenseBlock+Transition的结构。其中DenseBlock是包含很多层的模块，每个层的特征图大小相同，层与层之间采用密集连接方式。而Transition模块是连接两个相邻的DenseBlock，并且通过Pooling使特征图大小降低。

 2.6.4 优点

        DenseNets可以自然地扩展到数百个层，而没有表现出优化困难。

        在实验中，DenseNets随着参数数量的增加，在精度上产生一致的提高，而没有任何性能下降或过拟合的迹象。

        缓解了消失梯度问题。加强了特征传播，鼓励特征重用。

三、 R-CNN系列

3.1 背景

        Region-CNN的缩写，主要用于目标检测。  来自2014年CVPR论文“Rich feature hierarchies for accurate object detection and semantic segmentation”。

        在 Pascal VOC 2012 的数据集上，能够将目标检测的验证指标 mAP 提升到 53.7%，这相对于之前最好的结果提升了整整 13.3%。

3.2 实现过程

        • 区域划分：给定一张输入图片，从图片中提取 2000 左右类别独立的候选区域，采用的是 Selective Search 算法。

        • 特征提取：对于每个区域利用 CNN 抽取一个固定长度的特征向量， R-CNN 使用的是 Alexnet。

         • 目标分类：对每个区域利用 SVM 进行目标分类。

         • 边框回归：Bounding box Regression（Bbox回归)进行边框坐标偏移优化和调整。

3.2.1 Selective Search算法

核心思想：图像中物体可能存在的区域应该有某些相似性或者连续性，基于这一想法进行子区域合并。

首先，通过图像分割算法将输入图像分割成许多小的子区域。

其次，根据这些子区域之间的相似性(主要考虑颜色、纹理、 尺寸和空间交叠4个方面的相似性) 进行区域迭代合并。每次迭代过程中对这些合并的子区域做bounding boxes(外切矩形)， 这些子区域的外切矩形就是通常所说的候选框。

3.2.2 SVM分类

        在这里每个类别对应一个SVM分类器，如果有20个类别，则会有20SVM分类器。对于每个类别的分类器只需要判断是不是这个类别的，如果同时多个结果为Positive则选择概率之最高的。

3.2.3 Bbox回归

        核心思想是通过平移和缩放方法对物体边框进行调整和修正。

 给定，寻找一种映射f ，使得:

        

先做平移：

         

再做缩放：

真实偏移量：

计算损失函数：

         

 是输入目标的特征向量（AlexNet第五层pooling输出的特征）。

3.3 其他R-CNN系列网络

        具体如下所示，不进行详述